15.2 Exact Ruin Probabilities in Infinite Time

In order to present a ruin probability formula we first use the relation (15.1) and express $ L$ as a sum of so-called ladder heights. Let $ L_{1}$ be the value that the process $ \{S_{t}\}$ reaches for the first time above the zero level. Next, let $ L_{2}$ be the value which is obtained for the first time above the level $ L_{1}$; $ L_{3},L_{4},\ldots $ are defined in the same way. The values $ L_{k}$ are called ladder heights. Since the process $ \{S_{t}\}$ has stationary and independent increments, $ \{L_k\}_{k=1}^\infty$ is a sequence of independent and identically distributed variables with the density

$\displaystyle f_{L_1}(x)=\bar{F}_{X}(x)/\mu.$ (15.6)

One may also show that the number of ladder heights $ K$ is given by the geometric distribution with the parameter $ q=\theta/(1+\theta)$. Thus, the random variable $ L$ may be expressed as

$\displaystyle L=\sum_{i=1}^{K}L_{i}$ (15.7)

and it has a compound geometric distribution. The above fact leads to the Pollaczek-Khinchin formula for the ruin probability:

$\displaystyle \psi(u)=1-\textrm{P}(L\leq u)=1-\frac{\theta}{1+\theta}\sum_{n=0}^{\infty} \left(\frac{1}{1+\theta}\right)^{n}F^{\ast n}_{L_1}(u),$ (15.8)

where $ F^{\ast n}_{L_1}(u)$ denotes the $ n$th convolution of the distribution function $ F_{L_1}$.

One can use it to derive explicit solutions for a variety of claim amount distributions, particularly those whose Laplace transform is a rational function. These cases will be discussed in this section. Unfortunately, heavy-tailed distributions like e.g. the log-normal or Pareto one are not included. In such a case various approximations can be applied or one can calculate the ruin probability directly via the Pollaczek-Khinchin formula using Monte Carlo simulations. This will be studied in Section 15.3.

We shall now, in Sections 15.2.1-15.2.4, briefly present a collection of basic exact results on the ruin probability in infinite time. The ruin probability $ \psi(u)$ is always considered as a function of the initial capital $ u$.


15.2.1 No Initial Capital

When $ u=0$ it is easy to obtain the exact formula:

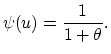$\displaystyle \psi(u)=\frac{1}{1+\theta}.$    

Notice that the formula depends only on $ \theta$, regardless of the claim frequency rate $ \lambda $ and claim size distribution. The ruin probability is clearly inversely proportional to the relative safety loading.


15.2.2 Exponential Claim Amounts

One of the historically first results on the ruin probability is the explicit formula for exponential claims with the parameter $ \beta$, namely

$\displaystyle \psi (u) = \frac{1}{1+\theta}\exp\left(-\frac{\theta \beta u}{1+\theta}\right).$ (15.9)

In Table 15.2 we present the ruin probability values for exponential claims with $ \beta =6.3789\cdot 10^{-9}$ (see Chapter 13) and the relative safety loading $ \theta=30\%$ with respect to the initial capital $ u$. We can observe that the ruin probability decreases as the capital grows. When $ u=1$ billion USD the ruin probability amounts to $ 18\%$, whereas $ u=5$ billion USD reduces the probability to almost zero.


Table 15.2: The ruin probability for exponential claims with $ \beta =6.3789\cdot 10^{-9}$ and $ \theta =0.3$ ($ u$ in USD billion).
$ u$ 0 $ 1$ $ 2$ $ 3$ $ 4$ $ 5$  
               
$ \psi(u)$ 0.769231 0.176503 0.040499 0.009293 0.002132 0.000489  
               

24050 STFruin02.xpl


15.2.3 Gamma Claim Amounts

Grandell and Segerdahl (1971) showed that for the gamma claim amount distribution with mean $ 1$ and $ \alpha\leq 1$ the exact value of the ruin probability can be computed via the formula:

$\displaystyle \psi (u) = \frac{\theta(1-R/\alpha)\exp(-Ru)}{1+(1+\theta)R-(1+\theta)(1-R/\alpha)}+ \frac{\alpha\theta \sin(\alpha\pi)}{\pi}\cdot I,$ (15.10)

where

$\displaystyle I = \int_{0}^{\infty}\frac{x^{\alpha}\exp\left\{-(x+1)\alpha u\ri... ...ha(1+\theta)(x+1)\right\}-\cos(\alpha\pi)\right ]^{2}+\sin^{2}(\alpha\pi)}\;dx.$ (15.11)

The integral $ I$ has to be calculated numerically. We also notice that the assumption on the mean is not restrictive since for claims $ X$ with arbitrary mean $ \mu$ we have that $ \psi_{X}(u)=\psi_{X/\mu}(u/\mu)$. As the gamma distribution is closed under scale changes we obtain that $ \psi_{G(\alpha,\beta)}(u)=\psi_{G(\alpha,\alpha)}(\beta u/\alpha)$. This correspondence enables us to calculate the exact ruin probability via equation (15.10) for gamma claims with arbitrary mean.

Table 15.3 shows the ruin probability values for gamma claims with with $ \alpha =0.9185$, $ \beta =6.1662\cdot 10^{-9}$ (see Chapter 13) and the relative safety loading $ \theta=30\%$ with respect to the initial capital $ u$. Naturally, the ruin probability decreases as the capital grows. Moreover, the probability takes similar values as in the exponential case but a closer look reveals that the values in the exponential case are always slightly larger. When $ u=1$ billion USD the difference is about $ 1\%$. It suggests that a choice of the fitted distribution function may have a an impact on actuarial decisions.


Table 15.3: The ruin probability for gamma claims with $ \alpha =0.9185$, $ \beta =6.1662\cdot 10^{-9}$ and $ \theta =0.3$ ($ u$ in USD billion).
$ u$ 0 $ 1$ $ 2$ $ 3$ $ 4$ $ 5$
             
$ \psi(u)$ 0.769229 0.174729 0.039857 0.009092 0.002074 0.000473
             

24146 STFruin03.xpl


15.2.4 Mixture of Two Exponentials Claim Amounts

For the claim size distribution being a mixture of two exponentials with the parameters $ \beta_1$, $ \beta_2$ and weights $ a$, $ 1-a$, one may obtain an explicit formula by using the Laplace transform inversion (Panjer and Willmot; 1992):

$\displaystyle \psi (u) = \frac{1}{(1+\theta)(r_{2}-r_{1})}\left \{(\rho-r_{1})\exp (-r_{1}u)+ (r2-\rho)\exp (-r_{2}u)\right \},$ (15.12)

where

$\displaystyle r_{1}=\frac{\rho+\theta(\beta_1+\beta_2)-\left [\left\{\rho+\thet... ...a_2)\right\}^{2}-4\beta_1\beta_2\theta(1+\theta)\right ]^{1/2}} {2(1+\theta)}, $

$\displaystyle r_{2}=\frac{\rho+\theta(\beta_1+\beta_2)+\left [\left\{\rho+\thet... ...a_2)\right\}^{2}-4\beta_1\beta_2\theta(1+\theta)\right ]^{1/2}} {2(1+\theta)}, $

and

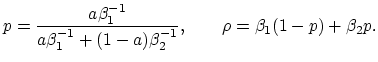
$\displaystyle p=\frac{a\beta_1^{-1}}{a\beta_1^{-1}+(1-a)\beta_2^{-1}}, \qquad \rho=\beta_1(1-p)+\beta_2 p. $

Table 15.4 shows the ruin probability values for mixture of two exponentials claims with $ \beta _1=3.5900\cdot 10^{-10}$, $ \beta _2=7.5088\cdot 10^{-9}$, $ a=0.0584$ (see Chapter 13) and the relative safety loading $ \theta=30\%$ with respect to the initial capital $ u$. As before, the ruin probability decreases as the capital grows. Moreover, the increase in the ruin probability values with respect to previous cases is dramatic. When $ u=1$ billion USD the difference between the mixture of two exponentials and exponential cases reaches $ 240\%$! As the same underlying data set was used in all cases to estimate the parameters of the distributions, it supports the thesis that a choice of the fitted distribution function and checking the goodness of fit is of paramount importance.


Table 15.4: The ruin probability for mixture of two exponentials claims with $ \beta _1=3.5900\cdot 10^{-10}$, $ \beta _2=7.5088\cdot 10^{-9}$, $ a=0.0584$ and $ \theta =0.3$ ($ u$ in USD billion).
$ u$ 0 $ 1$ $ 5$ $ 10$ $ 20$ $ 50$
             
$ \psi(u)$ 0.769231 0.587919 0.359660 0.194858 0.057197 0.001447
             

24267 STFruin04.xpl

Finally, note that it is possible to derive explicit formulae for mixture of $ n$ ($ n\geq 3$) exponentials (Wikstad; 1971; Panjer and Willmot; 1992). They are not presented here since the complexity of formulae grows as $ n$ increases and such mixtures are rather of little practical importance due to increasing number of parameters.