A stochastic process
![]() is a
model that describes the probability structure of a sequence of
observations over time. A time series
is a
model that describes the probability structure of a sequence of
observations over time. A time series ![]() is a
sample realization of a stochastic process that is observed only for a
finite number of periods, indexed by
is a
sample realization of a stochastic process that is observed only for a
finite number of periods, indexed by
![]() .
.
Any stochastic process can be partially characterized by the first
and second moments of the joint probability distribution: the set
of means,
![]() , and the set of variances and
covariances
, and the set of variances and
covariances
![]() . In order to get consistent forecast methods,
we need that the underlying probabilistic structure would be
stable over time. So a stochastic process is called weak
stationary or covariance stationary when the mean, the
variance and the covariance structure of the process is stable
over time, that is:
. In order to get consistent forecast methods,
we need that the underlying probabilistic structure would be
stable over time. So a stochastic process is called weak
stationary or covariance stationary when the mean, the
variance and the covariance structure of the process is stable
over time, that is:
Given condition (4.3), the covariance between ![]() and
and ![]() depends only on the displacement
depends only on the displacement ![]() and it is called
autocovariance at lag
and it is called
autocovariance at lag ![]() ,
, ![]() . The set of autocovariances
. The set of autocovariances
![]() ,
,
![]() , is called the
autocovariance function of a stationary process.
, is called the
autocovariance function of a stationary process.
The general Autoregressive Moving Average
model
![]() is a linear stochastic model where the variable
is a linear stochastic model where the variable ![]() is
modelled in terms of its own past values and a disturbance. It is defined
as follows:
is
modelled in terms of its own past values and a disturbance. It is defined
as follows:
where the random variable
![]() is called the innovation because it represents the part of the observed variable
is called the innovation because it represents the part of the observed variable ![]() that is unpredictable given the past values
that is unpredictable given the past values
![]() .
.
The general ![]() model (4.4) assumes that
model (4.4) assumes that ![]() is the output of a
linear filter that transforms the past innovations
is the output of a
linear filter that transforms the past innovations
![]() , that is,
, that is, ![]() is a linear process. This linearity
assumption is based on the Wold's decomposition theorem
(Wold; 1938) that says that any discrete stationary covariance process
is a linear process. This linearity
assumption is based on the Wold's decomposition theorem
(Wold; 1938) that says that any discrete stationary covariance process
![]() can be expressed as the sum of two uncorrelated processes,
can be expressed as the sum of two uncorrelated processes,
The ![]() formulation (4.4) is a finite
reparametrization of the infinite
representation (4.5)-(4.6) with
formulation (4.4) is a finite
reparametrization of the infinite
representation (4.5)-(4.6) with ![]() constant. It
is usually written in terms of the lag operator
constant. It
is usually written in terms of the lag operator ![]() defined by
defined by
![]() , that gives a shorter expression:
, that gives a shorter expression:
where the lag operator polynomials ![]() and
and
![]() are called the
are called the ![]() polynomial and the
polynomial and the ![]() polynomial,
respectively. In order to avoid parameter redundancy, we assume that
there are not common factors between the
polynomial,
respectively. In order to avoid parameter redundancy, we assume that
there are not common factors between the ![]() and the
and the ![]() components.
components.
Next, we will study the plot of some time series generated by stationary
![]() models with the aim of determining the main patterns of their
temporal evolution. Figure 4.2 includes two series generated
from the following stationary processes computed by means of the
genarma
quantlet:
models with the aim of determining the main patterns of their
temporal evolution. Figure 4.2 includes two series generated
from the following stationary processes computed by means of the
genarma
quantlet:
| Series 1: |
|
|
| *[2mm] Series 2: |
|
|
As expected, both time series move around a constant level without
changes in variance due to the stationary property. Moreover, this
level is close to the theoretical mean of the process, ![]() , and
the distance of each point to this value is very rarely outside
the bounds
, and
the distance of each point to this value is very rarely outside
the bounds
![]() . Furthermore, the evolution of the
series shows local departures from the mean of the process, which
is known as the mean reversion behavior that characterizes
the stationary time series.
. Furthermore, the evolution of the
series shows local departures from the mean of the process, which
is known as the mean reversion behavior that characterizes
the stationary time series.
Let us study with some detail the properties of the different
![]() processes, in particular, the autocovariance function which
captures the dynamic properties of a stochastic stationary
process. This function depends on the units of measure, so
the usual measure of the degree of linearity between variables is
the correlation coefficient. In the case of stationary processes,
the autocorrelation coefficient at lag
processes, in particular, the autocovariance function which
captures the dynamic properties of a stochastic stationary
process. This function depends on the units of measure, so
the usual measure of the degree of linearity between variables is
the correlation coefficient. In the case of stationary processes,
the autocorrelation coefficient at lag ![]() , denoted by
, denoted by
![]() , is defined as the correlation between
, is defined as the correlation between ![]() and
and
![]() :
:
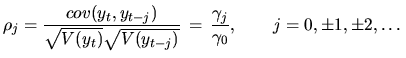
Thus, the autocorrelation function (ACF) is the autocovariance
function standarized by the variance ![]() . The properties of the ACF
are:
. The properties of the ACF
are:
Given the symmetry property (4.10), the ACF is usually represented by means of a bar graph at the nonnegative lags that is called the simple correlogram.
Another useful tool to describe the dynamics of a stationary process is
the partial autocorrelation function (PACF). The partial
autocorrelation coefficient at lag ![]() measures the linear
association between
measures the linear
association between ![]() and
and ![]() adjusted for the effects of the
intermediate values
adjusted for the effects of the
intermediate values
![]() . Therefore, it
is just the coefficient
. Therefore, it
is just the coefficient ![]() in
the linear regression model:
in
the linear regression model:
The properties of the PACF are equivalent to those of the ACF
(4.8)-(4.10) and it is easy to prove that
![]() (Box and Jenkins; 1976). Like the ACF, the partial autocorrelation
function does not depend on the units of measure and it is represented by
means of a bar graph at the nonnegative lags that is called partial
correlogram.
(Box and Jenkins; 1976). Like the ACF, the partial autocorrelation
function does not depend on the units of measure and it is represented by
means of a bar graph at the nonnegative lags that is called partial
correlogram.
The dynamic properties of each stationary model determine a particular
shape of the correlograms. Moreover, it can be shown that, for any
stationary process, both functions, ACF and PACF, approach to zero as the
lag ![]() tends to infinity. The
tends to infinity. The ![]() models are not always stationary
processes, so it is necessary first to determine the conditions for
stationarity. There are subclasses of
models are not always stationary
processes, so it is necessary first to determine the conditions for
stationarity. There are subclasses of ![]() models which have special
properties so we shall study them separately. Thus, when
models which have special
properties so we shall study them separately. Thus, when ![]() and
and
![]() , it is a white noise process, when
, it is a white noise process, when ![]() , it is a pure
moving average process of order
, it is a pure
moving average process of order ![]() ,
, ![]() , and when
, and when ![]() it is
a pure autoregressive process of order
it is
a pure autoregressive process of order ![]() ,
, ![]() .
.
The simplest ![]() model is a white noise process, where
model is a white noise process, where ![]() is a
sequence of uncorrelated zero mean variables with constant variance
is a
sequence of uncorrelated zero mean variables with constant variance
![]() . It is denoted by
. It is denoted by
![]() . This process is
stationary if its variance is finite,
. This process is
stationary if its variance is finite,
![]() , since given that:
, since given that:
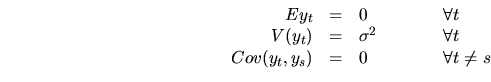
![]() verifies conditions (4.1)-(4.3).
Moreover,
verifies conditions (4.1)-(4.3).
Moreover, ![]() is uncorrelated over time, so its autocovariance function is:
is uncorrelated over time, so its autocovariance function is:
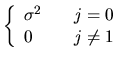 |
And its ACF and PACF are as follows:
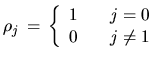 |
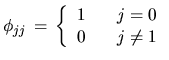 |
To understand the behavior of a white noise, we will generate a
time series of size 150 from a gaussian white noise process
![]() . Figure 4.3 shows the simulated series that
moves around a constant level randomly, without
any kind of pattern, as corresponds to the uncorrelation over time.
The economic time series will follow white noise patterns very
rarely, but this process is the key for the formulation of more
complex models. In fact, it is the starting point of the
derivation of the properties of
. Figure 4.3 shows the simulated series that
moves around a constant level randomly, without
any kind of pattern, as corresponds to the uncorrelation over time.
The economic time series will follow white noise patterns very
rarely, but this process is the key for the formulation of more
complex models. In fact, it is the starting point of the
derivation of the properties of ![]() processes given that we are
assuming that the innovation of the model is a white noise.
processes given that we are
assuming that the innovation of the model is a white noise.
The general (finite-order) moving average model of order ![]() ,
, ![]() is:
is:
It can be easily shown that ![]() processes are always stationary,
given that the parameters of any finite
processes are always stationary,
given that the parameters of any finite ![]() processes always
verify condition (4.6). Moreover, we are interested in
invertible
processes always
verify condition (4.6). Moreover, we are interested in
invertible ![]() processes. When a process is invertible, it
is possible to invert the process, that is, to express the current
value of the variable
processes. When a process is invertible, it
is possible to invert the process, that is, to express the current
value of the variable ![]() in terms of a current shock
in terms of a current shock
![]() and
its observable past values
and
its observable past values
![]() . Then,
we say that the model has an autoregressive representation.
This requirement provides a sensible way of associating present
events with past happenings. A
. Then,
we say that the model has an autoregressive representation.
This requirement provides a sensible way of associating present
events with past happenings. A ![]() model is invertible if the
model is invertible if the ![]() roots of the characteristic equation
roots of the characteristic equation
![]() lie outside
the unit circle. When the root
lie outside
the unit circle. When the root ![]() is real, this condition means
that the absolute value must be greater than unity,
is real, this condition means
that the absolute value must be greater than unity, ![]() . If
there are a pair of complex roots, they may be written as
. If
there are a pair of complex roots, they may be written as
![]() , where
, where ![]() are real numbers and
are real numbers and
![]() , and
then the invertibility condition means that its moduli must
be greater than unity,
, and
then the invertibility condition means that its moduli must
be greater than unity,
![]() .
.
Let us consider the moving average process of first order,
![]() :
:
Let us study this simple ![]() process in detail. Figure
4.4 plots simulated series of length 150 from two
process in detail. Figure
4.4 plots simulated series of length 150 from two
![]() processes where the parameters
processes where the parameters
![]() take the values
(0, 0.8) in the first model and (4, -0.5) in the second one. It can be
noted that the series show the general patterns associated with stationary
and mean reversion processes. More specifically, given that only a past
innovation
take the values
(0, 0.8) in the first model and (4, -0.5) in the second one. It can be
noted that the series show the general patterns associated with stationary
and mean reversion processes. More specifically, given that only a past
innovation
![]() affects the current value of the series
affects the current value of the series
![]() (positively for
(positively for ![]() and negatively for
and negatively for ![]() ), the
), the
![]() process is known as a very short memory process and so, there is
not a 'strong' dynamic pattern in the series. Nevertheless, it can be
observed that the time evolution is smoother for the positive value of
process is known as a very short memory process and so, there is
not a 'strong' dynamic pattern in the series. Nevertheless, it can be
observed that the time evolution is smoother for the positive value of
![]() .
.
The ACF for ![]() models is derived from the following moments:
models is derived from the following moments:
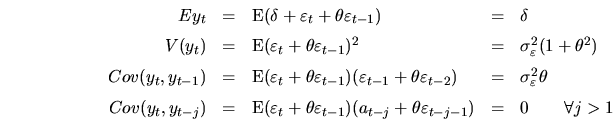
given that, for all ![]() and for all
and for all ![]() , the innovations
, the innovations
![]() are uncorrelated with
are uncorrelated with
![]() . Then, the autocorrelation function is:
. Then, the autocorrelation function is:
![$\displaystyle \left\{\begin{array}{cll}
\displaystyle\frac{\theta}{1 + \theta^2} && j = 1\\ *[2mm]
0 && j > 1
\end{array}\right.$](xegbohtmlimg1696.gif) |
That is, there is a cutoff in the ACF at the first lag. Finally, the partial autocorrelation function shows an exponential decay. Figure 4.5 shows typical profiles of this ACF jointly with the PACF.
It can be shown that the general stationary and invertible ![]() process
has the following properties (Box and Jenkins; 1976):
process
has the following properties (Box and Jenkins; 1976):
Figure 4.6 shows the simple and partial correlograms for two
different ![]() processes. Both ACF exhibit a cutoff at lag two. The
roots of the
processes. Both ACF exhibit a cutoff at lag two. The
roots of the ![]() polynomial of the first series are real, so the PACF
decays exponentially while for the second series with complex roots
the PACF decays as a damping sine-cosine wave.
polynomial of the first series are real, so the PACF
decays exponentially while for the second series with complex roots
the PACF decays as a damping sine-cosine wave.
The general (finite-order) autoregressive model of order ![]() ,
, ![]() , is:
, is:
Let us begin with the simplest ![]() process, the
autoregressive process of first order,
process, the
autoregressive process of first order, ![]() , that is defined
as:
, that is defined
as:
Figure 4.7 shows two simulated time series generated from
![]() processes with zero mean and parameters
processes with zero mean and parameters ![]() and -0.7,
respectively. The autoregressive parameter measures the persistence of past
events into the current values. For example, if
and -0.7,
respectively. The autoregressive parameter measures the persistence of past
events into the current values. For example, if ![]() , a positive (or
negative) shock
, a positive (or
negative) shock
![]() affects positively (or negatively) for a
period of time which is longer the larger the value of
affects positively (or negatively) for a
period of time which is longer the larger the value of ![]() . When
. When ![]() , the series moves more roughly around the mean due to the alternation
in the direction of the effect of
, the series moves more roughly around the mean due to the alternation
in the direction of the effect of
![]() , that is, a shock that
affects positively in moment
, that is, a shock that
affects positively in moment ![]() , has negative effects on
, has negative effects on ![]() , positive
in
, positive
in ![]() , ...
, ...
The ![]() process is always invertible and it
is stationary when the parameter of the model is constrained
to lie in the region
process is always invertible and it
is stationary when the parameter of the model is constrained
to lie in the region
![]() .
To prove the stationary condition, first we write the
.
To prove the stationary condition, first we write the ![]() in the moving average form by recursive substitution of
in the moving average form by recursive substitution of ![]() in
(4.14):
in
(4.14):
That is, ![]() is a weighted sum of past innovations. The weights
depend on the value of the parameter
is a weighted sum of past innovations. The weights
depend on the value of the parameter ![]() : when
: when ![]() , (or
, (or ![]() ), the influence of a given innovation
), the influence of a given innovation
![]() increases (or decreases)
through time. Taking expectations to (4.15) in order to compute
the mean of the process, we get:
increases (or decreases)
through time. Taking expectations to (4.15) in order to compute
the mean of the process, we get:
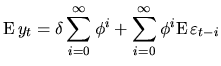
Given that
![]() , the result is a sum of infinite terms that
converges for all value of
, the result is a sum of infinite terms that
converges for all value of ![]() only if
only if ![]() , in which case
, in which case
![]() . A similar problem appears when we compute the
second moment. The proof can be simplified assuming that
. A similar problem appears when we compute the
second moment. The proof can be simplified assuming that ![]() , that
is,
, that
is, ![]() . Then, variance is:
. Then, variance is:
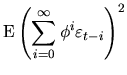 |
|||
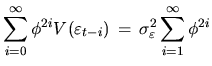 |
Again, the variance goes to infinity except for
![]() , in which
case
, in which
case
![]() . It is easy to
verify that both the mean and the variance explode when that condition
doesn't hold.
. It is easy to
verify that both the mean and the variance explode when that condition
doesn't hold.
The autocovariance function of a stationary ![]() process is
process is
Therefore, the autocorrelation function for the stationary ![]() model
is:
model
is:
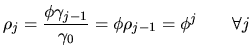
That is, the correlogram shows an exponential decay with positive values
always if ![]() is positive and with negative-positive oscillations if
is positive and with negative-positive oscillations if
![]() is negative (see figure 4.8). Furthermore, the rate of
decay decreases as
is negative (see figure 4.8). Furthermore, the rate of
decay decreases as ![]() increases, so the greater the value of
increases, so the greater the value of ![]() the stronger the dynamic correlation in the process. Finally, there
is a cutoff in the partial autocorrelation function at the first lag.
the stronger the dynamic correlation in the process. Finally, there
is a cutoff in the partial autocorrelation function at the first lag.
It can be shown that the general ![]() process
(Box and Jenkins; 1976):
process
(Box and Jenkins; 1976):
Some examples of correlograms for more complex ![]() models, such as the
models, such as the
![]() , can be seen in figure 4.9. They are very similar to
the
, can be seen in figure 4.9. They are very similar to
the ![]() patterns when the processes have real roots, but take a very
different shape when the roots are complex (see the first pair of graphics
of figure 4.9).
patterns when the processes have real roots, but take a very
different shape when the roots are complex (see the first pair of graphics
of figure 4.9).
The general (finite-order) autoregressive moving average model of orders
![]() ,
, ![]() , is:
, is:
It can be shown that the general ![]() process
(Box and Jenkins; 1976):
process
(Box and Jenkins; 1976):
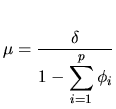
For example, the ![]() process is defined as:
process is defined as:
This model is stationary if ![]() and is invertible if
and is invertible if
![]() . The mean of the
. The mean of the ![]() stationary process can be
derived as follows:
stationary process can be
derived as follows:
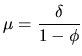 .
.
The autovariance function for an ![]() stationary process
(assuming
stationary process
(assuming ![]() ) is as follows:
) is as follows:
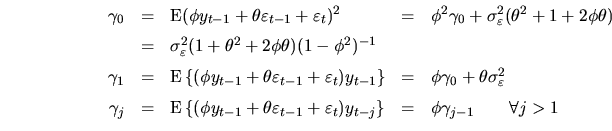
The autocorrelation function for the stationary ![]() model is:
model is:
![$\displaystyle \rho_j =
\displaystyle\left\{\begin{array}{lcr}
\phi + \displayst...
...a^2 + 2\theta \phi}
&& j=1
\\ *[2mm]
\phi \rho_{j-1} && j>1
\end{array}\right.
$](xegbohtmlimg1766.gif)