5.4 Estimation of Multiplicative SARIMA Models

This section deals with the estimation of identified SARIMA models, i.e. we want to estimate the unknown parameters $\psi$ of the multiplicative SARIMA model. If the model contains only AR terms, the unknown coefficients can be estimated using ordinary least squares. However, if the model contains MA terms too, the task becomes more complicated, because the lagged values of the innovations are unobservable. Consequently, it is not possible to derive explicit expressions to estimate the unknown coefficients and therefore one has to use maximum likelihood for estimation purposes. In the next subsection 5.4.1 the theoretical background of maximizing a likelihood function is briefly outlined.

In order to convey an idea of what follows, we will shortly outline the procedure: first, one sets up the multiplicative SARIMA model--in the following also called original model-- with some initial values for the unknown parameters $\psi$. In subsection 5.4.2 it is explained how to set the original SARIMA model using the quantlet msarimamodel. Restrictions can be imposed on the coefficients. The simplest restriction is that some of the coefficients are zero. Then the value of the likelihood function--given the initial parameters--is evaluated.

Unfortunately, in most cases the original SARIMA model cannot be estimated directly. If one looks at the SARIMA(3,1,1)$\times$(12,1,0,0) model in section 5.4.3--equation (5.18)--one recognizes on the left hand side the product of two expressions. Both of them contain lag-operators. Such expressions have to be telescoped out first. XploRe provides a very convenient tool to do so: msarimaconvert. This quantlet is explained in detail in subsection 5.4.3. The result you get from msarimaconvert is an ordinary ARMA(p,q) model which can be estimated.

Under the assumption that an ARMA model is stationary and invertible and that the observations are normally distributed, it can be estimated using the maximum likelihood approach. By making suitable assumptions about initial conditions, the maximum likelihood estimators can be obtained by minimizing the conditional sum of squares. In subsection 5.4.4 the quantlet msarimacond is presented. It calculates the conditional sum of squares function and allows for zero restrictions on the coefficients. Given this function, numerical methods have to be applied to maximize the likelihood function with respect to $\psi$.

To evaluate the fit of the estimated model, the quantlet msarimacond also delivers several criteria for diagnostic checking. The residuals of the model should be white noise. The quantlet eacf provides an easy way to check the behavior of the residuals.

However, the conditional sum of squares is not always very satisfactory for seasonal series. In that case the calculation of the exact likelihood function becomes necessary (Box and Jenkins; 1976, p. 211). One approach is to set up the likelihood function via Kalman filter techniques. We briefly discuss how to set up the airline model in state space form and how to use the Kalman filter to evaluate the exact likelihood function. Once again, numerical methods are necessary to maximize the exact likelihood function.

5.4.1 Maximum Likelihood Estimation

The approach of maximum likelihood (ML) requires the specification of a particular distribution for a sample of $T$ observations $y_t$. Let

$$f_{Y_T,Y_{T-1},\hdots,Y_1}(y_T,y_{T-1},\hdots,y_1\vert\psi)$$

denote the probability density of the sample given the unknown $(n\times1)$ parameters $\psi$. It can be interpreted as the probability of having observed the given sample (Hamilton; 1994, p. 117).

With the sample $y=\{y_T,\hdots,y_1\}$ at hand, the above given probability can be rewritten as a function of the unknown parameters given the sample $y$. Following the notation of Box and Jenkins (1976), we use the notation $L(\psi\vert y)$. In most cases it is easier to work with the log likelihood function $l(\psi\vert y)=\ln{L(\psi\vert y)}$.

The maximum likelihood estimate $\tilde{\psi}$ is the parameter vector that maximizes the probability for the observed sample $y$. Thus, the MLE satisfies the so-called likelihood equations, which are obtained by differentiating $l(\psi\vert y)$ with respect to each of the unknown parameters of the vector $\psi$ and setting the derivatives to zero (Harvey; 1993). Using vector notation and suppressing $y$, we obtain

$$\frac{\partial l(\psi)}{\partial{\psi}}=0.$$ (5.8)

As a rule, the likelihood equations are non-linear. Therefore, the ML estimates must be found in the course of an iterative procedure. This is true for the exact likelihood function of every Gaussian ARMA(p,q) process (see Hamilton; 1994, Chapter 5).

As already mentioned above, there are two different likelihood functions in use: the conditional and the exact likelihood function. Both alternatives can be estimated using XploRe.

In many applications of ARMA models the conditional likelihood function is an alternative to the exact likelihood function. In that case, one assumes that the first $p$ observations of a Gaussian ARMA(p,q) process are deterministic and are equal to its observed values $\{y_p,\hdots,y_1\}$. The initial residuals $a_t$ for $t\in\{p,\hdots,p-q+1\}$ are set to its expected values 0. The log likelihood function for this setting is of the following form with $\psi=(\psi',\sigma^2)$

$$l(\psi)= -\frac{1}{2}(T-p)\ln{2}\pi-\frac{1}{2}(T-p) \ln{\sigma^2}-\frac{S(\psi')}{2\sigma^2}$$ (5.9)

and $S(\psi')$ denoting the sum of squares function

$$S(\psi')=\sum_{t=p+1}^{T}\left(a_t(\psi')\right)^2.$$ (5.10)

The notation $a_t(\psi')$ emphasizes that $a_t$ is no longer a disturbance, but a residual which depends on the value taken by the variables in $\psi'$.

Note, that the parameter $\sigma ^2$ is an additional one, that is not included in vector $\psi'$. It is easy to see that (5.9) is maximized with respect to $\psi'$ if the sum of squares $S(\psi')$ is minimized. Using the condition (5.8), this leads to

$$\sum_{t=1}^{T}\frac{\partial a_t(\psi')}{\partial \psi'} \ a_t=0.$$ (5.11)

Thus, the ML estimate for $\psi'$ can be obtained by minimizing (5.10). Furthermore, we obtain from (5.9) and (5.8) that

$$\tilde{\sigma}^2=\frac{S(\tilde{\psi}')}{T-p}\;.$$ (5.12)

Thus, given the parameter vector $\tilde{\psi}'$ that maximizes the sum of squares--and thus the conditional log likelihood function (5.9)--one divides the sum of squares by $T-p$ to obtain the ML estimate $\tilde{\sigma}^2$. Another estimator for the variance of the innovations corrects furthermore for the number of estimated coefficients $k$.

As already mentioned, one approach to calculate the exact log likelihood is to use the Kalman filter. We want to show this for the airline model. This model is rewritable in state space form (SSF) as

where $I_{13}$ is a $(13\times13)$ identity matrix (Koopman, Shephard and Doornik; 1999). Here,

$$\begin{bmatrix}0 & I_{13} \\ 0 & 0 \\ \end{bmatrix}$$ (5.14)

is the so-called transition matrix.

Given Gaussian error terms $a_t$, the value of the log likelihood function $l(\psi)$ for the above given state space form is

$$-\frac{T}{2}\ln{2\pi}-\frac{1}{2}\sum_{t=1}^T\ln{\vert F_t\vert}-\frac{1}{2}\sum_{t=1}^T v_t^\top F_t^{-1}v_t\;.$$ (5.15)

Here,

$$v_t\equiv y_t-Z_t [\alpha_t\vert\mathcal{F}_{t-1}]$$

are the innovations of the Kalman filtering procedure and $\mathcal{F}_{t-1}$ is the information set up to $t-1$. $Z_t$ is the matrix from the above given state space form that contains the identity matrix. The matrix $F_t$ is the covariance matrix of the innovations in period $t$ and it is a by-product of the Kalman filter. The above log likelihood is known as the prediction error decomposition form (Harvey; 1989).

Given some initial values for $\psi$, the above exact log likelihood is evaluated with the Kalman filter. Using numerical methods, the function is maximized with respect to $\psi$.

Once the ML estimate $\tilde{\psi}$ is calculated, one wants to have standard errors for testing purposes. If $T$ is sufficiently large, the ML estimate $\tilde{\psi}$ is approximately normally distributed with the inverse of the information matrix divided by $T$ as covariance matrix. The inverse of the Hessian for $l(\tilde{\psi})$ is one way to estimate the covariance matrix (Hamilton; 1994, Section 5.8). One can calculate the Hessian applying numerical methods.

5.4.2 Setting the Multiplicative SARIMA Model

msarimamodelOut = msarimamodel (d,arma,season)

sets the coefficients of a multiplicative seasonal ARIMA model

The original model is specified by means of the quantlet msarimamodel . The three arguments are lists that give the difference orders $(d,D)$, the ordinary ARMA parts $\Phi(L)$ and $\Theta(L)$, and the seasonal AR and MA polynomials $\Phi_s(L)$ and $\Theta_s(L)$. If the model has no seasonal difference, one just omits $D$.

The arma list has at most four elements: the first element is a vector that specifies the lags of the AR polynomial $\Phi(L)$ that are not zero. The second element is a vector that specifies the lags of the MA polynomial $\Theta(L)$. If the model has only one polynomial, one sets the lags of the other one to 0.

The third element of the arma list is a vector with

-

the AR coefficients

i)

if the model has both an AR and a MA polynomial

ii)

if the model has only an AR polynomial

-

the MA coefficients if the model has only a MA polynomial.

If the model has both an AR and a MA polynomial then the fourth argument is necessary. It is a list that contains the coefficients of the MA polynomial. For example,

arma = list((1|3),0,(0.1|-0.25))

specifies an ARMA(3,0) part with $\phi_2=0$, $\phi_1=0.1$ and $\phi_3=-0.25$.

The last argument season is a list that contains the information concerning the seasonal AR and MA polynomials. This list has at most five elements: the first element specifies the season $s$. If the data show no seasonal pattern, one sets $s=0$ as the only argument of the list season. The second element is the lag structure of the seasonal AR polynomial. You have to fill in the lags that are different from zero. The third element is the lag structure of the seasonal MA polynomial. The last two elements are for the coefficient vectors of the polynomials. As explained for the arma list, one can omit the respective vector if the model has only one polynomial. For example,

season = list(12,0,(1|4),(-0.3|0.1))

gives a model with no seasonal AR polynomial and with the seasonal MA(4) polynomial

$$1-0.3L^{12}+0.1L^{48}\;.$$ (5.16)

To understand what msarimamodel does, let us assume that the multiplicative SARIMA model is given as

$$(1-0.1L+0.25L^3)\Delta x_t=(1-0.3L^{12}+0.1L^{48})\varepsilon_t\;.$$ (5.17)

Here $d=1$ and $D=0$, so that we can set d=1. The lists for the ordinary and seasonal polynomials are given above. To have a look at the output of msarimamodel, one just compiles the following piece of XploRe code

arma   = list((1|3),0,(0.1|-0.25))   ; ordinary ARMA part
season = list(12,0,(1|4),(-0.3|0.1)) ; seasonal ARMA part
msarimamodelOut = msarimamodel(1,arma,season)
msarimamodelOut ; shows the elements of msarimamodelOut

The output is

Contents of msarimamodelOut.d
[1,]        1
Contents of msarimamodelOut.arlag
[1,]        1
[2,]        3
Contents of msarimamodelOut.malag
[1,]        0
Contents of msarimamodelOut.s
[1,]       12
Contents of msarimamodelOut.sarlag
[1,]        0
Contents of msarimamodelOut.smalag
[1,]        1
[2,]        4
Contents of msarimamodelOut.phi
[1,]      0.1
[2,]    -0.25
Contents of msarimamodelOut.theta
[1,]        0
Contents of msarimamodelOut.Phi
[1,]        0
Contents of msarimamodelOut.Theta
[1,]     -0.3
[2,]      0.1

and it resembles our example in general notation (see equation (5.4)). The list msarimamodelOut is an easy way to check the correct specification of the model.

5.4.3 Setting the Expanded Model

{y,phiconv,thetaconv,k} = msarimaconvert (x,msarimamodelOut)

sets the coefficients of an expanded multiplicative seasonal ARIMA model

If you want to estimate the coefficients in (5.4), you have to telescope out the original model. Given the specification by the list msarimaOut (see Subsection 5.4.2) and the time series $\{x_t\}_{t=1}^T$, the quantlet msarimaconvert telescopes out the original model automatically.

Let us consider the following SARIMA(3,1,1)$\times$(12,1,0,0) model with $\phi_2=0$:

$$(1-\phi_{s,1}L^{12})(1-\phi_1 L-\phi_3L^{3})\Delta{x_t}=(1+\theta_1L)a_t.$$ (5.18)

Telescoping out the polynomials on the left-hand side leads to an ordinary ARMA model:

$$(1-\phi^e_1L-\phi^e_3L^3-\phi^e_{12}L^{12}-\phi^e_{13}L^{13}-\phi^e_{15}L^{15})y_t=(1+\theta^e_1L)a_t$$ (5.19)

with $y_t\stackrel{\mathrm{def}}{=}\Delta x_t$, $\phi^e_1\stackrel{\mathrm{def}}{=}\phi_1$, $\phi^e_3\stackrel{\mathrm{def}}{=}\phi_3$, $\phi^e_{12}\stackrel{\mathrm{def}}{=}\phi_{s,1}$, $\phi^e_{13}\stackrel{\mathrm{def}}{=}-\phi_1\phi_{s,1}$, $\phi^e_{15}\stackrel{\mathrm{def}}{=}-\phi_3\phi_{s,1}$, and $\theta^e_1\stackrel{\mathrm{def}}{=}\theta_1$.

The superscript $e$ denotes the coefficients of the expanded model. The output of the quantlet is thus self-explaining: the series $y_t$ is just the differenced original series $x_t$ and the other two outputs are the vector $\phi^e$ (with $\phi^e_0\stackrel{\mathrm{def}}{=}1$) and the vector $\theta^e$ (with $\theta^e_0\stackrel{\mathrm{def}}{=}1$). The first vector has the dimension $(sP+p+1)\times1$ and second one has the dimension $(sQ+q+1)\times1$. The scalar $k$ gives the number of coefficients in the original model. For the above given example, we have $k=4$, whereas the number of coefficients of the expanded model is 6. Later on, we need $k$ for the calculation of some regression diagnostics.

5.4.4 The Conditional Sum of Squares

{S,dia} = msarimacond (y,phiconv,thetaconv,mu{,k})

calculates the conditional sum of squares for given vectors of coefficients

The sum of squares is a criterion that can be used to identify the coefficients of the best model. The output of the quantlet is the conditional sum of squares for a given model specification (Box and Jenkins; 1976, Chapter 7).

For an ARMA(p,q) model this sum is just

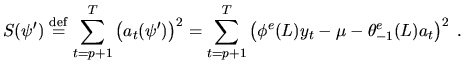$$S(\psi')\stackrel{\mathrm{def}}{=}\sum_{t=p+1}^T\left(a_t(\psi')\right)^2= \sum_{t=p+1}^T\left(\phi^e(L)y_t-\mu-\theta^e_{-1}(L)a_t\right)^2\;.$$ (5.20)

Here $T$ denotes the number of observations $y_t$. Recall that the first entries of the lag-polynomials are for $L^0=1$. $\theta^e_{-1}(L)$ denotes the MA-polynomial without the first entry. The first $q$ residuals are set to zero.

The arguments of the quantlet are given by the output of msarimaconvert . mu is the mean of the series $\{y_t\}_{t=1}^T$. $k$ is the number of coefficients in the original model and will be used to calculate some regression diagnostics. This argument is optional. If you do not specify $k$, the number of coefficients in the expanded model is used instead.

Furthermore, the quantlet msarimacond gives the list dia that contains several diagnostics. After the maximization of the conditional sum of squares, one can use these diagnostics to compare different specifications. In the ongoing $k$ denotes the number of ARMA parameters that are different from zero. In our example we have $k=2$ for both specifications.

The first element of the list--that is dia.s2--is the estimated variance of the residuals

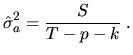$$\hat{\sigma}^2_a=\frac{S}{T-p-k}\;.$$ (5.21)

The second element dia.R2 gives the coefficient of determination

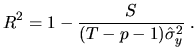$$R^2=1-\frac{S}{(T-p-1)\hat{\sigma}^2_y}\;.$$ (5.22)

The variance of the dependent variables $y_t$ is calculated for the observations starting with $t=p+1$. It is possible in our context that $R^2$ becomes negative.

The adjusted coefficient of determination $\bar{R}^2$ is calculated as

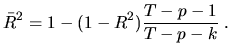$$\bar{R}^2 = 1-(1-R^2)\frac{T-p-1}{T-p-k}\;.$$ (5.23)

It is the third argument of the list and is labeled dia.aR2.

The fourth element dia.logl gives the values of the log likelihood function evaluated at $\tilde{\psi}$. Given the likelihood function (5.9), $\tilde{\sigma}^2$ is a function of $\tilde{\psi}'$. To take this into account, we plug (5.12) into (5.9) and obtain

$$l(\tilde{\psi})=-\frac{T-p}{2}\left[1+\ln{2\pi}+\ln{\left\{\frac{S(\tilde{\psi}')}{T-p}\right\}}\right]\;.$$ (5.24)

This expression is the value of the log likelihood function.

The fifth element dia.AIC gives the Akaike Information Criteria (AIC)

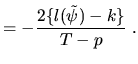$$= -\frac{2\{l(\tilde{\psi})-k\}}{T-p}\;.$$ (5.25)

The sixth element dia.SIC gives the Schwarz Information Criteria (SIC)

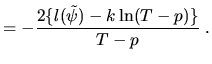$$= -\frac{2\{l(\tilde{\psi})-k\ln(T-p)\}}{T-p}\;.$$ (5.26)

For both criteria see Shumway and Stoffer (2000). These criteria can be used for model selection (Durbin and Koopman (2001)). Eventually, the last element dia.a gives the $(T-p)\times1$ vector of the residuals $a_t$.

Now we can come back to our example of the airline data: recall that we have identified two possible specifications for this data set. The first specification is a SARIMA(0,1,1)$\times$(12,0,1,1) with $\psi_1=(\theta_1,\theta_{s,1},\sigma^2)$. The second is a SARIMA(0,1,12)$\times$(12,0,1,0) with $\psi_2=(\theta_1,\theta_{12},\sigma^2)$.

We maximize the conditional sum of squares for both specifications using the BFGS algorithm. Given the estimates $\tilde{\psi}$, the standard errors are obtained by means of the Hessian matrix for the log likelihood. The Hessian is calculated for this function using numerical methods. The square roots of the diagonal elements of the inverse Hessian are the standard errors of the estimates $\tilde{\psi}'$.

The results of the first specification are obtained using the the quantlet

XEGmsarima9.xpl

and the results of the second specification can be also obtained with the quantlet

XEGmsarima10.xpl

It is obvious that both specifications deliver good results. However, the sum of squared resids is smaller for the specification with a seasonal MA term. Additionally, both information criteria indicate that this specification is slightly better.

5.4.5 The Extended ACF

eacf (y,p,q)

displays a table with the extended ACF for time series $y_t$

After estimating the unknown parameters $\tilde{\psi}$ for competing specifications, one should have a look at the residual series $\{\tilde{a}_t\}_{t=p+1}^T$. They should behave like a white noise process and should exhibit no autocorrelation. In order to check for autocorrelation, one could use the ACF and PACF. However, the extended autocorrelation function (EACF) is also a convenient tool for inspecting time series (Peña, Tiao and Tsay; 2001, Chapter 3) that show no seasonal pattern.

In general, the EACF allows for the identification of ARIMA models (differencing is not necessary). The quantlet eacf generates a table of the sample EACF for a time series. You have to specify the maximal number of AR lags (p) and MA lags (q). Every row of the output table gives the ACF up to q lags for the residuals of an AR regression with $k\leqslant p$ lags. Furthermore, the simplified EACF is tabulated. If an autocorrelation is significant according to Bartlett's formula the entry is 1. Otherwise the entry is 0. Bartlett's formula for an MA(q) is given as

$$\textrm{Var}[\hat{\rho}(q+1)]=\frac{1}{T}\left[1+2\sum_{j=1}^q\hat{\rho}(j)^2\right]$$

where $T$ is the number of observations (Peña, Tiao and Tsay; 2001). For identification, look for the vertex of a triangle of zeros. You can immediately read off the order of the series from the table.

We use the EACF to explore the behavior of the residuals of both specifications. The next quantlet computes the EACF of the residuals that come from the SARIMA(0,1,1) $\times$(12,0,1,1) specification.

XEGmsarima11.xpl

It is obvious, that the vertex of zeros is at position $q=0$ and $p= 0$. Thus we conclude that the residuals are white noise. Notice, that the first line in the above table at $p= 0$ just gives the ACF of the residual series. According to Bartlett's formula, all autocorrelation coefficients are not significantly different from zero.

The next quantlet computes the EACF of the residuals of the SARIMA(0,1,12)$\times$ (12,0,1,0) specification.

XEGmsarima12.xpl

We can conclude that the vertex of zeros is at position $q=0$ and $p= 0$. Thus the residuals are white noise. According to Bartlett's formula, once again all autocorrelation coefficients are not significantly different from zero.

5.4.6 The Exact Likelihood

{gkalfilOut,loglike} = gkalfilter (Y,mu,Sig,ca,Ta,Ra, da,Za,Ha,l)

Kalman filters a SSF and gives the value of the log likelihood

As already mentioned in the introductory part of this section, the Kalman filter can be used to evaluate the exact log likelihood function. For the estimation of the unknown parameters the evaluated log likelihood function 5.15 is required. The second element of the quantlet provides the value of the exact log likelihood function.

We now shortly describe the procedure of the Kalman filter and the implementation with gkalfilter . Good references for the Kalman filter are--in addition to Harvey (1989)--Hamilton (1994), Gourieroux and Monfort (1997) and Shumway and Stoffer (2000). The first argument is an array with the observed time series. The vector mu specifies the initial conditions of the filtering procedure with corresponding covariance matrix Sig. Due to the fact that our SSF (5.13) contains no constants, we set ca and da to zero. Furthermore, we have no disturbance in the measurement equation--that is the equation for $y_t$ in (5.13)--so we also set Ha to zero. The covariance matrix for the disturbance in the state equation is given as

$$R = \sigma^2\begin{bmatrix}1 & \theta_1 & 0 & \hdots & 0 & \theta... ... \hdots & 0 & \theta_1\theta_{s,1}^2 & \theta_1^2\theta_{s,1}^2\\ \end{bmatrix}$$

Eventually, Za is an array for the matrix $Z$ given in the measurement equation.

The state space form of the airline model is given in (5.13). It is a well known fact that the product of eigenvalues for a square matrix is equal to its determinant. The determinant of the transition matrix $T$ for our model--given in equation (5.14)--is zero and so all eigenvalues are also zero. Thus our system is stable (Harvey; 1989, p. 114). In that case, we should set the initial values to the unconditional mean and variance of the state vector (Koopman, Shephard and Doornik; 1999). We easily obtain for our model (5.13) that

$$\mu \stackrel{\mathrm{def}}{=}\textrm{E}[\alpha_0]=0$$ (5.27)

and

$$\Sigma \stackrel{\mathrm{def}}{=}\textrm{Var}[\alpha_0] = T\Sigma T^\top +R\;.$$

A way to solve for the elements of $\Sigma$ is

$$(\Sigma) = (I-T\otimes T)^{-1} (R)\;.$$ (5.28)

Here, vec denotes the vec-operator that places the columns of a matrix below each other and $\otimes$ denotes the Kronecker product.

For the estimation, we use the demeaned series of the growth rates $g_t$ of the airline data. The standard errors of the estimates are given by the square roots of the diagonal elements of the inverse Hessian evaluated at $\tilde{\psi}'$. The following table shows the results:

 "==================================================================="
 " Estimation results for the SARIMA(0,1,12)x(12,0,1,0) specification"
 " Exact Log Likelihood function is maximized                        "
 "==================================================================="
 " Convergence achieved after 12 iterations                          "
 " 131 observations included                                         "
 "                                                                   "
 "      Variable       Coefficient        t-stat      p-value        "
 "      ------------------------------------------------------       "
 "      theta_1          -0.3998         -4.4726        0.00         "
 "      theta_12         -0.5545         -7.5763        0.00         "
 "      sigma2            0.0014          8.0632        0.00         "
 "      ------------------------------------------------------       "
 "      AIC              -3.6886          SIC          -3.5111       "
 "==================================================================="

XEGmsarima13.xpl

The estimators are only slightly different from the estimators we have calculated with the conditional likelihood. The variance $\tilde{\sigma}^2$ is identical.