10.1 Introduction

Volatility clustering, i.e. positive correlation of price variations observed on speculative markets, motivated the introduction of autoregressive conditionally heteroskedastic (ARCH) processes by Engle (1982) and its popular generalizations by Bollerslev (1986) (Generalized ARCH, GARCH) and Nelson (1991) (exponential GARCH, EGARCH). Being univariate in nature, however, such models neglect a further stylized fact of empirical price variations, namely contemporaneous cross correlation e.g. over a set of assets, stock market indices, or exchange rates.

Cross section relationships are often implied by economic theory. Interest rate parities, for instance, provide a close relation between domestic and foreign bond rates. Assuming absence of arbitrage, the so-called triangular equation formalizes the equality of an exchange rate between two currencies on the one hand and an implied rate constructed via exchange rates measured towards a third currency. Furthermore, stock prices of firms acting on the same market often show similar patterns in the sequel of news that are important for the entire market (Hafner and Herwartz; 1998). Similarly, analyzing global volatility transmission Engle, Ito and Lin (1990) and Hamao, Masulis and Ng (1990) found evidence in favor of volatility spillovers between the world's major trading areas occurring in the sequel of floor trading hours. From this point of view, when modeling time varying volatilities, a multivariate model appears to be a natural framework to take cross sectional information into account. Moreover, the covariance between financial assets is of essential importance in finance. Effectively, many problems in financial practice like portfolio optimization, hedging strategies, or Value-at-Risk evaluation require multivariate volatility measures (Cecchetti, Cumby and Figlewski; 1988; Bollerslev et al.; 1988).

10.1.1 Model specifications

Let $\varepsilon _t=(\varepsilon _{1t},\varepsilon _{2t},\ldots,\varepsilon _{Nt})^\top$ denote an $N$-dimensional error process, which is either directly observed or estimated from a multivariate regression model. The process $\varepsilon _t$ follows a multivariate GARCH process if it has the representation

$$\varepsilon _t = \Sigma^{1/2}_t \xi_t,$$ (10.1)

where $\Sigma_t$ is measurable with respect to information generated up to time $t-1$, denoted by the filtration $\mathcal{F}_{t-1}$. By assumption the $N$ components of $\xi_t$ follow a multivariate Gaussian distribution with mean zero and covariance matrix equal to the identity matrix.

The conditional covariance matrix, $\Sigma_t=\textrm{E}[\varepsilon _t \varepsilon _t^\top \vert\mathcal{F}_{t-1}]$, has typical elements $\sigma_{ij}$ with $\sigma_{ii},i=1,\ldots,N,$ denoting conditional variances and off-diagonal elements $\sigma_{ij},i,j=1,\ldots,N,\,i \ne j$, denoting conditional covariances. To make the specification in (10.1) feasible a parametric description relating $\Sigma_t$ to $\mathcal{F}_{t-1}$ is necessary. In a multivariate setting, however, dependencies of the second order moments in $\Sigma_t$ on $\mathcal{F}_{t-1}$ become easily computationally intractable for practical purposes.

Let vech($A$) denote the half-vectorization operator stacking the elements of a quadratic ( $N \times N)$-matrix $A$ from the main diagonal downwards in a $\frac{1}{2}N(N+1)$ dimensional column vector. Within the so-called vec-representation of the GARCH($p,q$) model $\Sigma_t$ is specified as follows:

$$\textrm{vech}(\Sigma_t) = c + \sum_{i=1}^q \tilde{A}_i \textrm{ve... ...arepsilon _{t-i}^\top ) + \sum_{i=1}^p \tilde{G}_i \textrm{vech}(\Sigma_{t-i}).$$ (10.2)

In (10.2) the matrices $\tilde{A}_i$ and $\tilde{G}_i$ each contain $\{N(N+1)/2\}^2$ elements. Deterministic covariance components are collected in $c$, a column vector of dimension $N(N+1)/2$. We consider in the following the case $p=q=1$ since in applied work the GARCH(1,1) model has turned out to be particularly useful to describe a wide variety of financial market data (Bollerslev, Engle and Nelson, 1994).

On the one hand the vec-model in (10.2) allows for a very general dynamic structure of the multivariate volatility process. On the other hand this specification suffers from high dimensionality of the relevant parameter space, which makes it almost intractable for empirical work. In addition, it might be cumbersome in applied work to restrict the admissible parameter space such that the implied matrices $\Sigma_t,\, t=1,\ldots,T$, are positive definite. These issues motivated a considerable variety of competing multivariate GARCH specifications.

Prominent proposals reducing the dimensionality of (10.2) are the constant correlation model (Bollerslev; 1990) and the diagonal model (Bollerslev et al.; 1988). Specifying diagonal elements of $\Sigma_t$ both of these approaches assume the absence of cross equation dynamics, i.e. the only dynamics are

$$\sigma_{ii,t} = c_{ii} + a_{i} \varepsilon _{i,t-1}^2 + g_{i} \sigma_{ii,t-1}, \; i=1,\ldots,N.$$ (10.3)

To determine off-diagonal elements of $\Sigma_t$ Bollerslev (1990) proposes a constant contemporaneous correlation,

$$\sigma_{ij,t} = \rho_{ij} \sqrt{\sigma_{ii} \sigma_{jj}}, \, i,j=1,\ldots,N,$$ (10.4)

whereas Bollerslev et al. (1988) introduce an ARMA-type dynamic structure as in (10.3) for $\sigma_{ij,t}$ as well, i.e.

$$\sigma_{ij,t} = c_{ij} + a_{ij} \varepsilon _{i,t-1} \varepsilon _{j,t-1} + g_{ij} \sigma_{ij,t-1}, \, i,j=1,\ldots,N.$$ (10.5)

For the bivariate case ($N=2$) with $p=q=1$ the constant correlation model contains only 7 parameters compared to 21 parameters encountered in the full model (10.2). The diagonal model is specified with 9 parameters. The price that both models pay for parsimonity is in ruling out cross equation dynamics as allowed in the general vec-model. Positive definiteness of $\Sigma_t$ is easily guaranteed for the constant correlation model ( $\vert\rho_{ij}\vert<1$), whereas the diagonal model requires more complicated restrictions to provide positive definite covariance matrices.

The so-called BEKK-model (named after Baba, Engle, Kraft and Kroner, 1990) provides a richer dynamic structure compared to both restricted processes mentioned before. Defining $N \times N$ matrices $A_{ik}$ and $G_{ik}$ and an upper triangular matrix $C_0$ the BEKK-model reads in a general version as follows:

$$\Sigma_t = C_0^\top C_0 + \sum_{k=1}^K \sum_{i=1}^q A_{ik}^\top \... ..._{t-i}^\top A_{ik} + \sum_{k=1}^K \sum_{i=1}^p G_{ik}^\top \Sigma_{t-i} G_{ik}.$$ (10.6)

If $K=q=p=1$ and $N=2$, the model in (10.6) contains 11 parameters and implies the following dynamic model for typical elements of $\Sigma_t$:

$$\sigma_{11,t} = c_{11} + a_{11}^2 \varepsilon _{1,t-1}^2 + 2 a_{11} a_{21} \varepsilon _{1,t-1} \varepsilon _{2,t-1} + a_{21}^2 \varepsilon _{2,t-1}^2$$

$$+ g_{11}^2 \sigma_{11,t-1} + 2 g_{11} g_{21} \sigma_{21,t-1} + g_{21}^2 \sigma_{22,t-1},$$

$$\sigma_{21,t} = c_{21} + a_{11} a_{22} \varepsilon _{1,t-1}^2 + (a_{21} a_{12} + ... ...varepsilon _{1,t-1} \varepsilon _{2,t-1} + a_{21} a_{22} \varepsilon _{2,t-1}^2$$

$$+ g_{11} g_{22} \sigma_{11,t-1} + (g_{21}g_{12} + g_{11}g_{22}) \sigma_{12,t-1} + g_{21} g_{22} \sigma_{22,t-1},$$

$$\sigma_{22,t} = c_{22} + a_{12}^2 \varepsilon _{1,t-1}^2 + 2 a_{12} a_{22} \varepsilon _{1,t-1} \varepsilon _{2,t-1} + a_{22}^2 \varepsilon _{2,t-1}^2$$

$$+ g_{12}^2 \sigma_{11,t-1} + 2 g_{12} g_{22} \sigma_{21,t-1} + g_{22}^2 \sigma_{22,t-1}.$$

Compared to the diagonal model the BEKK-specification economizes on the number of parameters by restricting the vec-model within and across equations. Since $A_{ik}$ and $G_{ik}$ are not required to be diagonal, the BEKK-model is convenient to allow for cross dynamics of conditional covariances. The parameter $K$ governs to which extent the general representation in (10.2) can be approximated by a BEKK-type model. In the following we assume $K=1$. Note that in the bivariate case with $K=p=q=1$ the BEKK-model contains 11 parameters. If $K=1$ the matrices $A_{11}$ and $-A_{11}$, imply the same conditional covariances. Thus, for uniqueness of the BEKK-representation $a_{11}>0$ and $g_{11}>0$ is assumed. Note that the right hand side of (10.6) involves only quadratic terms and, hence, given convenient initial conditions, $\Sigma_t$ is positive definite under the weak (sufficient) condition that at least one of the matrices $C_0$ or $G_{ik}$ has full rank (Engle and Kroner; 1995).

10.1.2 Estimation of the BEKK-model

As in the univariate case the parameters of a multivariate GARCH model are estimated by maximum likelihood (ML) optimizing numerically the Gaussian log-likelihood function.

With $f$ denoting the multivariate normal density, the contribution of a single observation, $l_t,$ to the log-likelihood of a sample is given as:

$$l_t = \ln\{f(\varepsilon _t\vert\mathcal{F}_{t-1})\}$$

$$= -\frac{N}{2}\ln(2\pi) - \frac{1}{2} \ln(\vert\Sigma_t\vert) - \frac{1}{2} \varepsilon _t^\top \Sigma^{-1}_t \varepsilon _t.$$

Maximizing the log-likelihood, $l = \sum_{t=1}^T l_t$, requires nonlinear maximization methods. Involving only first order derivatives the algorithm introduced by Berndt et al. (1974) is easily implemented and particularly useful for the estimation of multivariate GARCH processes.

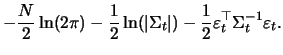If the actual error distribution differs from the multivariate normal, maximizing the Gaussian log-likelihood has become popular as Quasi ML (QML) estimation. In the multivariate framework, results for the asymptotic properties of the (Q)ML-estimator have been derived recently. Jeantheau (1998) proves the QML-estimator to be consistent under the main assumption that the considered multivariate process is strictly stationary and ergodic. Further assuming finiteness of moments of $\varepsilon _t$ up to order eight, Comte and Lieberman (2000) derive asymptotic normality of the QML-estimator. The asymptotic distribution of the rescaled QML-estimator is analogous to the univariate case and discussed in Bollerslev and Wooldridge (1992).