|
The title of this section is taken from Maddala's (1983) well-known book of the same name which is still a very good reference for parametric models of this kind. XploRe 's metrics library covers some of the parametric models. Its comparative strength, however, is in the semiparametric models for data with limited-dependent and qualitative dependent variables, which have been developed more recently. We will first discuss the parametric models and then turn to their semiparametric competitors.
|
Probit, Logit and Tobit are among the three most widely used parametric models for analyzing data with limited-dependent or qualitative dependent variables. Probit and Logit can be viewed as special cases of the generalized linear model (GLM). This is the perspective taken in XploRe . Hence we ask you to consult GLM (7) for a description of XploRe 's Probit and Logit (standard Logit, conditional Logit, multinomial Logit) quantlets.
The Tobit model is a parametric censored regression model. Formally, the model is given by
It is well known that an OLS regression of the nonzero ![]() s on the
explanatory variables
s on the
explanatory variables ![]() will not produce consistent estimates of
the regression coefficients in this situation. The model implies
the following conditional mean function :
will not produce consistent estimates of
the regression coefficients in this situation. The model implies
the following conditional mean function :
XploRe
offers a two-step estimation of ![]() In the first step, a
pilot estimate of
In the first step, a
pilot estimate of
![]() is obtained by estimating
the model
is obtained by estimating
the model
![]() by Probit analysis (here,
by Probit analysis (here,
![]() denotes the indicator function). Using this pilot estimate
denotes the indicator function). Using this pilot estimate
![]() , we can compute
, we can compute
![]() and
and
![]() and use them as regressors when we
estimate (12.2) on the part of the sample where
and use them as regressors when we
estimate (12.2) on the part of the sample where ![]()
The tobit quantlet takes the observed x and y as inputs and returns the vector of estimated coefficients b, the estimated standard deviation of the error term s and the estimated covariance matrix cv of b and s:
{b, s, cv} = tobit(x, y)
The dependent variable must be equal to 0 for the censored
observations. The known constant ![]() in (12.1) is subsumed in the
constant term of
in (12.1) is subsumed in the
constant term of ![]() That is, the estimated constant term is an estimate
of the original constant term minus
That is, the estimated constant term is an estimate
of the original constant term minus ![]()
In the following example, simulated data is used to illustrate the
use of
 tobit
:
tobit
:
library("metrics")
randomize(241200)
n = 500
k = 2
x = matrix(n)~aseq(1, n ,0.25)
s = 8
u = s*normal(n)
b = #(-9, 1)
ystar = x*b+u
y = ystar.*(ystar.>=0)
tstep = tobit(x,y)
dg = matrix(rows(tstep.cv),1)
dig = diag(dg)
stm = dig.*tstep.cv
std = sqrt(sum(stm,2))
coef = tstep.b|tstep.s
coef~(coef./std) ; t-ratios
Contents of _tmp [1,] -9.7023 -11.201 [2,] 1.0092 92.13 [3,] 6.8732 4.5859
XploRe
offers several quantlets to estimate semiparametric regression
models where the conditional mean of ![]() is assumed to depend on
the explanatory variables
is assumed to depend on
the explanatory variables ![]() only via a function of the single (linear) index
only via a function of the single (linear) index
![]() :
:
Define the vector of average derivatives of ![]() with respect to
with respect to ![]() as
as
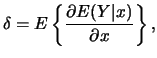 |
(12.4) |
 adeind
,
adeind
,
 dwade
and
dwade
and
 adeslp
which return estimates of the average derivative
adeslp
which return estimates of the average derivative Two comments are in order:
 adedis
which estimates the coefficients of discrete components of
adedis
which estimates the coefficients of discrete components of  adeind
,
adeind
,
 dwade
and
dwade
and
 adeslp
to estimate the average derivative in any regression
model where it exists. See Stoker (1991) and
Härdle and Stoker (1989) for discussions of the interpretation of
the average derivative in regression models that are not of the
single index form.
adeslp
to estimate the average derivative in any regression
model where it exists. See Stoker (1991) and
Härdle and Stoker (1989) for discussions of the interpretation of
the average derivative in regression models that are not of the
single index form.
Here is an overview of the
XploRe
commands for estimating the vector
of average derivatives ![]() (and thereby
(and thereby ![]() up to scale in a SIM):
up to scale in a SIM):
|
We will cover all quantlets, except for
 adeslp
, which is
discussed in Stoker (1991).
adeslp
, which is
discussed in Stoker (1991).
It can be shown that
Equation (12.7) defines the average derivative
estimator (ADE) of Härdle and Stoker (1989) which is computed
by the
XploRe
quantlet
 adeind
:
adeind
:
{delta, dvar} = adeind(x, y, d, h)
 adeind
takes the data (x and y) as well as the bandwidth
h and the binwidth d as inputs.
adeind
takes the data (x and y) as well as the bandwidth
h and the binwidth d as inputs.
The bandwidth is visible in (12.7) but the binwidth d is not. This is because binning the data is merely a computational device for speeding up the computation of the estimator. Larger binwidth will speed up computation but imply a loss in information (due to using binned data rather than the actual data) that may be prohibitively large.
You may wonder what happened to the trimming bounds ![]() in
(12.7).
Trimming is necessary for working out the theoretical properties of the
estimator (to control the random denominator of
in
(12.7).
Trimming is necessary for working out the theoretical properties of the
estimator (to control the random denominator of
![]() ). In
). In
 adeind
, the trimming bounds are implicitly set such that 5 % of the data are
always trimmed off at the boundaries (this is done by calling
adeind
, the trimming bounds are implicitly set such that 5 % of the data are
always trimmed off at the boundaries (this is done by calling
 trimper
within
trimper
within
 adeind
;
adeind
;
 trimper
is an auxiliary quantlet, not covered here
in more detail).
trimper
is an auxiliary quantlet, not covered here
in more detail).
In the following example, simulated data are used to illustrate the
use of
 adeind
:
adeind
:
library("metrics")
randomize(333)
n = 500
x = normal(n,3)
beta = #(0.2 , -0.7 , 1)
index = x*beta
eps = normal(n,1) * sqrt(0.5)
y = 2 * index^3 + eps
d = 0.2
m = 5
{delta,dvar} = adeind(x,y,d,m)
(delta/delta[1])~(beta/beta[1])
Contents of _tmp [1,] 1 1 [2,] -4.2739 -3.5 [3,] 5.8963 5Note that this example does not work in the Academic Edition of XploRe .
The need for trimming in ADE is a consequence of its random
denominator. This and other difficulties associated with a random denominator
are overcome by the Density Weighted Average Derivative Estimator (DWADE) of
Powell, Stock and Stoker (1989). It is based on the density weighted
average derivative of ![]() with respect to
with respect to ![]() :
:
It can be shown that
| (12.9) |
 dwade
quantlet:
dwade
quantlet:
d = dwade(x, y, h)
 dwade
needs the data (x and y and the bandwidth
h as inputs and returns the vector of estimated
density weighted average derivatives.
dwade
needs the data (x and y and the bandwidth
h as inputs and returns the vector of estimated
density weighted average derivatives.
We illustrate
 dwade
with simulated data:
dwade
with simulated data:
library("metrics")
randomize(333)
n = 500
x = normal(n,3)
beta = #(0.2 , -0.7 , 1)
index = x*beta
eps = normal(n,1) * sqrt(0.5)
y = 2 * index^3 + eps
h = 0.3
d = dwade(x,y,h)
(d/d[1])~(beta/beta[1])
Contents of _tmp [1,] 1 1 [2,] -3.4727 -3.5 [3,] 4.9435 5
By definition, derivatives can only be calculated for continuous variables. Thus,
 adeind
and
adeind
and
 dwade
will not produce estimates of the components
of
dwade
will not produce estimates of the components
of ![]() that belong to discrete explanatory variables.
that belong to discrete explanatory variables.
Most discrete explanatory variables are 0/1 dummy variables. How do they
enter into SIMs ?
To give an answer, let us assume that ![]() consists of several continuous and a
single dummy variable and let us split
consists of several continuous and a
single dummy variable and let us split ![]() and
and ![]() accordingly into
accordingly into ![]() (continuous component) and
(continuous component) and ![]() (dummy), and
(dummy), and ![]() and
and ![]() respectively.
Then we have
respectively.
Then we have
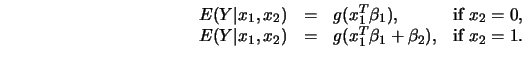
This is the basic idea underlying the estimator of ![]() proposed by
Horowitz and Härdle (1996): given an estimate of
proposed by
Horowitz and Härdle (1996): given an estimate of ![]() (which can be obtained
by using
(which can be obtained
by using
 dwade
, for instance) we can estimate both curves in
Figure 12.1 by running separate kernel regression of
dwade
, for instance) we can estimate both curves in
Figure 12.1 by running separate kernel regression of ![]() on
on
![]() for
the data points for which
for
the data points for which ![]() (to get an estimate of
(to get an estimate of
![]() )
and for which
)
and for which ![]() (to get an estimate of
(to get an estimate of
![]() ). Then we can compute
the horizontal differences between the two estimated curves to get an estimate
of
). Then we can compute
the horizontal differences between the two estimated curves to get an estimate
of ![]() This procedure is implemented in the
XploRe
quantlet
This procedure is implemented in the
XploRe
quantlet
 adedis
:
adedis
:
{d, a, lim, h} = adedis(x2, x1, y, hd, hfac,c0,c1)
It takes as inputs the data, consisting of x2 (discrete explanatory variables),
x1 (continuous explanatory variables) and y, and several parameters that
are needed in the three steps of
 adedis
estimation:
adedis
estimation:
 dwade
. Separate
estimates of
dwade
. Separate
estimates of 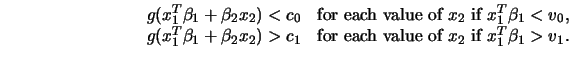
 adedis
essentially calculates the horizontal differences
between the estimated
adedis
essentially calculates the horizontal differences
between the estimated
Whereas you have to specify ![]() and
and ![]() the constants
the constants ![]() and
and ![]() are
implicitly set to the minimum and maximum of
are
implicitly set to the minimum and maximum of
![]() , plus or
minus the bandwidth used in the kernel estimation of
, plus or
minus the bandwidth used in the kernel estimation of
![]() The values of
The values of
![]() and
and ![]() are returned by
are returned by
 adedis
in the vector lim, along
with the bandwidth
adedis
in the vector lim, along
with the bandwidth ![]() calculated according to (12.11.) The most
important outputs are, of course, the estimates of
calculated according to (12.11.) The most
important outputs are, of course, the estimates of ![]() and
and ![]() which are stored in d and a, respectively.
which are stored in d and a, respectively.
|
In the previous sections, we have seen that even the noniterative estimators of SIMs implemented in XploRe require quite a bit of care and computational effort. More importantly, semiparametric estimators are less efficient than parametric estimators if the assumptions underlying the latter are satisfied. It is therefore desirable to know whether the distributional flexibility of these models justifies the loss in efficiency and the extra computational cost. That is, we would like to statistically test semiparametric SIMs against easily estimable parametric SIMs.
Horowitz and Härdle (1994) have developed a suitable test procedure that
is implemented in the
 hhtest
quantlet.
Formally, the HH-test considers the following hypotheses:
hhtest
quantlet.
Formally, the HH-test considers the following hypotheses:
Here is the main idea underlying the HH-test:
if the model under the null is true (and given an estimate of ![]() ), then a
nonparametric regression of
), then a
nonparametric regression of ![]() on
on
![]() will give a consistent
estimate of the parametric function
will give a consistent
estimate of the parametric function
![]() . If, however, the parametric
model is wrong, then the nonparametric regression of
. If, however, the parametric
model is wrong, then the nonparametric regression of
![]() on
on
![]() will
deviate systematically from
will
deviate systematically from
![]()
This insight is reflected in the HH-test statistic:
The HH-test statistic is computed by the
XploRe
quantlet
 hhtest
:
hhtest
:
{t, p} = hhtest(vhat, y, yhat, h {,c {,m}}})
The function
 hhtest
takes as inputs
hhtest
takes as inputs
 glmest
with the "bipro" option on your data. See
GLM (7).
glmest
with the "bipro" option on your data. See
GLM (7).
 hhtest
returns the test statistic t and the corresponding
hhtest
returns the test statistic t and the corresponding ![]() -value
p. Under
-value
p. Under ![]() the test statistic defined in (12.12) is asymptotically
normally distributed with zero mean and finite variance. The test, however, is
a one-sided test because deviations of
the test statistic defined in (12.12) is asymptotically
normally distributed with zero mean and finite variance. The test, however, is
a one-sided test because deviations of ![]() of the semiparametric kind considered in
(12.12) will lead to large positive values of the test statistic.
of the semiparametric kind considered in
(12.12) will lead to large positive values of the test statistic.
We illustrate
 hhtest
using the
kyphosis
data:
hhtest
using the
kyphosis
data:
library("metrics")
x = read("kyphosis")
y = x[,4]
x = x[,1:3]
x = matrix(rows(x))~x
h = 2
g = glmbilo(x,y)
eta = x*g.b
mu = g.mu
{t,p} = hhtest(eta,y,mu,h,0.05,1)
t~p
Contents of _tmp [1,] -0.79444 0.21346The null hypothesis is the Logit model that was used to fit the data. We cannot reject