The proof of this proposition (3.1.1)
follows a technique used by
Parzen (1962) in the setting of density estimation.
Recall the definition of the kernel weights,
Consider the denominator and numerator separately. I show that
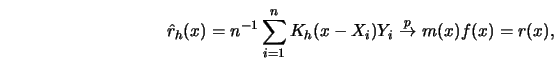 |
(3.3.14) |
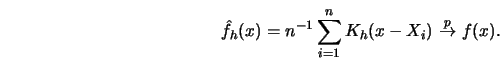 |
(3.3.15) |
From (3.1.9) and (3.3.15) it follows by Slutzky's Theorem
Schönfeld (1969, Chapter 6), that
Only (3.3.14) is shown; the statement (3.3.15) can be proved very
similarly.
Note that
where 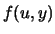 denotes the joint density of the distribution of
denotes the joint density of the distribution of 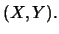 Conditioning on
Conditioning on 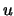 gives
gives
since
Using integration by substitution it can be shown (see Lemma
3.1 in these
Complements) that for 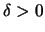
The last two terms of this bound tend to zero, by (A1) and (A2), as
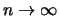 .
Now let
.
Now let 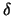 tend to zero; then the first term
by continuity of
tend to zero; then the first term
by continuity of 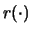 will tend to zero.
This proves that
will tend to zero.
This proves that
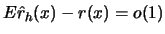 , as
, as 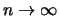 .
Now let
.
Now let
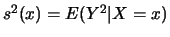 . Use integration by substitution and the
above asymptotic unbiasedness of
. Use integration by substitution and the
above asymptotic unbiasedness of 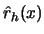 to see that the variance
of
to see that the variance
of 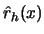 is
is
This is asymptotically equal to
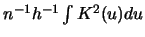
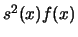 using the techniques of splitting up the same
integrals as above.
Observe now that the variance tends to zero as
using the techniques of splitting up the same
integrals as above.
Observe now that the variance tends to zero as 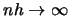 . This
completes the argument since the mean squared error
. This
completes the argument since the mean squared error
![$E(\hat r_h(x)-r(x))^2 = var(\hat r_h(x)) + [E\hat r_h(x)-r(x)]^2 \to 0$](anrhtmlimg389.gif) as
as
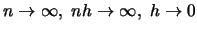 .
Thus we have seen that
.
Thus we have seen that
This implies
(see Schönfeld; 1969, chapter 6) proof can be adapted to kernel estimation with higher
dimensional  .
If
.
If  is
is 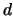 -dimensional, change
-dimensional, change 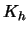 to
to 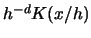 , where
, where 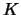 :
:
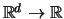 and the ratio in the argument of
and the ratio in the argument of  has to be understood coordinatewise.
has to be understood coordinatewise.
LEMMA 3.1
The estimator
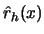
is asymptotically unbiased
as an estimator
for
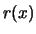
.
Use integration by substitution and the fact that the kernel integrates
to one to bound
The first term can be bounded in the following way:
The third term
The second term can be bounded as follows:
Note that the last integral exists by assumption (A3) of Proposition
3.1.1
The derivative estimator
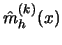 is asymptotically
unbiased.
is asymptotically
unbiased.
using partial integration, (A0) and (A4).
The variance of
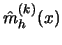 tends to zero if
tends to zero if
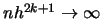 , as the following calculations show:
, as the following calculations show:
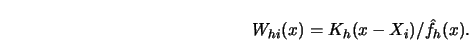
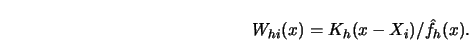
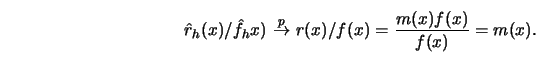
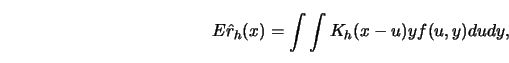

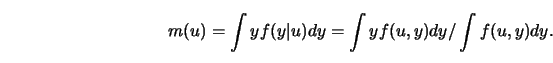
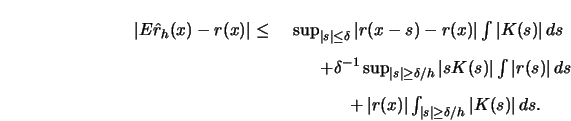
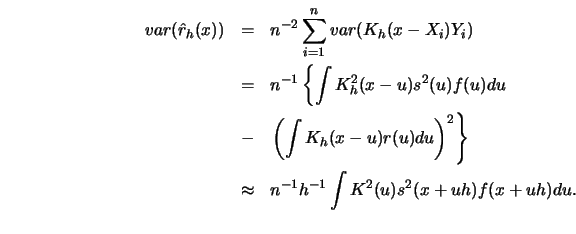
![]()
![]() using the techniques of splitting up the same
integrals as above.
Observe now that the variance tends to zero as
using the techniques of splitting up the same
integrals as above.
Observe now that the variance tends to zero as ![]() . This
completes the argument since the mean squared error
. This
completes the argument since the mean squared error
![]() as
as
![]() .
Thus we have seen that
.
Thus we have seen that


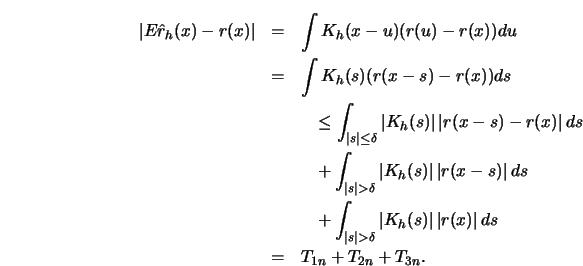
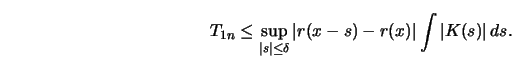

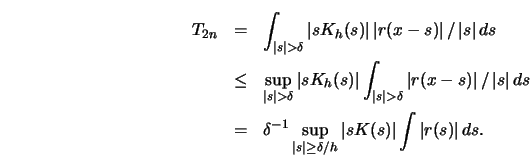
![]() is asymptotically
unbiased.
is asymptotically
unbiased.
![]() tends to zero if
tends to zero if
![]() , as the following calculations show:
, as the following calculations show: