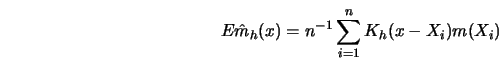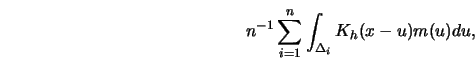Near the boundary of the observation interval any smoothing method will become
less accurate. At the boundary fewer observations can be averaged and thus
variance or bias can be affected. Consider kernel weights; they become
asymmetric as 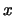 approaches the boundary points. This ``boundary effect'' is
not present for
approaches the boundary points. This ``boundary effect'' is
not present for 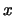 in the interior of the observation interval, but for a
small to moderate sample size, a significant proportion of the observation
interval can be affected by the boundary behavior. Consider, for instance, the
kernel smooth in Figure 3.2. The Gaussian kernel that has been used there is
always truncated through boundary points. The whole observation interval is
thus in a (strict) sense influenced by boundary effects. Note, however, that
this kernel is effectively zero outside the range of three standard
deviations, so a smaller proportion of the observations on each side are due
to boundary effects.
in the interior of the observation interval, but for a
small to moderate sample size, a significant proportion of the observation
interval can be affected by the boundary behavior. Consider, for instance, the
kernel smooth in Figure 3.2. The Gaussian kernel that has been used there is
always truncated through boundary points. The whole observation interval is
thus in a (strict) sense influenced by boundary effects. Note, however, that
this kernel is effectively zero outside the range of three standard
deviations, so a smaller proportion of the observations on each side are due
to boundary effects.
In this section I describe the boundary effects and present a simple and
effective solution to the boundary problem. This solution is due to Rice
(1984b) and uses the (generalized) jackknifing technique. Boundary phenomena
have also been discussed by Gasser and Müller (1979) and Müller (1984b)
who proposed ``boundary kernels'' for use near the boundary. In the setting of
spline smoothing Rice and Rosenblatt (1983) computed the boundary bias.
Consider the fixed design error model with kernels having support ![$[-1,1]$](anrhtmlimg222.gif) .
Take the kernel estimator
.
Take the kernel estimator
which has expectation equal to (see Exercise 4.4)
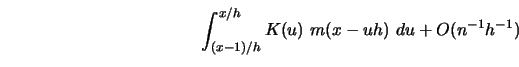 |
(4.4.21) |
as
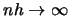 . In the middle of the observation interval there is no
problem since for
. In the middle of the observation interval there is no
problem since for 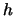 small,
small, 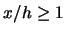 and
and 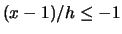 .
.
Now let
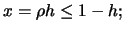 then by a Taylor series expansion the expected
value of
then by a Taylor series expansion the expected
value of
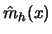 can be approximated by
can be approximated by
Of course, if 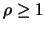 ,
,
and we have the well-known bias expansion for the Priestley-Chao estimator.
The idea of John Rice is to define a kernel depending on the relative location
of 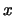 expressed through the parameter
expressed through the parameter 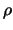 .
.
Asymptotic unbiasedness is achieved for a kernel
If 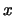 is away from the left boundary, that is,
is away from the left boundary, that is, 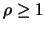 , then the
approximate bias is given by the third term. If
, then the
approximate bias is given by the third term. If 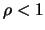 , the second term is of
dominant order
, the second term is of
dominant order 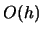 and thus the bias is of lower order at the boundary than
in the center of the interval.
and thus the bias is of lower order at the boundary than
in the center of the interval.
The generalized jackknife technique (Gray and Schucany 1972) allows one to
eliminate this lower order bias term. Let
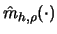 be the kernel
estimator with kernel
be the kernel
estimator with kernel 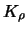 and let
and let
be the jackknife estimator of 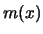 , a linear combination of kernel
smoothers with bandwidth
, a linear combination of kernel
smoothers with bandwidth 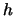 and
and 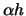 . From the bias expansion
4.4.22,
the leading bias term of
. From the bias expansion
4.4.22,
the leading bias term of
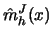 can be eliminated if
can be eliminated if
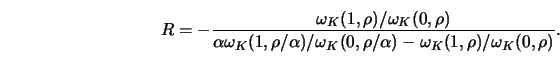 |
(4.4.23) |
This technique was also used by Bierens (1987) to reduce the bias inside the
observation interval. In effect, the jackknife estimator is using the kernel
function
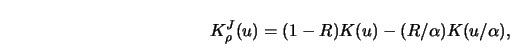 |
(4.4.24) |
where 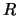 and
and 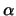 and thus
and thus 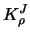 depend on
depend on 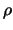 . In this sense,
. In this sense,
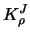 can be interpreted as a ``boundary kernel''. Rice (1984b) has
recommended the following for the choice of
can be interpreted as a ``boundary kernel''. Rice (1984b) has
recommended the following for the choice of 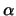 :
:
As an example, take as the initial kernel the quartic kernel
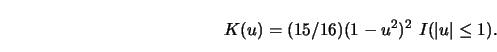 |
(4.4.25) |
The numbers
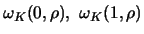 can be computed explicitly.
Figure 4.11 shows the sequence of boundary kernels
can be computed explicitly.
Figure 4.11 shows the sequence of boundary kernels 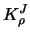 for
for
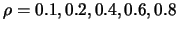 . Note that the kernels have negative side lobes.
Figure 4.12 shows the nonparametric estimate of the function
. Note that the kernels have negative side lobes.
Figure 4.12 shows the nonparametric estimate of the function 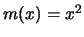 from
from
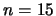 observations (Gaussian noise,
observations (Gaussian noise, 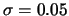 ). The bandwidth
). The bandwidth 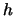 is
is
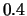 , thus
, thus 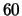 percent of the observation interval are due to boundary effects.
percent of the observation interval are due to boundary effects.
Figure 4.11:
Modified quartic boundary kernels 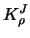 for
for
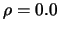 , 0.2, 0.4, 0.6, 0.8. The symmetric kernel is the kernel
, 0.2, 0.4, 0.6, 0.8. The symmetric kernel is the kernel 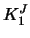 .
From Rice (1984b) with permission of Marcel Dekker, Inc., New York.
.
From Rice (1984b) with permission of Marcel Dekker, Inc., New York.
|
|
Exercises
4.4.1 Compute the constants
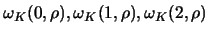 from 4.4.22 for the quartic kernel. Construct an algorithm
with bias correction at the boundary.
from 4.4.22 for the quartic kernel. Construct an algorithm
with bias correction at the boundary.
[Hint: The system XploRe (1989) contains this algorithm for the
triweight kernel.]
4.4.2 Proof formula 4.4.21 by comparing
with
where
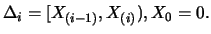
![]() .
Take the kernel estimator
.
Take the kernel estimator
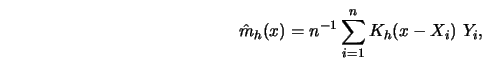
![]() then by a Taylor series expansion the expected
value of
then by a Taylor series expansion the expected
value of
![]() can be approximated by
can be approximated by


![]() be the kernel
estimator with kernel
be the kernel
estimator with kernel ![]() and let
and let
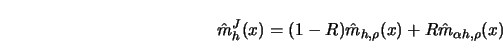

![\includegraphics[scale=0.2]{ANR4,11.ps}](anrhtmlimg1302.gif)
![\includegraphics[scale=0.2]{ANR4,12.ps}](anrhtmlimg1305.gif)
![]() from 4.4.22 for the quartic kernel. Construct an algorithm
with bias correction at the boundary.
from 4.4.22 for the quartic kernel. Construct an algorithm
with bias correction at the boundary.