8.1 Monotonic and unimodal smoothing

The problem of monotonic smoothing on a set $\{(X_i, Y_i) \}^n_{i=1}$ of two-dimensional data can be formalized as follows. Sort the data $\{(X_i, Y_i) \}^n_{i=1}$ by $X$ into $\{(X_{(i)}, Y_{(i)})\}^n_{i=1}.$ Find $\{ \hat m(X_{(i)})\}^n_{i=1}$ to minimize $n^{-1}\sum_{i=1}^n ( Y_{(i)}-\hat m(X_{(i)}) )^2$ subject to the monotonicity restriction

$$\hat m(X_{(1)})\le \hat m(X_{(2)})\le \cdots \le \hat m(X_{(n)}).$$

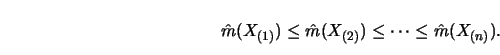
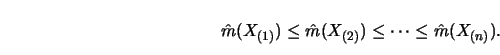
Such a solution exists and can be obtained from the pool adjacent violators algorithm, (Barlow et al. 1972, p. 13; Hanson, Pledger and Wright 1973). The pool-adjacent-violators algorithm (from the left) can be formalized as follows.

8.1.1 Pool-adjacent-violators (PAV) Algorithm

Algorithm 8.1.1
STEP 1.

Start with $Y_{(1)},$ move to the right and stop if the pair
$(Y_{(i)}, Y_{(i+1)})$ violates the monotonicity constraint, that is,
$Y_{(i)} > Y_{(i+1)}.$ Pool $Y_{(i)}$ and the adjacent $Y_{(i+1)},$ by replacing them
both by their average,

$$Y_{(i)}^* = Y^*_{(i+1)}=(Y_{(i)}+Y_{(i+1)})/2\ .$$

STEP 2.

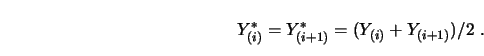
Next check that $Y_{(i-1)}\le Y^*_{(i)}$. If not, pool $\{ Y_{(i-1)}, Y_{(i)}, Y_{(i+1)}\}$ into
one average. Continue to the left until the monotonicity
requirement is satisfied. Then proceed to the right. The final
solutions are $\hat m(X_{(i)}).$

There are four remarkable facts about this solution. First, if the data are already monotone, then the PAV algorithm will reproduce the data. Second, since each $\hat m(X_{(i)})$ is an average of the observations near $X_{(i)}$ the solution is a step function as in Figure 8.1. Third, if there are outliers or aberrant observations the PAV algorithm will produce long, flat levels. Fourth, suppose the algorithm is started from the right with the aim of pooling to obtain a decreasing fit (looking from the right). The fits starting from left and right are different (Exercise 8.1.1). Especially the third fact about outlier dependence could be treated by first smoothing (with a robust technique) and then isotonizing the smooth. On the other hand, one could also first apply the PAV algorithm and then smooth the solution. Hildenbrand and Hildenbrand (1986) applied the first strategy in nonparametric estimation of Engel curves. Figure 8.1 shows a spline smooth and a PAV smooth obtained from estimating the Engel curve of food as a function of income.

On the contrary, Friedman and Tibshirani (1984) proposed smoothing the data first and then searching for a monotone approximation of the smooth. This second algorithm can be summarized as follows. First, smooth $Y$ on $X$, that is, produce an estimate $\hat m_1(X_{(i)})$ with a cross-validated smoothing parameter. Second, find the monotone function $\hat m(X_{(i)})$ closest to $\hat m_1(X_{(i)})$ by means of the PAV algorithm. Friedman and Tibshirani (1984) gave an example of this algorithm to find an optimal transformation for a nonparametric version of the Box-Cox procedure (1964).

Figure 8.1: A spline smooth through the midpoints of the PAV step function. The isotonic regression curve was computed from the food versus income data set. (Family Expenditure Survey 1968-1983). From Hildenbrand and Hildenbrand (1986) with permission of Elsevier Science Publishers .

Kelly and Rice (1988) used monotone smoothing in a similar model for assessment of synergisms. The goal of the nonparametric Box-Cox procedure is to identify the smooth monotone link function $\theta(\cdot)$ and the parameter $\beta$ in the model

$$\theta(Y) = \beta^T X+\varepsilon.$$

This can be achieved by finding a function $\hat \theta(\cdot)$ and an estimate $\hat\beta$ that minimize

$$n^{-1}\sum_{i=1}^n ( \hat \theta (Y_i) -\hat \beta^TX_i )^2$$

subject to

$$n^{-1}\sum_{i=1}^n \left( \hat \theta(Y_i) - n^{-1}\sum_{j=1}^n \hat\theta(Y_j) \right)^2 = 1.$$

Note that this procedure is a special case of the ACE algorithm (Section 10.3), which consists of finding $\hat\beta$ for fixed $\hat \theta(\cdot)$ and vice versa.

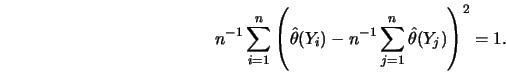
The Box-Cox procedure and a method proposed by Kruskal (1965) are variants of this procedure. The Box-Cox procedure consists of using the parametric transformation family

$$g_{\lambda}(Y)=\left\{\begin{array}{ll} (Y^{\lambda} - 1)/\l... ...da >0; \\ \log Y, &{\rm if}\ \lambda =0, \end{array}\right.$$ (8.1.1)

to model the unknown function $\theta(\cdot)$. Kruskal used isotonic regression (by the PAV algorithm) to estimate $\theta(\cdot)$. Friedman and Tibshirani applied the nonparametric procedure to the same data and showed that the monotone smooth transformation $\hat \theta(\cdot)$ came remarkably close to the log-transformation selected by Box and Cox (1964); see Figure 8.2.

Figure 8.2: The monotone smooth selected by the Friedman-Tibshirani algorithm and the log-transformation. From Friedman and Tibshirani (1984) with permission of the American Statistical Association.

Figure 8.3 shows the result of Kruskal's algorithm together with the log-transformation. The transformation suggested by the Kruskal method by construction lacks smoothness, whereas the monotone smooth gives evidence for a log-transformation; see Figure 8.3.

It is, of course, interesting to ask which method is to be preferred in which situation. Should we smooth first and then isotonize the smooth via the PAV algorithm or should we apply the PAV algorithm first and then smooth? Mammen (1987) investigated this question in the fixed design model. His theoretical comparison is given in more detail in the Complements to this section. It is remarkable from Mammen's results that neither method outperforms the other. More precisely, isotonizing the observations first leads to a smaller variance and a larger bias. The Friedman-Tibshirani method can have a smaller MSE but conditions when this will happen are rather complicated and depend on the unknown regression function.

Figure 8.3: The result of the Kruskal algorithm and the log-transformation. From Friedman and Tibshirani (1984) with permission of the American Statistical Association.

Variants of the above methods are monotone median and percentile regression. They have been investigated by Cryer et al. (1972) and Casady and Cryer (1976). Two-dimensional isotonic smoothing is given as algorithm AS 206 in Bril et al. (1984).

The problem of unimodal smoothing can be related to monotone smoothing. Suppose that $m(x)$ has a mode at $x=\alpha$. This means that

$$x_1 \le x_2 \le \alpha\; \Rightarrow\; m(x_1) \le m(x_2)$$

and

$$\alpha \le x_1 \le x_2\; \Rightarrow\; m(x_1) \ge m(x_2)).$$

Then the function

$$g(x) =\left \{\begin{array}{ll} 2m(\alpha)- m(x), &{\rm if}... ...\alpha; \\ m(x), &{\rm if} \ x \le \alpha, \end{array}\right.$$

is monotone.

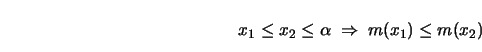
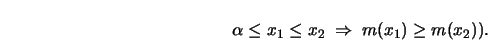
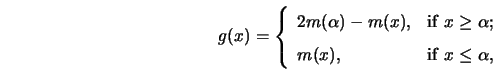
(The problem of ``U-shaped regression" can be defined analogously by smoothing $-g(x)$.) A possible way of finding an unimodal smooth is to mirror the observations at possible mode points and then to find a monotone smooth of the partially mirrored data.

More formally, the unimodal regression problem is to find a smooth which minimizes $n^{-1}\sum_{i=1}^n ( Y_{(i)}-\hat m(X_{(i)}) )^2$ subject to the restrictions:

$$X_{(i)}\le X_{(j)} \le X_{(k)}\ \Rightarrow \ \hat m(X_{(i)}) \le \hat m(X_{(j)})$$

and

$$X_{(k)} < X_{(i)} \le X_{(j)}\ \Rightarrow \ \hat m(X_{(i)}) \ge \hat m(X_{(j)})$$

for some $k$.

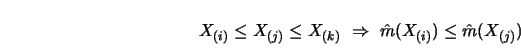
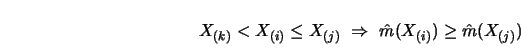
Frisén and Goteborg (1980) proposed treating the index $k$ as a parameter, and then, solving for each $k$, a monotone increasing smoothing problem for the data $\{ (X_{(i)}, Y_{(i)})\}^k_{i=1}$ and a monotone decreasing smoothing problem for the data $\{ (X_{(i)}, Y_{(i)})\}^n_{i=k+1}$. Then one chooses the empirical mode $X_{(k)}$ that leads to the lowest residual sum of squares.

Hildenbrand and Hildenbrand (1986) report that the above algorithm tends to produce a spike at $X_{(k)}$. For this reason it makes sense to first estimate the mode by $\hat \alpha = \arg\max [ \hat m(x)]$ in a ``presmoothing step." In a second step, one then considers unimodal regression with pre-estimated mode $\hat \alpha$ by mirroring the right half of the data at the empirical mode $\hat \alpha.$ This algorithm has been applied to the potato versus net income example; see Figure 8.4.

Figure 8.4: Unimodal regression for the potato versus net income example. The points indicate the unimodal regression and the solid line a spline smooth of the unimodal regression step function. From Hildenbrand and Hildenbrand (1986) with permission of Elsevier Science Publishers.

Exercises

8.1.1 (by Kurt Hildenbrand)

Consider the following algorithm for PAV smoothing. The input is contained in Y[1$\ldots \$N], the isotonic output in R[1$\ldots \$ N]. Explain the role of the vector NEXT(I)!

DO I$=$ N TO 1 by -1;

R(I) $=$ Y(I); NEXT(I) $=$ I+1;

DO WHILE (NEXT(I) $<=$ N) IF R(I)*(NEXT(NEXT(I))-NEXT(I))

$<$ R(NEXT(I))*(NEXT(I)$-I$) THEN LEAVE; (this loop)

R(I) $=$ R(I) + R(NEXT(I));

NEXT(I) $=$ NEXT(NEXT(I));

END;

END;

DO I $=$ 1 REPEAT NEXT(I) UNTIL (NEXT(I) $>$ N );

IF NEXT(I)-I $>$ 1 THEN DO;

R(I) $=$ R(I)/(NEXT(I)-I);

DO I1 $=$ I + 1 TO NEXT(I)$-1$; R(I1) $=$ R(I); END;

END;

END;

8.1.2Explain qualitatively when you would like to prefer to smooth first and then to isotonize.

8.1.3Calculate the asymptotic MSE from Theorem 8.1.1 in the Complements to this section.

8.1.4Use an asymptotic MSE optimal bandwidth $h_0$ in 8.1.5. How does the condition then look?

8.1.5Rewrite the PAV algorithm so that it starts from the right and does pooling while descending. Why is the answer, in general, different from the fit starting from the left?

8.1.2 Complements

Let me compare the two proposed methods

30pt to 30ptSISmooth first then Isotonize ,

30pt to 30ptISIsotonize first then Smooth .

Consider the fixed design case. Let $\hat m_h(x)$ denote the Priestley-Chao kernel estimator and $\hat m_h^{IS}(x), \hat m_h^{SI}(x)$ the variants of it according to the above two methods. Mammen (1987) showed the following theorem.

Theorem 8.1.1   Assume that

30pt to 30pt(A1) $X_i = i/n, \ i = 0, \pm 1, \ldots, \pm n$,

30pt to 30pt(A2) $E (\exp (t \varepsilon_i)) < \infty$ for $t$ small enough,

30pt to 30pt(A3) $m \in {\cal C}^2$, $m' \ge 0$, $\ x \in [-1, 1]$, $m'(0) > 0$.

Then

$$\hat m_h^{SI}(0) = \hat m_h(0) + o_p(1/n).$$ (8.1.2)

Furthermore, there exist independent random mean zero variables $U_{1n}, U_{2n}$ such that for some universal constants $c_1, c_2, c_3$ the following expansions hold.

$$\hat m_h^{SI}(0) = \beta_n + U_{1n} + o_p(n^{-2/3}),$$ (8.1.3)

$$\hat m_h^{IS}(0) = \beta_n + \delta_n + (1- \eta_n) U_{1n} + U_{2n} + o_p(n^{-2/3}),\quad$$ (8.1.4)

where

$$\begin{eqnarray*} \beta_n &=& (1/2) m''(0) d_K n^{-2/5},\cr \delta_n &=& c_3 \si... ...c_K^{(1)} c_K^{-1} n^{-4/15},\cr c_K^{(1)} &= &\int [K'(u)]^2 du.\end{eqnarray*}$$

Furthermore, $n^{2/5}U_{1n}$ and $n^{8/15}U_{2n}$ are asymptotically normal with variances $\sigma^2 c_K$ and $c_1 \sigma^{10/3} [m'(0)]^{-4/3} c_K^{(1)}$, respectively.

The theorem can be used to calculate the asymptotic MSE, see Exercise 8.1.1. Mammen reports that simulations show that $c_1 < 2 c_2$. Therefore, the method IS leads to a variance reduction and a larger bias. Furthermore, it can be computed from 8.1.38.1.4 that $\hat m_h^{IS}(0)$ has a smaller MSE than $\hat m_h^{SI}(0)$ if and only if

$${ h^5 d_K [m''(0)]^2 \over \sigma^2 c_K^{(1)} } < { 2c_2 - c_1 \over 2c_3 }\cdotp$$ (8.1.5)

The universal constants come from the technique used by Mammen, the approximation of the empirical distribution function by a sequence of Brownian bridges. It is very interesting that the asymptotic variance of $\hat m_h^{IS}(0)$ has a second-order term of the order $O(n^{-16/15})$, where the constant in this rate is negative and proportional to $[m'(0)]^{-4/3}$. This seems to be quite intuitive: If the slope at a point is not very steep we expect the ISmethod to behave better than the SI method. Certainly, if $m'(0)$ is small we can allow for a broad (random) bandwidth from the PAV algorithm.