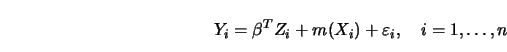9. Incorporating parametric components

                We must confine ourselves to those forms that we know how to handle, or for which any tables which may be necessary have been constructed.

Sir R.A. Fisher (1922)

For a pragmatic scientist the conclusion of Fisher (1922), to ``confine ourselves to those forms that we know how to handle, " must have an irresistible attractive power. Indeed, we know that the nonparametric smoothing task is hard, especially in high dimensions. So why not come back to parametrics, at least partially? A parametric together with a nonparametric component may handle the model building even better than just the nonparametric or the parametric approach! In this chapter I present approaches from both views. The discussed models incorporate both parametric and nonparametric components and are therefore called semiparametric models.

Three topics are addressed. First, the estimation of parameters in a partial linear model. Second, the comparison of individual curves in a shape-invariant context. Third, a method is proposed to check the appropriateness of parametric regression curves by comparison with a nonparametric smoothing estimator.

An example of a semiparametric model is

$$Y_i= \beta^T Z_i +m(X_i) + \varepsilon_i, \quad i=1, \ldots, n$$ (9.0.1)

where $\beta^T =(\beta_1, \ldots, \beta_p)$ is a $p$-vector of unknown regression coefficients and $m$: $\mathbb{R}^d\to \mathbb{R}$ is an unknown smooth regression function. Here the response $Y$ depends on a pair of predictor variables $(X,Z)$ such that the mean response is linear on $Z \in \mathbb{R}^p$ (parametric component) and possibly nonlinear on $X \in \mathbb{R}^d$ (nonparametric component). For the structure of its parametric component this model is called a partial linear model.

Another semiparametric model is motivated from growth curve analysis. In this setting one observes that individual curves differ but have the same general overall shape. More formally, suppose that at least two sets of regression data

$$Y_{ij} =m_j (X_{ij})+\varepsilon_{ij}, \quad i=1, \ldots, n, \ j=1, \ldots, J, \ J \ge 2,$$ (9.0.2)

have been observed and that each ``individual curve" $m_j( \cdot)$ is modeled nonparametrically. The same ``overall shape" of the curves $m_j$ can be expressed formally by the existence of transformations $S_{\theta}, T_{\theta}$ such that

$$m_j (x)=S^{-1}_{\theta_j} [ m_1 (T^{-1}_{\theta_j} (x)) ], \ j\ge 2.$$ (9.0.3)

The ``individual curves" $m_j$ are thus mapped into each other by means of certain parametric transformations. Examples of possible transformations are shift/scale families, that is,

$$m_j (x)= \theta_{3j} +\theta_{4j} m_1 ((x-\theta_{1j})/\theta_{2j}), \quad j \ge2,$$ (9.0.4)

where both $S_{\theta}$ and $T_{\theta}$ are of the form $(x-u)/v, \quad v \not= 0.$ Since with these specific transformations $S_{\theta}, T_{\theta}$ the shape of all individual curves $m_j( \cdot)$ is the same for all $j$, this model has also been called shape invariant.

As an example of a shape-invariant model consider the issue of constant demand Engel curves over time (Hildenbrand 1985). Figure 9.1 shows expenditure Engel curves for food as a function of income for five different years (1969, 1971, 1973, 1975, 1977). All the curves look similar except that they have different lengths which corresponds to the presence of inflation and price changes over years.

Figure 9.1: Expenditure Engel curves for food as a function of total expenditure. The shortest line is the curve for year 1969, the next curve is that for year 1971 and the longest is computed from data for year 1977. Family Expenditure Survey, Annual Base Tapes (1968-1983).

Inserting such a scaling parameter into the shape-invariant model makes it possible to test and to evaluate the evolution of Engel curves; see Härdle and Jerison (1988).

Some additive models for multivariate data, for example, projection pursuit, could - in a strict sense - be considered semiparametric as well. The main feature of these models though is the additivity of their components. This is the reason why these models are presented in a separate chapter on additive models; see Chapter 10.

In Section 9.1 I present some recent results on partial linear models. Section 9.2 of this chapter is devoted to shape-invariant modeling. Section 9.3 discusses the comparison of nonparametric versus parametric regression fitting through evaluation of the squared deviation between the two curves.