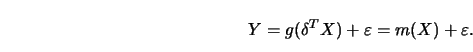While it is possible to encode several more dimensions into pictures by using time (motion), color, and various symbols (glyphs), the human perceptual system is not really prepared to deal with more than three continuous dimensions simultaneously.
Huber, P.J. (1985, p. 437)
The basic idea of scatter plot smoothing can be extended
to higher dimensions in a straightforward way.
Theoretically, the regression smoothing for a ![]() -dimensional predictor
can be performed as in the case of a one-dimensional predictor. The
local averaging procedure will still give asymptotically consistent
approximations to the regression surface. However, there are two major
problems with this approach to multiple regression smoothing. First,
the
regression function
-dimensional predictor
can be performed as in the case of a one-dimensional predictor. The
local averaging procedure will still give asymptotically consistent
approximations to the regression surface. However, there are two major
problems with this approach to multiple regression smoothing. First,
the
regression function ![]() is a high dimensional surface and since its
form cannot be displayed for
is a high dimensional surface and since its
form cannot be displayed for ![]() , it does not
provide a geometrical description of the regression relationship
between
, it does not
provide a geometrical description of the regression relationship
between ![]() and
and ![]() . Second, the basic element of nonparametric
smoothing - averaging over neighborhoods - will often be applied
to a relatively meager set of points since
even samples of size
. Second, the basic element of nonparametric
smoothing - averaging over neighborhoods - will often be applied
to a relatively meager set of points since
even samples of size ![]() are surprisingly
sparsely distributed in the higher dimensional Euclidean space.
The following two
examples by Werner Stuetzle exhibit this ``curse of dimensionality".
are surprisingly
sparsely distributed in the higher dimensional Euclidean space.
The following two
examples by Werner Stuetzle exhibit this ``curse of dimensionality".
A possible
procedure for estimating two-dimensional surfaces could be to
find the smallest rectangle with axis-parallel sides containing all
the predictor vectors and to lay down a regular grid on this rectangle.
This gives a total of one hundred cells if one cuts each side of a
two-dimensional rectangle into ten pieces. Each inner cell will have eight
neighboring cells. If one carried out this procedure in ten
dimensions there would be a total of
![]() cells
and each inner
cell would have
cells
and each inner
cell would have
![]() neighboring cells. In other words,
it will be hard to find neighboring observations in ten dimensions!
neighboring cells. In other words,
it will be hard to find neighboring observations in ten dimensions!
Suppose now one had ![]() points uniformly distributed over the ten
dimensional unit cube
points uniformly distributed over the ten
dimensional unit cube ![]() .
What is our chance of catching some points in a neighborhood of reasonable size
? An average over a neighborhood of diameter
.
What is our chance of catching some points in a neighborhood of reasonable size
? An average over a neighborhood of diameter ![]() (in each coordinate) results in a volume of
(in each coordinate) results in a volume of
![]() for the corresponding ten-dimensional cube.
Hence, the expected number of
observations in this cube will be
for the corresponding ten-dimensional cube.
Hence, the expected number of
observations in this cube will be
![]() and not
much averaging can be expected. If, on the other hand, one fixes the
count
and not
much averaging can be expected. If, on the other hand, one fixes the
count ![]() of observations over which to average, the diameter
of the typical (marginal)
neighborhood will be larger than
of observations over which to average, the diameter
of the typical (marginal)
neighborhood will be larger than ![]() which means
that the average is extended
over at least two-thirds of the range along each coordinate.
which means
that the average is extended
over at least two-thirds of the range along each coordinate.
A first view of the sparsity of high dimensional data
could lead one to the conclusion that one is
simply in a hopeless situation - there is just not enough clay to make
the bricks! This first view, however, is, as many first views are, a little
bit too rough. Assume, for
example, that the ten-dimensional regression surface is only
a function of ![]() , the first coordinate of
, the first coordinate of ![]() , and constant in all other
coordinates. In this case the ten-dimensional surface
collapses down to a one-dimensional problem. A similar conclusion holds
if the regression surface is a function only of certain linear combinations
of the coordinates of the predictor variable.
The basic idea of additive models is to take advantage of the fact that a
regression surface may be of a simple, additive structure.
, and constant in all other
coordinates. In this case the ten-dimensional surface
collapses down to a one-dimensional problem. A similar conclusion holds
if the regression surface is a function only of certain linear combinations
of the coordinates of the predictor variable.
The basic idea of additive models is to take advantage of the fact that a
regression surface may be of a simple, additive structure.
A regression tree is based on such a structure. The regression
surface is approximated by a linear combination of step functions

Another
additive model is projection pursuit regression (PPR) (Friedman
and Stuetzle 1981). This model is an extension of the regression tree model
and is defined through projections
![]() .
It models the regression surface as
.
It models the regression surface as

PPR involves one-dimensional nonparametric functions on linear combinations of predictor variables, whereas the alternative ACE-model determines a linear combination of nonparametric one-dimensional functions operating on the coordinates of the predictor variable with unknown possibly nonlinear transformations; see Section 10.3.
The last technique considered here is related to PPR,