The primary motivation for studying the average derivative
with
comes from models where the mean response depends on 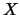 only
through a linear combination
only
through a linear combination 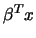 . That is, similarly to
projection pursuit regression,
. That is, similarly to
projection pursuit regression,
 |
(10.4.9) |
for some nonparametric function 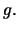
The average derivative 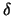 is proportional to
is proportional to 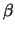 since
since
Thus the average derivative vector 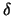 determines
determines 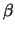 up to scale.
In this section a nonparametric estimator
up to scale.
In this section a nonparametric estimator 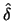 of the average
derivative is considered which achieves the rate
of the average
derivative is considered which achieves the rate 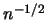 (typical for parametric problems).
From this
(typical for parametric problems).
From this 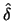 the multivariate
the multivariate
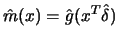 is constructed which achieves the rate
is constructed which achieves the rate
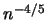 (typical for one dimensional smoothing problems). A weighted
average derivative estimator has been introduced by Powell, Stock and Stoker
(1989).
(typical for one dimensional smoothing problems). A weighted
average derivative estimator has been introduced by Powell, Stock and Stoker
(1989).
Assume that the function
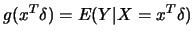 is
normalized in such a way that
is
normalized in such a way that
![$E[ d g / d(x^T\delta)] =1.$](anrhtmlimg2753.gif) Average derivative estimation(ADE) yields a
direct estimator for the weights
Average derivative estimation(ADE) yields a
direct estimator for the weights 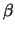 in 10.4.9.
(Note that as in PPR the model 10.4.9 is not identifiable unless we make
such a normalization assumption.)
in 10.4.9.
(Note that as in PPR the model 10.4.9 is not identifiable unless we make
such a normalization assumption.)
Let  denote the marginal density,
denote the marginal density,
its vector of partial derivatives and
the negative log-density derivative. Integration by parts gives
![\begin{displaymath}
\delta = E[ m'(X)] = E[ l Y].
\end{displaymath}](anrhtmlimg2756.gif) |
(10.4.10) |
Consequently, if  denotes a kernel estimator
of
denotes a kernel estimator
of 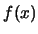 and
and
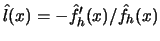 , then
, then 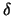 can be estimated by the sample analogue
can be estimated by the sample analogue
Since this estimator involves dividing by 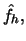 a more refined estimator
a more refined estimator 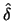 of
of 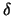 is advisable in practice.
For this reason the following estimator is proposed:
is advisable in practice.
For this reason the following estimator is proposed:
 |
(10.4.11) |
with the indicator variables
and the density estimator
Note that here the kernel function 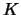 is a function of
is a function of 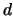 arguments. Such a kernel can be constructed, for example,
as a product of one-dimensional kernels; see Section 3.1. The main result of
Härdle and Stoker (1989) is Theorem 10.4.1.
arguments. Such a kernel can be constructed, for example,
as a product of one-dimensional kernels; see Section 3.1. The main result of
Härdle and Stoker (1989) is Theorem 10.4.1.
Theorem 10.4.1
Assume that apart from very technical conditions,
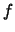
is
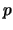
-times
differentiable,
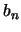
``slowly"
converges to zero and
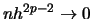
, where
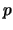
denotes the number of derivatives of
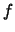
.
Then the average derivative estimator
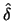
has a limiting
normal distribution,
where
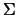
is the covariance matrix of
There are some remarkable features about this result. First, the
condition on the bandwidth sequence excludes the optimal bandwidth
sequence
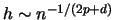 ; see Section 4.1.
The bandwidth
; see Section 4.1.
The bandwidth 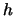 has to tend to zero
faster than the optimal rate in order to keep the bias of
has to tend to zero
faster than the optimal rate in order to keep the bias of
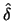 below the desired
below the desired 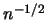 rate. A similar
observation has been made in the context of semiparametric models;
see Section 8.1. Second, the covariance matrix is constructed from
two terms,
rate. A similar
observation has been made in the context of semiparametric models;
see Section 8.1. Second, the covariance matrix is constructed from
two terms, 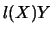 and
and
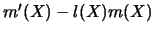 . If one knew the
marginal density then the first term
. If one knew the
marginal density then the first term 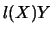 would
determine the covariance. It is the estimation of
would
determine the covariance. It is the estimation of
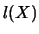 by
by 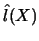 that brings in this second term. Third, the
bandwidth condition is of qualitative nature, that is, it says that
that brings in this second term. Third, the
bandwidth condition is of qualitative nature, that is, it says that 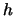 should
tend to zero not ``too fast" and not ``too slow."
A more refined analysis
(Härdle, Hart, Marron and Tsybakov 1989) of
second-order terms shows that for
should
tend to zero not ``too fast" and not ``too slow."
A more refined analysis
(Härdle, Hart, Marron and Tsybakov 1989) of
second-order terms shows that for 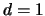 the MSE of
the MSE of 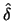 can be
expanded as
can be
expanded as
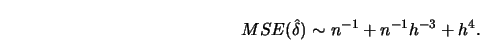 |
(10.4.12) |
A bandwidth minimizing this expression would therefore be proportional to
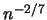 . Fourth, the determination of the cutoff sequence
. Fourth, the determination of the cutoff sequence 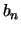 is somewhat
complicated in practice; it is therefore recommended to just cut off the lower
5 percent of the
is somewhat
complicated in practice; it is therefore recommended to just cut off the lower
5 percent of the  .
.
Let me come now to the estimation of 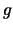 in 10.4.9. Assume
that in a first step
in 10.4.9. Assume
that in a first step
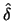 has been estimated, yielding the one-dimensional projection
has been estimated, yielding the one-dimensional projection
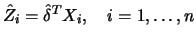 . Let
. Let
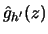 denote a
kernel estimator with one-dimensional kernel
denote a
kernel estimator with one-dimensional kernel 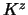 of the regression of
of the regression of 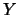 on
on 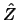 , that is,
, that is,
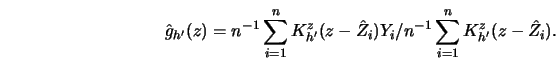 |
(10.4.13) |
Suppose, for the moment, that
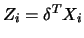 instead of
instead of 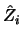 were used in 10.4.13. In this case, it is well known (Section
4.2) that
the resulting regression estimator is asymptotically normal
and converges at the optimal pointwise rate
were used in 10.4.13. In this case, it is well known (Section
4.2) that
the resulting regression estimator is asymptotically normal
and converges at the optimal pointwise rate 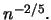 Theorem 10.4.2 states that there is
no cost in using the estimated projections
Theorem 10.4.2 states that there is
no cost in using the estimated projections 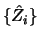 ,
that is, one achieves through additivity a dimension reduction, as considered
by Stone (1985).
,
that is, one achieves through additivity a dimension reduction, as considered
by Stone (1985).
Theorem 10.4.2
If the bandwidth
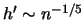
then
has a limiting normal distribution with mean
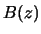
and variance
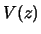
, where, with the density
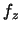
of
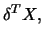
More formally, the ADE procedure is described in
Algorithm 10.4.1
STEP 1.
Compute 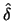 by 10.4.11 with
a cutt of
by 10.4.11 with
a cutt of 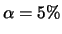 .
.
STEP 2.
Compute 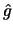 by 10.4.13 from
by 10.4.13 from
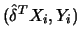 with
a one-dimensional cross-validated bandwith.
with
a one-dimensional cross-validated bandwith.
STEP 3.
Compose both steps into the function
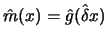 .
.
An application of this technique is given in Appendix 2 where I consider a
desirable computing environment for high dimensional smoothing techniques.
Simulations from the ADE algorithm for different nonparametric models in
more than four dimensions can be found in Härdle and Stoker (1989).
One model in this article is
where
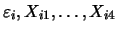 are independent standard
normally distributed random variables.
are independent standard
normally distributed random variables.
Table 10.1:
ADE estimation of the Sine model
| |
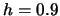 |
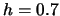 |
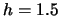 |
known density |
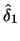 |
0.1134 |
0.0428 |
0.1921 |
0.1329 |
| |
(0.0960) |
(0.0772) |
(0.1350) |
(0.1228) |
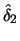 |
0.1356 |
0.0449 |
0.1982 |
0.1340 |
| |
(0.1093) |
(0.0640) |
(0.1283) |
(0.1192) |
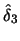 |
0.1154 |
0.0529 |
0.1837 |
0.1330 |
| |
(0.1008) |
(0.0841) |
(0.1169) |
(0.1145) |
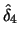 |
0.1303 |
0.0591 |
0.2042 |
0.1324 |
| |
(0.0972) |
(0.0957) |
(0.1098) |
(0.1251) |
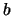 |
0.0117 |
0.0321 |
0.0017 |
|
Note: In brackets are
standard deviations over the Monte Carlo simulations.
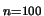 ,
,
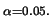
The average derivative takes the form
and some tedious algebra gives
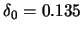 .
Table 10.1 reports the result over 100 Monte Carlo simulations with a
cutoff rule of
.
Table 10.1 reports the result over 100 Monte Carlo simulations with a
cutoff rule of 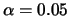 . It is remarkable that even in the case of a
known density (therefore,
. It is remarkable that even in the case of a
known density (therefore, 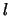 is known) the standard deviations (given in
brackets) are of similar magnitude to those in the case of unknown
is known) the standard deviations (given in
brackets) are of similar magnitude to those in the case of unknown 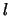 . This
once again demonstrates that there is no cost (parametric rate!)
in not knowing
. This
once again demonstrates that there is no cost (parametric rate!)
in not knowing 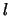 .
An actual computation
with
.
An actual computation
with 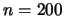 resulted in the values of
resulted in the values of
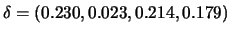 . The correlation
between
. The correlation
between
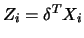 and
and
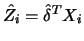 was
0.903. The estimated function
was
0.903. The estimated function
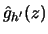 is
shown in Figure 10.13 together with the points
is
shown in Figure 10.13 together with the points
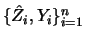 . A kernel smooth based on the true projections
. A kernel smooth based on the true projections
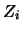 is depicted together with the smooth
is depicted together with the smooth
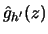 in Figure
10.14. The estimated
in Figure
10.14. The estimated
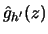 is remarkably close to the
true regression function as Figure 10.15 suggests.
is remarkably close to the
true regression function as Figure 10.15 suggests.
Figure:
The estimated curve
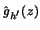 together with the projected data
together with the projected data
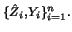
|
|
Figure 10.15:
The ADE smooth and the true curve.
The thin line indicates the
ADE smooth as in Figure 10.14 and Figure 10.13;
the thick line is the true curve
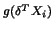 .
.
|
|
Exercises
10.4.1Prove formula 10.4.10.
10.4.2Explain the bandwidth condition ``that 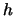 has to tend zero faster than the
optimal rate" from formula 10.4.12.
has to tend zero faster than the
optimal rate" from formula 10.4.12.
10.4.3Assume a partial linear model as in Chapter 8. How can you estimate the
parametric part by ADE?
10.4.4Assume  to be standard normal. What is
to be standard normal. What is 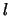 in this case?
in this case?
10.4.5In the case of a pure linear model 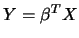 what is
what is 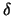 ?
?
![\begin{displaymath}\delta = E[ m'(X)]\end{displaymath}](anrhtmlimg2745.gif)
![\begin{displaymath}\delta = E[ m'(X)]\end{displaymath}](anrhtmlimg2745.gif)
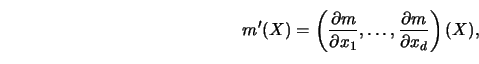
![]() is proportional to
is proportional to ![]() since
since
![\begin{displaymath}\delta = E[ m'(X)] = E [ dg/d(x^T\beta) ] \beta.\end{displaymath}](anrhtmlimg2749.gif)
![]() is
normalized in such a way that
is
normalized in such a way that
![]() Average derivative estimation(ADE) yields a
direct estimator for the weights
Average derivative estimation(ADE) yields a
direct estimator for the weights ![]() in 10.4.9.
(Note that as in PPR the model 10.4.9 is not identifiable unless we make
such a normalization assumption.)
in 10.4.9.
(Note that as in PPR the model 10.4.9 is not identifiable unless we make
such a normalization assumption.)
![]() denote the marginal density,
denote the marginal density,



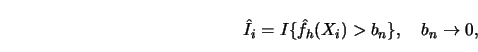
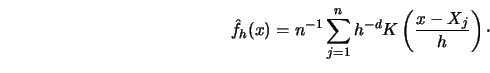

![\begin{displaymath}l(X)Y + [ m'(X) -l(X)m(X)]\ .\end{displaymath}](anrhtmlimg2765.gif)
![]() ; see Section 4.1.
The bandwidth
; see Section 4.1.
The bandwidth ![]() has to tend to zero
faster than the optimal rate in order to keep the bias of
has to tend to zero
faster than the optimal rate in order to keep the bias of
![]() below the desired
below the desired ![]() rate. A similar
observation has been made in the context of semiparametric models;
see Section 8.1. Second, the covariance matrix is constructed from
two terms,
rate. A similar
observation has been made in the context of semiparametric models;
see Section 8.1. Second, the covariance matrix is constructed from
two terms, ![]() and
and
![]() . If one knew the
marginal density then the first term
. If one knew the
marginal density then the first term ![]() would
determine the covariance. It is the estimation of
would
determine the covariance. It is the estimation of
![]() by
by ![]() that brings in this second term. Third, the
bandwidth condition is of qualitative nature, that is, it says that
that brings in this second term. Third, the
bandwidth condition is of qualitative nature, that is, it says that ![]() should
tend to zero not ``too fast" and not ``too slow."
A more refined analysis
(Härdle, Hart, Marron and Tsybakov 1989) of
second-order terms shows that for
should
tend to zero not ``too fast" and not ``too slow."
A more refined analysis
(Härdle, Hart, Marron and Tsybakov 1989) of
second-order terms shows that for ![]() the MSE of
the MSE of ![]() can be
expanded as
can be
expanded as
![]() in 10.4.9. Assume
that in a first step
in 10.4.9. Assume
that in a first step
![]() has been estimated, yielding the one-dimensional projection
has been estimated, yielding the one-dimensional projection
![]() . Let
. Let
![]() denote a
kernel estimator with one-dimensional kernel
denote a
kernel estimator with one-dimensional kernel ![]() of the regression of
of the regression of ![]() on
on ![]() , that is,
, that is,
![\begin{displaymath}n^{2/5} [ \hat g_{h'}(z)- g(z)] \end{displaymath}](anrhtmlimg2785.gif)
![\begin{eqnarray*}
B(z) &=&{1\over 2}[ g''(z)+ g'(z)f_z'(z)/f_z(z) ] d_{K^z}, \cr
V(z) &=&\textrm{var}[ Y \vert \delta^T X=z ] c_{K^z}. \end{eqnarray*}](anrhtmlimg2790.gif)
![]() by 10.4.11 with
a cutt of
by 10.4.11 with
a cutt of ![]() .
.
![]() by 10.4.13 from
by 10.4.13 from
![]() with
a one-dimensional cross-validated bandwith.
with
a one-dimensional cross-validated bandwith.
![]() .
.
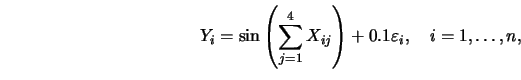

![\includegraphics[scale=0.15]{ANR10,14.ps}](anrhtmlimg2817.gif)
![\includegraphics[scale=0.15]{ANR10,15.ps}](anrhtmlimg2819.gif)
![]() has to tend zero faster than the
optimal rate" from formula 10.4.12.
has to tend zero faster than the
optimal rate" from formula 10.4.12.
![]() to be standard normal. What is
to be standard normal. What is ![]() in this case?
in this case?
![]() what is
what is ![]() ?
?