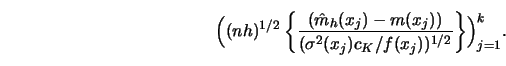The aim of this section is to develop the construction of pointwise confidence
intervals for kernel estimators and to prepare the ground for the uniform
confidence bands which are treated in the next section. The basic idea is to
derive the asymptotic distribution of the kernel smoothers and then to use
either asymptotic quantiles or bootstrap approximations for these quantiles
for the confidence intervals. The shrinkage rate of the confidence intervals
is proportional to ![]() , the optimal rate of convergence if the bandwidth
is chosen so that the optimal rate is achieved. It is certainly desirable to
use smoothers that are asymptotically optimal since they give the narrowest
confidence intervals obtainable and keep the squared bias and variance at the
same order.
, the optimal rate of convergence if the bandwidth
is chosen so that the optimal rate is achieved. It is certainly desirable to
use smoothers that are asymptotically optimal since they give the narrowest
confidence intervals obtainable and keep the squared bias and variance at the
same order.
The reader more interested in practical aspects should not be discouraged by
the rather theoretical beginning of this section, but instead should jump to
Algorithm 4.2.1, which describes the construction of confidence intervals at
![]() different points.
different points.
The asymptotic distribution is normal. The center of this distribution is
shifted by the asymptotic bias which depends on derivatives of the regression
curve and the marginal density of ![]() . The asymptotic variance is a function
of
. The asymptotic variance is a function
of
the conditional variance ![]()
the kernel ![]() ; and
; and
the marginal density ![]() .
.
The asymptotic bias is a function of
the kernel ![]() ; and
; and
derivatives of ![]() and
and ![]() .
.
Before I come to the theoretical statement of the asymptotic distribution of
kernel smoothers let me point out some simplifications. The kernel smoother
![]() is a ratio of random variables, direct central limit theorems
therefore cannot be applied and the smoother has to be linearized. The kernel
estimator has the same limit distribution as the right-hand side of the
following linearization,
is a ratio of random variables, direct central limit theorems
therefore cannot be applied and the smoother has to be linearized. The kernel
estimator has the same limit distribution as the right-hand side of the
following linearization,
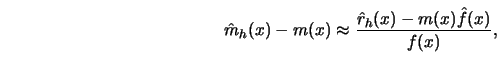
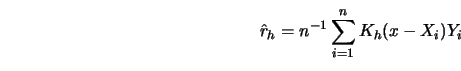
30pt
to 30pt(A1)
![]() for some
for some
![]()
30pt
to 30pt(A2)
![]()
30pt
to 30pt(A3)![]() and
and ![]() are twice differentiable;
are twice differentiable;
30pt
to 30pt(A4)the distinct points
![]() are continuity
points of
are continuity
points of ![]() and
and
![]() and
and
![]() .
.
Then the suitably normalized Nadaraya-Watson kernel smoother
![]() at
the
at
the ![]() different locations
different locations
![]() converges in distribution to a
multivariate normal random vector with mean vector
converges in distribution to a
multivariate normal random vector with mean vector ![]() and identity covariance
matrix,
and identity covariance
matrix,
The proof is given in the Complements extending results of Johnston (1979) and of Schuster (1972). The proof is based on the linearization given above.
The asymptotic bias 4.2.8 is proportional to the second moment of the kernel
and a measure of local curvature of ![]() . This measure of local curvature is
not a function of
. This measure of local curvature is
not a function of ![]() alone but also of the marginal density. At maxima or
minima, the bias is a multiple of
alone but also of the marginal density. At maxima or
minima, the bias is a multiple of ![]() alone; at deflection points it is
just a multiple of only
alone; at deflection points it is
just a multiple of only
![]() .
.
This theorem can be used to define confidence intervals. Suppose that the bias is of negligible magnitude compared to the variance, then the following algorithm yields approximate confidence intervals.
Compute the kernel smoother ![]() and the density estimate
and the density estimate ![]() at
distinct points
at
distinct points
![]() .
.
STEP 2.
Construct an estimate of ![]() ,
,
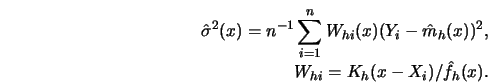
STEP 3.
Take ![]() , the
, the ![]() -quantile of the normal distribution, and
let
-quantile of the normal distribution, and
let
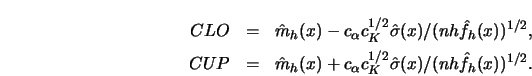
STEP 4.
Draw the interval
![]() around
around
![]() at the
at the ![]() distinct
points
distinct
points
![]() .
.
pt
This algorithm does not take the bias of
![]() into account, since the
bias is a complicated function of
into account, since the
bias is a complicated function of ![]() and
and ![]() . Bias estimates could be built
in by using estimates of the derivatives of
. Bias estimates could be built
in by using estimates of the derivatives of ![]() and
and ![]() but would considerably
complicate the algorithm. So if the bandwidth
but would considerably
complicate the algorithm. So if the bandwidth
![]() then the above
steps do not lead asymptotically to an exact confidence interval. However, if
then the above
steps do not lead asymptotically to an exact confidence interval. However, if
![]() is chosen proportional to
is chosen proportional to ![]() times a sequence that tends slowly to
zero, then the bias vanishes asymptotically.
times a sequence that tends slowly to
zero, then the bias vanishes asymptotically.
If the variation in ![]() and
and ![]() is moderate, little difference is to be
expected between such two sequences of bandwidths, so one could use the
unshifted confidence intervals as well. However, at small peaks (high bias!)
it may be desirable to shift the
is moderate, little difference is to be
expected between such two sequences of bandwidths, so one could use the
unshifted confidence intervals as well. However, at small peaks (high bias!)
it may be desirable to shift the
![]() interval by a bias
estimate. The decision of the occurrence of such peaks has to be made by the
statistician. The analysis of expenditure data is a field where we do not
expect sudden and abrupt changes of
interval by a bias
estimate. The decision of the occurrence of such peaks has to be made by the
statistician. The analysis of expenditure data is a field where we do not
expect sudden and abrupt changes of ![]() . In Figure 4.1 an estimate of the
regression curve for the potato versus net income example (Figure
1.1) is
shown together with ten pointwise confidence intervals.
. In Figure 4.1 an estimate of the
regression curve for the potato versus net income example (Figure
1.1) is
shown together with ten pointwise confidence intervals.
![\includegraphics[scale=0.7]{ANRpotconf.ps}](anrhtmlimg1018.gif)
|
It is apparent from this picture that the confidence interval lengths increase
as they move to the right boundary of the observation interval. Since the
kernel is a fixed function, this must be due to the other factors controlling
the variance of the kernel smoother. First, it is the conditional variance
![]() which increases as
which increases as ![]() goes to the right boundary (compare with
Figure 1.1).
Secondly, the inverse of the marginal
goes to the right boundary (compare with
Figure 1.1).
Secondly, the inverse of the marginal ![]() -distribution enters
as a proportionality factor. Since the data are more sparse near the right
boundary, (compare with Figure 1.5), the variance estimate also gets
inflated for this reason. A plot of
-distribution enters
as a proportionality factor. Since the data are more sparse near the right
boundary, (compare with Figure 1.5), the variance estimate also gets
inflated for this reason. A plot of
![]() , an estimate of the
conditional standard deviation curve,
, an estimate of the
conditional standard deviation curve, ![]() is presented in Figure
4.2.
is presented in Figure
4.2.
![\includegraphics[scale=0.7]{ANRpotdev.ps}](anrhtmlimg1022.gif)
|
As a possible way of visualizing both effects in one plot, I propose plotting
confidence intervals at points ![]() such that the number of observations
between
such that the number of observations
between ![]() and
and ![]() is constant. As the marginal density decreases,
the Euclidean distance between neighboring points
is constant. As the marginal density decreases,
the Euclidean distance between neighboring points ![]() will become bigger.
This can be seen from Figure 4.3, which shows a kernel smooth (
will become bigger.
This can be seen from Figure 4.3, which shows a kernel smooth (![]() ,
Epanechnikov kernel) of the potato versus net income data together with
confidence intervals. These intervals are placed such that in between
successive intervals there are a fixed number of 700 data points.
,
Epanechnikov kernel) of the potato versus net income data together with
confidence intervals. These intervals are placed such that in between
successive intervals there are a fixed number of 700 data points.
![\includegraphics[scale=0.7]{ANRpotconf2.ps}](anrhtmlimg1025.gif)
|
There are always 700 observations between neighboring gridpoints ![]() . In
this plot, one not only sees an increase of the variance but also a decrease
of the marginal density
. In
this plot, one not only sees an increase of the variance but also a decrease
of the marginal density ![]() . This becomes apparent at the right boundary:
The peak to the right of the approximate confidence interval at
. This becomes apparent at the right boundary:
The peak to the right of the approximate confidence interval at
![]() is produced by less than fifty observations.
is produced by less than fifty observations.
Another method of constructing confidence bands is based on the bootstrap. The
bootstrap is a resampling technique that prescribes taking ``bootstrap
samples'' using the same random mechanism that generated the data. This
prescription makes it necessary to handle the case of stochastic ![]() s
differently from the case of deterministic
s
differently from the case of deterministic ![]() -values. To be precise, in the
fixed design model the stochastic part of the data is contained only in the
observation errors, so resampling should take place from residuals. If both
-values. To be precise, in the
fixed design model the stochastic part of the data is contained only in the
observation errors, so resampling should take place from residuals. If both
![]() and
and ![]() are random, resampling can be done from the data pairs
are random, resampling can be done from the data pairs
![]() according to the following algorithm.
according to the following algorithm.
REPEAT
b=b+1
STEP 1.
Sample
![]() from the empirical distribution function
of the data.
from the empirical distribution function
of the data.
STEP 2.
Construct the kernel smoother
![]() from the bootstrap sample
from the bootstrap sample
![]() .
.
UNTIL b=B=number of bootstrap samples.
STEP 3.
Define ![]() as the
as the ![]() empirical quantile of the
empirical quantile of the ![]() bootstrap
estimates
bootstrap
estimates
![]() . Define
. Define ![]() analogously.
analogously.
STEP 4.
Draw the interval
![]() around
around
![]() at the
at the ![]() -distinct points
-distinct points
![]() .
.
This bootstrap algorithm was proposed by McDonald (1982) in his Orion
workstation film. Theoretical properties of this so-called naive
bootstrap have been considered by Dikta (1988), again by disregarding bias
terms. The above bootstrap procedure was applied with ![]() to the simulated
data set of Table 3.2. The result is depicted in Figure
4.4.
to the simulated
data set of Table 3.2. The result is depicted in Figure
4.4.
![\includegraphics[scale=0.7]{ANRsimboot.ps}](anrhtmlimg1034.gif)
|
The kernel smooth for Figure 4.4 was computed with the Epanechnikov kernel
(
![]() ) and bandwidth
) and bandwidth ![]() . Note
that this bandwidth is bigger than the one chosen to produce the kernel smooth
of Figure 3.21 but the curve from Figure 4.4 is smoother than that of
Figure 3.21. The reason for this is the use of different kernels. A possible
means of comparing these bandwidths is presented in Section
5.4.
. Note
that this bandwidth is bigger than the one chosen to produce the kernel smooth
of Figure 3.21 but the curve from Figure 4.4 is smoother than that of
Figure 3.21. The reason for this is the use of different kernels. A possible
means of comparing these bandwidths is presented in Section
5.4.
In the case of the fixed design models with homoscedastic error structure one
may use only the estimated residuals

This bootstrap from residuals can also be applied in the stochastic design
setting. It is then able also to incorporate the bias term and is called wild bootstrap by Härdle and Mammen (1988). It is called wild, since
at each observation point ![]() (in the fixed or stochastic design setting) a
bootstrap observation is drawn from one single estimated residual. This
is done to better retain the conditional distributional characteristics of the
estimate. It is not resampled from the entire set of residuals, as in Härdle
and Bowman (1988).
(in the fixed or stochastic design setting) a
bootstrap observation is drawn from one single estimated residual. This
is done to better retain the conditional distributional characteristics of the
estimate. It is not resampled from the entire set of residuals, as in Härdle
and Bowman (1988).
A different possibility would be to resample from a set of residuals determined by a window function, but this has the disadvantage of requiring choice of the window width. To avoid this I propose wild bootstrapping, where each bootstrap residual is drawn from the two-point distribution which has mean zero, variance equal to the square of the residual, and third moment equal to the cube of the residual.
In particular, let


Then the kernel smoother is applied to the bootstrapped data
![]() using bandwidth
using bandwidth ![]() . Let
. Let
![]() denote this kernel smooth.
A number of replications of
denote this kernel smooth.
A number of replications of
![]() can be used as the basis for a
confidence interval because the distribution of
can be used as the basis for a
confidence interval because the distribution of
![]() is
approximated by the distribution of
is
approximated by the distribution of
![]() , as Theorem
4.2.2
shows. Here the symbol
, as Theorem
4.2.2
shows. Here the symbol ![]() is used to denote the conditional
distribution of
is used to denote the conditional
distribution of ![]() , ...,
, ..., ![]() , ...,
, ..., ![]() , and the symbol
, and the symbol ![]() is used to denote the bootstrap distribution of
is used to denote the bootstrap distribution of ![]() , ...,
, ...,
![]() , ...,
, ..., ![]() .
.
For an intuitive understanding of why the bandwidth
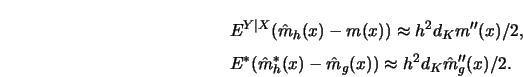
REPEAT
b=b+1
STEP 1.
Sample ![]() from the two-point distribution
from the two-point distribution ![]() 4.2.9, where
4.2.9, where


Construct new observations

UNTIL b=B=number of bootstrap samples.
STEP 3.
Define ![]() as the
as the ![]() empirical quantile of the B bootstrap
estimates
empirical quantile of the B bootstrap
estimates
![]() . Define
. Define ![]() analogously.
analogously.
STEP 4.
Draw the interval
![]() around
around
![]() at the
at the
![]() -distinct points
-distinct points
![]() .
.
Exercises
4.2.1 Show that the difference between


[Hint: Write the difference as

4.2.2 Prove formula 4.2.8, that is, show that
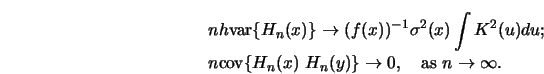
4.2.3 Write an efficient program for wild bootstrapping using the WARPing technique as described in Section 3.1.
4.2.4 Use the wild bootstrap confidence intervals in a real example. Compare them with the asymptotic confidence intervals from Theorem 4.2.1.
4.2.5 Ricardo Cao has found that the wild bootstrap is related to the
Golden Section method of Euclid (-300). Show that the two-point distribution
of the wild bootstrap can be found by using the outer Golden Section of the
interval
![]() .
.
[Hint: The outer Golden Section ![]() is that interval
containing
is that interval
containing ![]() such that the ratio of the length of
such that the ratio of the length of ![]() to the length of
to the length of ![]() is the same as the ratio of the length of
is the same as the ratio of the length of ![]() to that of
to that of ![]() .]
.]
Define
![]() .
The difference between
.
The difference between


The bias can then be written as



Note that
![\begin{displaymath}{\hat{m}}_h-m_n=[ {\hat{r}}_h/f-({\hat{f}}_h/f) m_n ] (f/{\hat{f}}_h)\end{displaymath}](anrhtmlimg1096.gif)