
Observe that if one used a kernel of the form

More generally, consider the situation in which two statisticians analyze the same data set but use different kernels for their smoothers. They come up with some bandwidths that they like. Their smoothing parameters have been determined subjectively or automatically, but they have been computed for different kernels and therefore cannot be compared directly. In order to allow some comparison one needs a common scale for both bandwidths. How can we find such a ``common scale?"
A desirable property of such a scale should be that
two kernel smoothers with the same bandwidth should ascribe
the same amount of smoothing to the data.
An approach to finding a representative member of each equivalence class of
kernels has already been presented in Section 4.5. Epanechnikov (1969) has
selected kernels with kernel constant ![]() . Another approach taken by Gasser,
Müller and Mammitzsch (1985) insists that the support of the kernel be
. Another approach taken by Gasser,
Müller and Mammitzsch (1985) insists that the support of the kernel be
![]() . A drawback to both methods is that they are rather arbitrary and
are not making the attempt to give the same amount of smoothing
for different kernels.
. A drawback to both methods is that they are rather arbitrary and
are not making the attempt to give the same amount of smoothing
for different kernels.
An attempt for such a joint scale is given by so-called
canonical kernels in the class of kernels ![]() (Marron and Nolan 1988). It is based on the well-known expansion of the MSE
for
(Marron and Nolan 1988). It is based on the well-known expansion of the MSE
for ![]() and
and ![]() ,
,
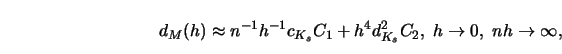

![\begin{displaymath}s=s^*= \left[ {c_K \over d_K^2} \right]^{1/5}\end{displaymath}](anrhtmlimg1785.gif)
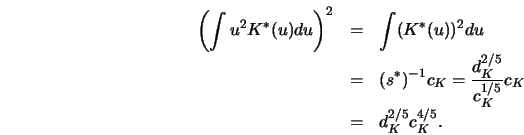
![\begin{displaymath}d_M (h) \approx (d_K)^{2/5} (c_K)^{4/5} [ n^{-1} h^{-1}
C_1 + h^4 C_2 ],\end{displaymath}](anrhtmlimg1788.gif)
The advantage of canonical kernels is that they allow simple comparison
between different kernel classes. Suppose that ![]() and
and ![]() are the canonical kernels from each class and that
one wants the two estimated
curves to represent the same amount of smoothing, that is, the variance and
bias
are the canonical kernels from each class and that
one wants the two estimated
curves to represent the same amount of smoothing, that is, the variance and
bias![]() trade-off should be the same for both smoothers.
This is simply achieved by using the same bandwidth for both estimators.
If canonical kernels are used, the
trade-off should be the same for both smoothers.
This is simply achieved by using the same bandwidth for both estimators.
If canonical kernels are used, the ![]() functions will look
different for the two kernels, as one is a multiple of the other, but
each
will have its minimum at the same place. The kernel class that has the
lowest minimum is given by the ``optimal kernel" of order 2, the
so-called Epanechnikov kernel.
functions will look
different for the two kernels, as one is a multiple of the other, but
each
will have its minimum at the same place. The kernel class that has the
lowest minimum is given by the ``optimal kernel" of order 2, the
so-called Epanechnikov kernel.
One interesting family of kernels, which contains many of the kernels used in
practice, is
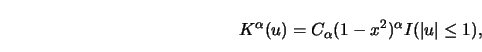
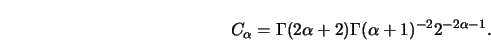
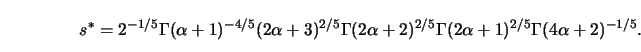
| Kernel | |||||
| Uniform | 0 | ||||
| Epanechnikov | 1 | ||||
| Quartic | 2 | ||||
| Triweight | 3 |
|
|||
| Gaussian | - |
|
In practice, one uses kernels that are not necessarily canonical, since
one is used to thinking in terms of a certain scale of the kernel, for example,
multiples of the standard deviation for the normal kernel. How does one
then compare the smoothing parameters ![]() between laboratories? The following
procedure is based on canonical kernels. First transform the scale of
both kernel classes to the canonical kernel
between laboratories? The following
procedure is based on canonical kernels. First transform the scale of
both kernel classes to the canonical kernel
![]() .
Then compare the bandwidths for the respective canonical kernels.
More formally, this procedure is described in Algorithm 5.4.1.
.
Then compare the bandwidths for the respective canonical kernels.
More formally, this procedure is described in Algorithm 5.4.1.
Algorithm 5.4.1
Suppose that lab ![]() used kernel
used kernel ![]() and bandwidth
and bandwidth ![]() .
.
STEP 1.
Transform ![]() to canonical scale:
to canonical scale:

Decide from the relation of
![]() to
to
![]() whether both labs have produced the same smooth or whether one or the other
has over- or undersmooothed.
whether both labs have produced the same smooth or whether one or the other
has over- or undersmooothed.
Suppose, for example, that laboratory 1 used the Gaussian kernel and
came up with a bandwidth of, say, ![]() (see Figure 3.21). Another
statistician in laboratory 2 used a quartic kernel and computed
from cross-validation a bandwidth of
(see Figure 3.21). Another
statistician in laboratory 2 used a quartic kernel and computed
from cross-validation a bandwidth of ![]() (see Figure
5.4). A
typical situation is depicted in Figure 5.19, showing the average
squared error
(see Figure
5.4). A
typical situation is depicted in Figure 5.19, showing the average
squared error
![]() for the Gaussian and the quartic kernel smoothers as applied to
the simulated data set from Table 2 in the Appendix. Obviously, the
bandwidth minimizing each of these functions gives the same amount of
trade-off between bias
for the Gaussian and the quartic kernel smoothers as applied to
the simulated data set from Table 2 in the Appendix. Obviously, the
bandwidth minimizing each of these functions gives the same amount of
trade-off between bias![]() and variance.
and variance.
![\includegraphics[scale=0.7]{ANRsimase.ps}](anrhtmlimg1825.gif)
|
Let me compute ![]() explicitly for this example.
The factor
explicitly for this example.
The factor ![]() for the Gaussian kernel is
for the Gaussian kernel is
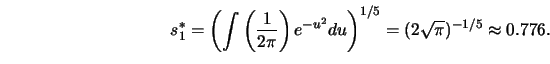
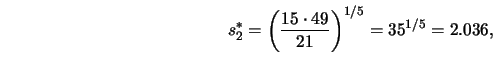
In summary, the optimal bandwidth
![]() is 0.0736
(on the canonical kernel scale), which means that my subjective choice
(Figure 3.21) for this simulated example of
is 0.0736
(on the canonical kernel scale), which means that my subjective choice
(Figure 3.21) for this simulated example of ![]() resulted
in slight undersmoothing.
resulted
in slight undersmoothing.
Exercises
5.4.1Compute the canonical kernel from the triangular kernel.
5.4.2Derive the canonical kernels for the derivative kernels from Section 4.5.
5.4.3Try kernel smoothing in practice and transform your bandwidth by the procedure of Algorithm 5.4.1. Compare with another kernel smooth and compute the bandwidth that gives the same amount of smoothing for both situations.