3.11 A comparison of kernel, k-NN and spline smoothers

The purpose of this section is to present a comparative study of the three most commonly used and easy-to-implement smoothers: the kernel, the $k$-nearest neighbor and the cubic spline smoothers. The comparison is performed theoretically and empirically. The practical comparison is based on a simulated data set, which is presented in Table 2 in Appendix 2.

The theoretical comparison is presented for the two design models - fixed equidistant and random design. Kernel estimators $\hat m_h$ with weight functions $\{ W_{hi}^{(3)}\}$ and $\{ W_{hi} \}$ (see Section 3.1) and the $k$-$NN$ smoother $\hat m_R$ are compared. Although the spline estimator also makes sense for stochastic predictor variables its statistical properties have been studied mostly for the fixed design case. We have found in Section 3.6 that the fixed design spline almost acts like a kernel smoother with design dependent bandwidth. Recall the kernel-spline equivalence theorem, Theorem 3.6.1 It says that the spline estimator $\hat m_\lambda$ for regularly distributed $X_i = F^{-1}((i-1/2)/n)$ behaves like a Priestley-Chao kernel smoother with effective local bandwidth

$$h(x) = \lambda^{1/4} f(x)^{1/4}.$$

The effective local bandwidth is thus a power of the density of the $X$ variables, $f^\alpha(x)$.

From Table 3.1 we saw that the $k$-$NN$ estimator $\hat m_R$ has mean squared error properties comparable to the kernel estimator if the bandwidth $R(x) \sim f(x)^{-1}.$ It therefore makes sense to consider kernel smoothers with bandwidths proportional to $f(x)^{- \alpha}, \ \alpha \in [0,1].$

Bias and variance behaviors of kernel smoothers with weigths $\{ W_{hi}^{(3)}\}$ and bandwidth $h \sim f^\alpha$ have been studied by Jennen-Steinmetz and Gasser (1988). The bias and variance of the above three estimators for the fixed equidistant design $(d=1, X_i = i/n, \alpha = 0 )$ are listed in Table 3.2. For the correct interpretation of this table recall the definition of $c_K, d_K$ as given in Section 3.1. Table 3.2 shows clearly that the two kernel sequences $\{ W_{hi}^{(3)}\}$ and $\{ W_{hi} \}$ have the same mean squared error properties for the fixed equidistant design case. As noted before the $k$-$NN$ weight sequence can be seen as a kernel sequence if we make the identification $h = { k \over 2n}$.

Table 3.2: Pointwise bias and variance of k-NN and kernel smoothers for the fixed design case

	bias	variance
kernel weights $\{ W_{hi} \}$	$h^2 \frac{m''(x)}{2} d_K$	$\frac{\sigma^2(x)}{nh}c_K$
kernel weights $\{ W_{hi}^{(3)}\}$	$h^2 \frac{m''(x)}{2} d_K$	$\frac{\sigma^2(x)}{nh}c_K$
k-NN weights	$(\frac{k}{n})^2\frac{m''(x)}{8}d_K$	$\frac{2\sigma^2(x)}{k}c_K$

Source: Jennen-Steinmetz and Gasser (1988, table 1).

The bias and variance for the random design case is drastically different, as Table 3.3 shows. Pointwise bias and variance are complicated functionals not only of the regression curve $m$ but also of the marginal density $f$.

Pointwise bias and variance of k-NN and kernel smoothers for the random design case

Table 3.3:

	bias	variance
kernel weights $\{ W_{hi} \}$	$h^2\frac{(m''f+2m'f')(x)}{2f(x)}d_K$	$\frac{\sigma^2(x)}{nhf(x)}c_K$
kernel weights $\{ W_{hi}^{(3)}\}$	$h^2\frac{m''(x)}{2f(x)^{2\alpha}}d_K$	$\frac{2\sigma^2(x)}{nhf(x)^{1-\alpha}}c_K$
k-NN weights	$(\frac{k}{n})^2\frac{(m''f+2m'f')(x)}{8f^3(x)}d_K$	$\frac{2\sigma^2(x)}{k}c_K$

Source: Jennen-Steinmetz and Gasser (1988, table 1).

Note that essentially all three estimators coincide for the fixed design case when chosing $k=2nh$ as indicated already in Section 3.4. This is not true for the random design. For $\alpha=0$ the variance of the kernel with weights $\{ W_{hi}^{(3)}\}$ is twice as big as for the Nadaraya-Watson estimator. By constrast, the bias of the Nadaraya-Watson smoother is a complicated expression of $m$ and $f$. The same is true when comparing the bias of the $k$-$NN$ smoother for $\alpha =1$.

The empirical study is based on the simulated data from Figure 3.20. It shows $n = 100$ data points simulated from the regression curve

$$m(x)=1-x+e^{-200\ (x-1/2)^2}.$$

The $X$-variate is uniformly stochastically distributed over the unit interval and the observation errors $\varepsilon_i$ have standard normal distributions. (Pseudo-random number generators based on Marsaglia's shuffling method for uniforms and the polar-Marsaglia method for normals were used for this plot; see Morgan 1984.)

Figure 3.20: A simulated data set. The raw data $\{ (X_i,Y_i) \}^n_{i=1}$, $n=100$ were constructed from $Y_i = m(X_i) + \varepsilon _i, \varepsilon _i \sim N(0,1), X_i \sim U(0,1)$ and $m(x) = 1-x+e^{-200\ (x-1/2)^2}$. ANRsimul.xpl

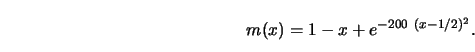
A list of the values $\{(X_i, Y_i) \}^n_{i=1}$ is given in Table 2 in Appendix 2. After looking at Figure 3.20 one might say that this example is somewhat extreme since most of ``the signal seems to be buried in the noise." By contrast, I consider it as realistic since it shows what can happen in practice. The sunflower plot of the food versus net income example in Chapter 2 gave an impression of such a ``realistic data set." Note that the pattern of observation errors in the region around $x \approx 0.25$ seems to be skewed toward positive errors. Any smoother must therefore have a tendency to lie slightly above the true regression curve in this region. This can be seen immediately from the plot of the kernel smoother (Figure 3.21).

Figure 3.21: A kernel smooth of the simulated data set. The solid line (label 1) denotes the underlying regression curve $m(x) = 1-x+e^{-200\ (x-1/2)^2}$. The dashed line (label 2) is the kernel smooth $\hat m_h(x)$, $h= 0.05$, Gaussian kernel $K(u) = \exp(-u^2/2)/(\sqrt{2 \pi})$ from the simulated data given in Table 2 in the Appendix. ANRsimkernel.xpl

The kernel weights

$$W_{hi}(x)=K_h(x-X_i)/ \hat f_h(x)$$

of the Nadaraya-Watson estimator have been used here with a Gaussian kernel $K(u)=(2 \pi)^{-1/2} \exp(-u^2/2)$ and bandwidth $h=0.05$. Note that this bandwidth does not mean that the observations are averaged in an interval of length 0.1. Rather, the kernel weights based on the above $K$ extend over the whole interval but downweight observations that are away from the center of the kernel. In this example, $\hat f_h \approx 1$ since the $X$-distribution is uniform. Observations near $x$ will receive weight 2.65 whereas an observation which is $2h$ away will be given weights 0.35.

Special attention must be paid to the boundary points 0 and 1 of the observation interval. Estimation points $x$ that are close to the boundary have only a one-sided neighborhood over which to average the $Y$-values. The kernel smoother must therefore be less accurate at the boundary (see Section 4.4 for a mathematical formulation of this problem). This inaccuracy can be seen from Figure 3.21 near the left boundary: most of the observations there lie below the true regression curve, the asymmetric average therefore considerably underestimates the true $m(x)$ near $x \approx 0$.

The bandwidth $h=0.05$ was chosen completely subjectively. I asked several colleagues and they felt that a higher amount of smoothing would ``wash out" too much structure and a smaller bandwidth would give too rough a curve. Had another kernel been used, for instance a kernel with compact support, the picture would have been different for this specific bandwidth of $h=0.05$. The reason is that different kernels are in general differently scaled. A way of adjusting the bandwidths and kernels to the same scale is discussed in Section 5.4.

The $k$-$NN$ estimate produced a slightly rougher curve. In Figure 3.22 the graph of the $k$-$NN$ smoother, as defined in (3.4.19), is displayed for $k=11.$ The reason for the ``wiggliness" is the so-called uniform weight sequence that is used in (3.4.19). Theoretically speaking, the $k$-$NN$ smooth is a discontinuous function.

Figure 3.22: A $k$- $NN$ smooth of the simulated data set (Table 3.2). The solid line (label 1) denotes the underlying regression curve $m(x) = 1-x+e^{-200\ (x-1/2)^2}$. The dashed line (label 2) is the $k$- $NN$ smooth $\hat m_k(x), k= 11$. Gaussian kernel $K(u) = \exp(-u^2/2)/(\sqrt{2 \pi})$ from the simulated data given in Table 2 in Appendix 2. ANRsimknn.xpl

In practice, this means that as the window of weights moves over the observation interval, new observations enter at the boundary of the ``uniform window" according to the nearest neighbor rule. Any entering observation that has a value different from the current average will cause an abrupt change of the $k$-$NN$ smoother. Such an effect would be diminished if a smoother $k$-$NN$ weight sequence, like the one defined in (3.4.19), were used.

Here also boundary effects need special discussion. As the estimation point $x$ moves to the boundary, the interval of observations entering the determination of the smoother becomes asymmetric. This was also the case for the kernel smoothers. Note, however, that, in contrast to kernel smoothing, the asymmetric region left or right of $x$ always has the same number of points. The averaging procedure near the boundary thus involves a lot more points which, in general, have different mean values. This is not so drastic in our example since the regression curve is relatively flat at the boundaries. In cases where the regression function is steeper at the boundary the $k$-$NN$ smoother is expected to be more biased than the kernel smoother.

The smoothing parameter $k$ was also chosen subjectively here. A bigger $k$ seemed to me to yield too smooth a curve compared to the raw observations. A smaller $k$ produced too rough a curve, and amplified local spiky structures such as the one at $X \approx 0.85$.

The spline smoother $\hat m_{\lambda }(x)$ is shown in Figure 3.23. The algorithm of Reinsch (1967) was used to generate the smooth $\hat m_{\lambda }$. The smoothing parameter was chosen to be $\Lambda = 75$; that is, $\hat m_{ \Lambda}$ is the solution to the minimization problem

$$\int [g''(x)]^2 dx = \min!$$

under the constraint

$$\sum^n_{i=1} (Y_i -g(X_i))^2 \le \Lambda.$$

The relation of $\Lambda$ to the smoothing parameter $\lambda$ was presented in Section 3.6.

In Table 3.4 the relation between $\Lambda$ and $G(\Lambda) = \int (\hat m_{\Lambda}''(x))^2 dx$ is shown. As $\Lambda$ increases the spline curve becomes flatter and flatter. In the limit it is equivalent to fitting a least squares line.

Figure 3.23: A spline smooth of the simulated data set (Table 3.2). The solid line (label 1) denotes the underlying regression curve $m(x) = 1-x+e^{-200\ (x-1/2)^2}$. The dashed line (label 2) is the spline smooth $\hat m_\Lambda(x)$, $\Lambda= 75$, computed with the IMSL routine ICSSCU. ANRsimspline.xpl

Table 3.5 presents the equivalent parameter $\Lambda$ for various values of $\lambda.$ The $\lambda$ equivalent to $\Lambda = 75$ is therefore $\lambda=0.6 \times 10^{-5}$.

Table: The function $G(\Lambda) = \int (\hat m_{\Lambda}''(x))^2 dx$ as a function of $\Lambda$.

$\Lambda$	$G(\Lambda) = \int (\hat m_{\Lambda}''(x))^2 dx$
$45$	$0.18\times10^9$
$50$	$0.72\times10^8$
$55$	$0.29\times10^8$
$60$	$0.11\times10^8$
$65$	$0.36\times10^7$
$70$	$0.10\times10^7$
$75$	$0.21\times10^6$
$80$	$0.24\times10^5$
$85$	$0.35\times10^4$
$90$	$0.38\times10^3$
$95$	$0.23\times10^2$
$100$	$0.23\times10^1$
$105$	$0.68\times10^{-26}$

Table 3.5: The parmater $\lambda$ as a function of $\Lambda$.

$\Lambda$	$-1/G'(\Lambda)$
$50$	$0.47 \times 10^{-7}$
$55$	$0.12 \times 10^{-6}$
$60$	$0.28 \times 10^{-6}$
$65$	$0.70 \times 10^{-6}$
$70$	$0.20 \times 10^{-5}$
$75$	$0.61 \times 10^{-5}$
$80$	$0.27 \times 10^{-4}$
$85$	$0.24 \times 10^{-3}$
$90$	$0.16 \times 10^{-2}$
$95$	$0.14 \times 10^{-1}$
$100$	$0.24$
$105$	$0.22 \times 10^1$

By construction, the spline fit looks very smooth since it is a function that is glued together from pieces of cubic polynomials. The overall shape of the spline function is the same that as for the kernel and $k$-$NN$ smooth. The peak in the middle of the observation interval is relatively well approximated (Figure 3.24), but to the left of it all smoothers exhibit a somewhat smaller bump that is really only a random function of the data pattern.

Note that the spline smoother may produce a partially negative smooth even when all the response variables are positive. This can be understood from the asymptotic kernel representation (3.6.35) of $\hat m_{\lambda }$. Since the kernel $K_s$ has negative side lobes (Figure 3.10) it may happen that for a sparse data pattern the resulting spline smooth is negative although one averages over purely positive observations.

A comparison of the behavior of all three smoothers can be obtained from Figure 3.24, the residual curves (``fit" minus ``true") for the three approximation methods. All three smoothers have the artificial bump at $x \approx 0.2$, introduced by the data pattern, but show essentially the same behavior in the residual curves.

Figure 3.24: Residual plot of $k$- $NN$, kernel and spline smoother for the simulated data set (Table 3.2). The fine dashed line (label 1) denotes the $k$- $NN$ residual, $\hat m_k(x) - m(x), k=11$. The dashed line (label 2) is the spline residual with $\hat m_\Lambda(x) - m(x), \Lambda = 75$. The solid line (label 3) is the kernel residual $\hat m_h(x) - m(x)$ with Gaussian kernel and bandwidth $h=0.15$. ANRsimresidual.xpl

Exercises
3.11.1Try the kernel, $k$-$NN$ and spline smoothing on the simulated data set with different smoothing parameters. Describe how you found a ``good" smoothing parameter.

3.11.2Quantify the behavior of the above smoothers at the boundary of the observation interval. Supppose $\vert m'(x) \vert$ is relatively large at the boundary. What do you expect from a local averaging method in this situation?

3.11.1 Complements

In the simulated data set from Table 2 no repeated observations (in the $X$-variable) have been observed. For the case of repeated observations the spline smoothing algorithm of Reinsch (1967) needs some preparatory steps. If one observes multiple responses for a fixed $X=x$ one pools the corresponding $Y$-values into one observation by averaging them. Suppose that there are $N_i \ge 1$ observations at each $X_i$. Then the spline algorithm solves the weighted minimization problem

$$\sum^n_{i=1} (Y_i - g(X_i))^2 / N_i+ \lambda \int [g''(x)]^2 dx.$$