The construction of nearest neighbor estimates differs from that of
kernel estimates.
The kernel estimate ![]() was defined as a weighted average of
the response variables in a fixed neighborhood around
was defined as a weighted average of
the response variables in a fixed neighborhood around ![]() , determined in
shape by the kernel
, determined in
shape by the kernel ![]() and the bandwidth
and the bandwidth ![]() .
The
.
The
![]() -nearest neighbor (
-nearest neighbor (![]() -
-![]() ) estimate is a weighted average in a
varying neighborhood. This neighborhood is defined through those
) estimate is a weighted average in a
varying neighborhood. This neighborhood is defined through those
![]() -variables which are among the
-variables which are among the
![]() -nearest neighbors of
-nearest neighbors of ![]() in Euclidean distance. The
in Euclidean distance. The ![]() -
-![]() weight sequence has been introduced by
Loftsgaarden and Quesenberry (1965) in the related field of density
estimation and has been used by Cover and Hart (1967)
for classification purposes. In the present regression setting the
weight sequence has been introduced by
Loftsgaarden and Quesenberry (1965) in the related field of density
estimation and has been used by Cover and Hart (1967)
for classification purposes. In the present regression setting the
![]() -
-![]() smoother is defined as
smoother is defined as
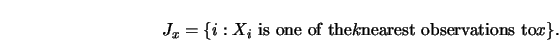
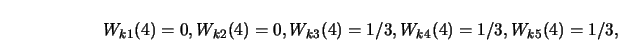
In an experiment in which the ![]() -variable is chosen from an
equidistant grid the
-variable is chosen from an
equidistant grid the ![]() -
-![]() weights are equivalent to kernel weigths.
Let
weights are equivalent to kernel weigths.
Let ![]() and compare
and compare
![]() with
with
![]() for a uniform kernel
for a uniform kernel
![]() for an
for an ![]() not too close to the boundary. Indeed for
not too close to the boundary. Indeed for ![]() :
:
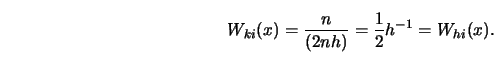
Consider for fixed ![]() the case that
the case that ![]() becomes larger than
becomes larger than ![]() The
The ![]() -
-![]() smoother then is equal to the average of the response variables. The other
limiting case is
smoother then is equal to the average of the response variables. The other
limiting case is ![]() in which the observations are reproduced at
in which the observations are reproduced at ![]() , and
for
an
, and
for
an ![]() between two adjacent predictor variables a step function is obtained
with a jump in the middle between the two observations.
Again a smoothing parameter selection problem is observed:
between two adjacent predictor variables a step function is obtained
with a jump in the middle between the two observations.
Again a smoothing parameter selection problem is observed:
![]() has to be chosen as a function of
has to be chosen as a function of ![]() or even of the data.
As a first goal one might like to reduce the noise by letting
or even of the data.
As a first goal one might like to reduce the noise by letting
![]() tend to infinity as a function of the sample size.
The second goal is
to keep the approximation error (bias) low.
The second goal is achieved if the neighborhood around
tend to infinity as a function of the sample size.
The second goal is
to keep the approximation error (bias) low.
The second goal is achieved if the neighborhood around ![]() shrinks
asymptotically to zero. This can be done by defining
shrinks
asymptotically to zero. This can be done by defining ![]() such that
such that
![]() Unfortunately, this condition conflicts with
the first goal. In order to keep the variance as small as possible one
would like to choose
Unfortunately, this condition conflicts with
the first goal. In order to keep the variance as small as possible one
would like to choose ![]() as large as possible.
as large as possible.
So again we face a trade-off problem between a ``good approximation" to
the regression function and a ``good reduction" of observational noise. This
trade-off problem can be
expressed formally by an expansion of the mean squared error of
the ![]() -
-![]() estimate.
estimate.
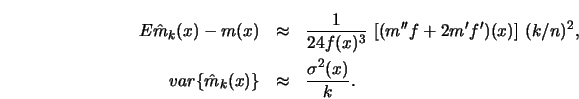
The trade-off between bias![]() and
variance is thus achieved in an asymptotic sense by setting
and
variance is thus achieved in an asymptotic sense by setting
![]() .
A consequence is that the the mean squared error itself
converges to zero at a rate of
.
A consequence is that the the mean squared error itself
converges to zero at a rate of
![]()
Other weight sequences ![]() have been proposed by
Stone (1977).
In addition to the ``uniform" weights (3.4.18) he defined
``triangular and quadratic
have been proposed by
Stone (1977).
In addition to the ``uniform" weights (3.4.18) he defined
``triangular and quadratic ![]() -
-![]() weights."
Generally speaking, the weights can be thought of as being
generated by a kernel function
weights."
Generally speaking, the weights can be thought of as being
generated by a kernel function ![]() ,
,
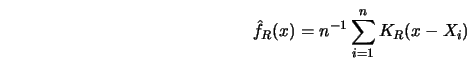

To give insight into this weight sequence consider the potato example
again. In Figure 3.5 the effective ![]() -
-![]() weights
weights ![]() are shown
analogous to the kernel weigths
are shown
analogous to the kernel weigths ![]() in Figure 3.5
in Figure 3.5
![\includegraphics[scale=0.7]{ANRkNNweights.ps}](anrhtmlimg453.gif)
|
One can see quite clearly the difference in the kernel weights.
At the
right end of the data, where the observations get sparser, the ![]() -
-![]() weights
spread out more than the kernel weights, as presented in Figure
3.2
Mack (1981) computes bias and variance for this parameterization of the
weights
weights
spread out more than the kernel weights, as presented in Figure
3.2
Mack (1981) computes bias and variance for this parameterization of the
weights
![]() .
.
A consequence of this proposition is that a balance between the
![]() and the variance contribution to the mean squared error is as for the uniform
and the variance contribution to the mean squared error is as for the uniform
![]() -
-![]() weights (3.4.19) achieved by
letting
weights (3.4.19) achieved by
letting ![]() be proportional to
be proportional to ![]() .
Thinking of the
bandwidth
parameter
.
Thinking of the
bandwidth
parameter ![]() for kernel smoothers as being roughly
equivalent to
for kernel smoothers as being roughly
equivalent to
![]() it is
seen that the bias and variance rates of
it is
seen that the bias and variance rates of ![]() are completely
equivalent to those for kernel smoothers, only the constants differ.
The bias of
are completely
equivalent to those for kernel smoothers, only the constants differ.
The bias of ![]() tends to be large in the tail of the marginal distribution.
The kernel estimators show
a different behavior: There the variance is a multiple of
tends to be large in the tail of the marginal distribution.
The kernel estimators show
a different behavior: There the variance is a multiple of ![]() and the bias turns out not to be a function of
and the bias turns out not to be a function of ![]() .
A comparison of kernel and
.
A comparison of kernel and ![]() -
-![]() smoothers mean squared error properties can
be found in Table 3.1
smoothers mean squared error properties can
be found in Table 3.1
| kernel | ||
| bias |
|
|
| variance |
|
|
The entries of Table 3.1
show the asymptotic dependence of bias and variance on
![]() and
and ![]() .
The essential equivalence of the row entries of Table 3.2.1 can be seen
by using the relation
.
The essential equivalence of the row entries of Table 3.2.1 can be seen
by using the relation
A third kind of ![]() -
-![]() smoothers are symmetrized nearest neighbor
estimators. Let
smoothers are symmetrized nearest neighbor
estimators. Let ![]() denote the empirical distribution of the sample from
denote the empirical distribution of the sample from
![]() Let
Let ![]() be a bandwidth tending to zero. The estimate proposed by
Yang (1981) and studied by Stute (1984) is
be a bandwidth tending to zero. The estimate proposed by
Yang (1981) and studied by Stute (1984) is
The estimate (3.4.23) is
also a nearest neighbor estimate, but now neighbors are defined in terms of
distance based on the empirical distribution function of the
![]() . Thus a weight sequence
(symmetric in
. Thus a weight sequence
(symmetric in ![]() space)
space)
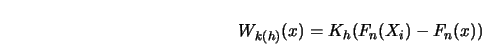
Note that ![]() always averages over a symmetric neighborhood in the
always averages over a symmetric neighborhood in the
![]() -space, but may have an asymmetric neighborhood of
-space, but may have an asymmetric neighborhood of ![]() .
By contrast,
.
By contrast, ![]() always averages over the same amount of points left and right of
always averages over the same amount of points left and right of ![]() ,
but may in effect average over an asymmetric neighborhood in the
,
but may in effect average over an asymmetric neighborhood in the ![]() -space.
The estimate
-space.
The estimate ![]() has an intriguing relationship with the
has an intriguing relationship with the ![]() -
-![]() estimator used by Friedman (1984).
The variable span smoother (supersmoother)
proposed by Friedman uses the same type of
neighborhood as does
estimator used by Friedman (1984).
The variable span smoother (supersmoother)
proposed by Friedman uses the same type of
neighborhood as does ![]() ; see Section 5.3.
The estimate (3.4.23)
also looks appealingly like a kernel regression estimate of
; see Section 5.3.
The estimate (3.4.23)
also looks appealingly like a kernel regression estimate of ![]() against not
against not ![]() but rather
but rather ![]() .
Define the expected value
.
Define the expected value
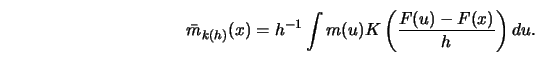
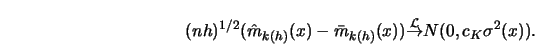
With this choice of
![]() has the same limit properties as a kernel or ordinary
nearest neighbor estimate as long as its bias term is of order
has the same limit properties as a kernel or ordinary
nearest neighbor estimate as long as its bias term is of order ![]() .
It is in fact not hard to show that the bias satisfies to order
.
It is in fact not hard to show that the bias satisfies to order ![]() :
:

Otherwise, the smoothing parameter balancing variance versus bias![]() for the kernel and ordinary
nearest neighbor estimates will lead to a different mean squared error than
what one obtains for the symmetrized nearest neighbor estimate.
An example is given in Figure 3.6
for the kernel and ordinary
nearest neighbor estimates will lead to a different mean squared error than
what one obtains for the symmetrized nearest neighbor estimate.
An example is given in Figure 3.6
![\includegraphics[scale=0.7]{ANRsimnn.ps}](anrhtmlimg486.gif)
|
For these data, we used the quartic kernel
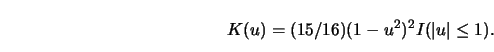
A great advantage of the ![]() -
-![]() estimate (3.4.18) is that its
computation can be updated quite easily when
estimate (3.4.18) is that its
computation can be updated quite easily when ![]() runs along the sorted
array of
runs along the sorted
array of ![]() -variables. The algorithm requires essentially
-variables. The algorithm requires essentially ![]() operations to compute the smooth at all
operations to compute the smooth at all ![]() , as compared to
, as compared to ![]() operations for direct computation of the kernel estimate.
operations for direct computation of the kernel estimate.
Let us construct ![]() -
-![]() smoothers as weighted averages over a fixed
number of observations with uniform weights as
used as in (3.4.19). Suppose that the data have been
pre-sorted, so that
smoothers as weighted averages over a fixed
number of observations with uniform weights as
used as in (3.4.19). Suppose that the data have been
pre-sorted, so that
![]() .
Then if the
estimate has already been computed at some point
.
Then if the
estimate has already been computed at some point ![]() the
the ![]() -
-![]() smoother at
smoother at ![]() can be recursively determined as
can be recursively determined as
![\begin{displaymath}\hat m_k(X_{i+1})= \hat m_k(X_i)+ k^{-1}(Y_{i+[k/2] +1} - Y_{i- [k/2]}),\end{displaymath}](anrhtmlimg496.gif)
This updating formula is also
applicable for local polynomial fits. For simplicity only the local
linear fit is described . The slope ![]() and intercept
and intercept ![]() of
the least squares line through the neighborhood determined by uniform
weights (3.4.19) are given by
of
the least squares line through the neighborhood determined by uniform
weights (3.4.19) are given by
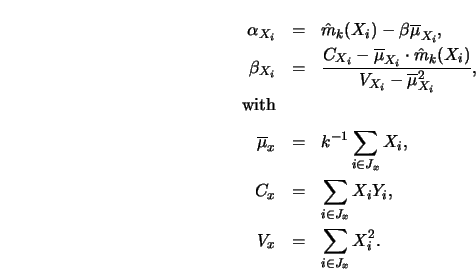
![\begin{eqnarray*}
\overline \mu_{X_{i+1}}
&=&\overline \mu_{X_i} + k^{-1} (X_{i...
...
V_{X_{i+1}}
&=& V_{X_i} + X^2_{i+ [k/2] +1} -X^2_{i- [k/2]}.
\end{eqnarray*}](anrhtmlimg503.gif)
This recursive algorithm is a component of the supersmoother to be described in Section 5.3.
The principal idea of updating also applies to the ![]() -
-![]() estimate
estimate ![]() if a discrete approximation to the kernel
if a discrete approximation to the kernel ![]() is
used. Suppose that for fixed
is
used. Suppose that for fixed ![]() the effective kernel weight is
sufficiently well approximated by a sum of indicator functions
the effective kernel weight is
sufficiently well approximated by a sum of indicator functions
![\begin{displaymath}(2 [k/2])^{-1} \sum^{[k/2]}_{j=0} I (\left\vert x-X_i
\right\vert \le
R_n(k-2j)),\end{displaymath}](anrhtmlimg505.gif)
![\begin{displaymath}\hat m_R(x) \approx (2 [k/2])^{-1} \sum^{[k/2]}_{j=0} \hat
m_{k-2j}(x).\end{displaymath}](anrhtmlimg507.gif)
Exercises
3.4.1Show that the bias and variance of ![]() are identical to the bias and variance of
are identical to the bias and variance of ![]() if a uniform kernel is used.
if a uniform kernel is used.
3.4.2Define ![]() variance
variance![]() bias
bias![]() .
Compute
.
Compute

3.4.3Implement the ![]() -
-![]() algorithm on a computer and compare with a brute force programming of the kernel
smoother. Where do you see numerical advantages or disadvantages of the
recursive updating algorithm?
algorithm on a computer and compare with a brute force programming of the kernel
smoother. Where do you see numerical advantages or disadvantages of the
recursive updating algorithm?
3.4.4Compare kernel and ![]() -
-![]() smoothes subjectively.
At what regions of the data would you prefer the one before the other?
smoothes subjectively.
At what regions of the data would you prefer the one before the other?
3.4.5Verify the bias formula (3.4.24) for the symmetrized nearest neighbor
estimator. Compare with the bias for the ordinary ![]() -
-![]() smoother and the
kernel smoother.
smoother and the
kernel smoother.