4. How close is the smooth to the true curve?

                It was, of course, fully recognized that the estimate might differ from the parameter in any particular case, and hence that there was a margin of uncertainty. The extent of this uncertainty was expressed in terms of the sampling variance of the estimator.

Sir M. Kendall and A. Stuart (1979, p. 109)

If the smoothing parameter is chosen as a suitable function of the sample size $n$, all of the above smoothers converge to the true curve if the number of observations increases. Of course, the convergence of an estimator is not enough, as Kendall and Stuart in the above citation say. One is always interested in the extent of the uncertainty or at what speed the convergence actually happens. Kendall and Stuart (1979) aptly describe the procedure of assessing measures of accuracy for classical parametric statistics: The extent of the uncertainty is expressed in terms of the sampling variance of the estimator which usually tends to zero at the speed of the square root of the sample size $n$.

In contrast to this is the nonparametric smoothing situation: The variance alone does not fully quantify the convergence of curve estimators. There is also a bias present which is a typical situation in the context of smoothing techniques. This is the deeper reason why up to this Section the precision has been measured in terms of pointwise mean squared error (MSE), the sum of variance and squared bias. The variance alone doesn't tell us the whole story if the estimator is biased.

We have seen, for instance, in Section 3.4 , that the pointwise MSE

$$E [{\hat{m}}(x)-m(x) ]^2,$$

tends to zero for the $k$-$NN$ smoother ${\hat{m}}_k$, if $k \to \infty$ and $k/n \to 0$. There are some natural questions concerning this convergence. How fast does the MSE tend to zero? Why should the measure of accuracy only be computed at one single point? Why not investigate a more ``global'' measure like the mean integrated squared error (MISE)? It is the purpose of this chapter to present several of such distance measures for functions and to investigate the accuracy of ${\hat{m}}(\cdot)$ as an estimate of $m(\cdot)$ in a uniform and pointwise sense. In this chapter the response variable can also be a multidimensional variable in $\mathbb{R}^d$.

A variety of ``global'' distance measures can be defined. For instance, the integrated absolute deviation (weighted by the marginal density $f$)

$$d_{L_1} ({\hat{m}}, m)=\int \left\vert {\hat{m}}(x)-m(x) \right\vert f(x) d x$$

has been shown Devroye and Wagner (1980a, 1980b) to converge almost surely to zero for kernel estimators ${\hat{m}}(x)$. Devroye and Györfi (1985) demonstrate an analogous result for the regressogram.

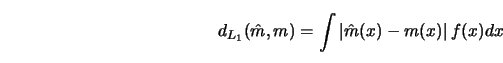
Another distance is defined through the maximal absolute deviation,

$$d_{L_\infty} ({\hat{m}}, m)=\sup_{x \in {\cal X}} \left\vert {\hat{m}}(x)-m(x) \right\vert ,$$

where the $\sup_x$ ranges over a set ${\cal X}\in \mathbb{R}^d$ of interest. Devroye (1978), Mack and Silverman (1982) and Härdle and Luckhaus (1984) investigated the speed at which this distance tends to zero for kernel estimators.

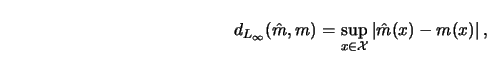
Quadratic measures of accuracy have received the most attention. A typical representative is the Integrated Squared Error (ISE)

$$d_I ({\hat{m}}, m)=\int ({\hat{m}}(x)-m(x))^2 f(x) w(x) d x,$$

where $w$ denotes a weight function. A discrete approximation to $d_I$ is the Averaged Squared Error (ASE)

$$d_A ({\hat{m}}, m)=n^{-1} \sum^n_{i=1} ({\hat{m}}(X_i)-m(X_i))^2 w(X_i).$$

In practice this distance is somewhat easier to compute than the distance measure $d_I$ since it avoids numerical integration. A conditional version of $d_A$

$$d_C ({\hat{m}}, m)=E \{d_A ({\hat{m}}, m) \vert X_1,\ldots, X_n \}$$

has also been studied. The distance $d_C$ is a random distance through the distribution of the $X$s. Taking the expectation of $d_I$ with respect to $X$ yields the MISE

$$d_M ({\hat{m}}, m)=E \{d_I ({\hat{m}}, m)\}.$$

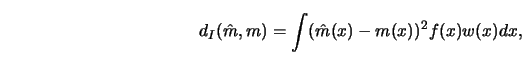
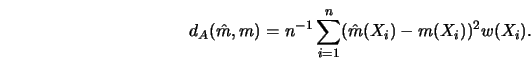
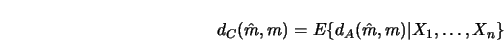
In order to simplify the presentation I will henceforth consider only kernel estimators. Most of the error calculations done for kernel smoothers in Section 3.1 can be extended in a straightforward way to show that kernel smoothers converge in the above global measure of accuracy to the true curve. But apart from such desirable convergence properties, it is important both from a practical and a theoretical point of view to exactly quantify the speed of convergence over a class of functions. This is the subject of the next section. In Section 4.2 pointwise confidence intervals are constructed. Global variability bands and error bars are presented in Section 4.3. The boundary problem, for example, the fact that the smoother behaves qualitatively different at the boundary is discussed in Section 4.4. The selection of kernel functions is presented in Section 4.5. Bias reduction techniques by the jackknife method are investigated in Section 4.6.