4.6 Bias reduction techniques

In this section we will see that the use of ``higher order kernels'' has the nice effect of reducing the bias. The kernels of Figure 1.3 are of higher order. The spline smoothing kernel (Figures 3.10,3.11), for instance, is of order $(0,4)$. (The order of a kernel was defined in the previous section.) Another technique for bias reduction is jackknifing. I shall explain subsequently how jackknifing is related to higher order kernels and investigate the variance of higher order kernel smoothers.

Consider the fixed design model of equispaced and fixed $\{X_i=i/n \}$ on the unit interval. Suppose that it is desired to estimate the $k$th derivative $m^{(k)}$ of $m$. The kernel smoother for this problem is

$${\hat{m}}_h^{(k)}(x)=n^{-1}h^{-(k+1)}\ \sum_{i=1}^n K^{(k)} \left({x-X_i \over h}\right) Y_i \, \quad 0<x<1,$$

where $K^{(k)}$ is the $k$th derivative of a $k$-times differentiable kernel $K$ for which it is required that

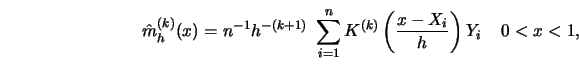
$$\begin{eqnarray*} \hbox{support}(K)&=&[-1,1];\cr K^{(j)}(1)=K^{(j)}(-1)&=&0 \, \quad j=0,\ldots,(k-1). \end{eqnarray*}$$

Let $m$ be $p$-times $(p \ge k+2)$ differentiable and suppose that the kernel $K$ is such that for some constant $C_K$

$$\int_{-1}^1 K(u)u^j \ du = 0, \quad j=1,\ldots,p-k-1;\cr$$ (4.6.30)

Then $K^{(k)}$ satisfies

$$\begin{array}{rll} \int_{-1}^1 K^{(k)}(u)u^j\ d u&=0,&j=0,\l... ...,\ldots,p-1;\cr &=(-1)^k k!,&j=k;\cr &=C_K,&j=p. \end{array}$$ (4.6.31)

The expectation of ${\hat{m}}_h^{(k)}(x)$ can be approximated as in 3.3.17 or 4.1.1 by

$$\int_{-1}^1 K(u)m^{(k)}(x-u h)d u \, \quad 0<x<1$$ (4.6.32)

Expanding $m^{(k)}(x-u h)$ in a Taylor series around $x$ one sees from 4.6.32 and 4.6.31 that with a kernel function satisfying 4.6.30 the bias of ${\hat{m}}_h^{(k)}(x)$ is, to first order, equal to

$${h^{(p-k)}\over p!}\ \left[ \int_{-1}^1 K^{(k)} (u)u^p\ d u \right] m^{(p)}(x).$$ (4.6.33)

By increasing $p$, the degree of differentiability and the order of the kernel, one can make this quantity arbitrarily small. This technique is commonly called bias reduction through ``higher order kernels''.

Higher order kernel functions $K^{(k)}$ satisfy 4.6.32 with a large value of $p$ (Müller 1984a; Sacks and Ylvisaker 1981). This means that $K^{(k)}$ has the first $(k-1)$ moments and then the $(k+1)$th up to the $(p-1)$th moment vanishing.

Since higher order kernels take on negative values the resulting estimates inherit this property. For instance, in the related field of density estimation, kernel smoothing with higher order kernels can result in negative density estimates. Also, in the setting of regression smoothing one should proceed cautiously when using higher order kernels. For example, in the expenditure data situation of Figure 2.3 the estimated expenditure Engel curve could take on negative values for a higher order kernel. For this reason, it is highly recommended to use a positive kernel though one has to pay a price in bias increase.

It seems appropriate to remind the reader that ``higher order'' kernels reduce the bias in an asymptotic sense. Recall that when estimating $m$, the optimal rate of convergence (Section 4.1) for kernels with $p=2$ is $n^{-2/5}$. If a kernel with $p=4$ is used, then the optimal rate is $n^{-4/9}$. So using a ``higher order'' kernel results in a relatively small improvement $(2/45)$ in the order of magnitude of the best achievable squared error distance. For all except astronomical sample sizes this difference will become visible. Higher order kernels have other undesirable side effects as can be seen from the following discussion of the jackknifing approach.

Schucany and Sommers (1977) construct a jackknife kernel density estimator that yields a bias reducing kernel of higher order. The jackknife technique is also applicable for bias reduction in regression smoothing. Consider the jackknife estimate (Härdle 1986a)

$$G({\hat{m}}_{h_1}, {\hat{m}}_{h_2}) (x)=(1-R)^{-1} [ {\hat{m}}_{h_1} (x)-R {\hat{m}}_{h_2} (x) ],$$

where $R \not=1$ is a constant. Here ${\hat{m}}_{h_l} (x)$ is a kernel smoother with bandwidth $h_l, l=1,2$. Suppose that the kernel $K$ is of order 2, that is, satisfies 4.6.31 with $p=2$ and the regression function is four-times differentiable. Then the bias term of the jackknife estimate $G({\hat{m}}_{h_1}, {\hat{m}}_{h_2})$ can be expressed as:

$$(1-R)^{-1} \sum^2_{j=1} [ h_1^{2 j}-R h_2^{2 j} ] C_j(K) m^{(2 j)} (x).$$ (4.6.34)

A good choice of $R$ reduces this bias an order of magnitude. Define

$$R=h^2_1/h^2_2,$$

making the coefficient of $m^{(2)} (x)$ in 4.6.34 zero. Indeed, the bias of $G({\hat{m}}_{h_1}, {\hat{m}}_{h_2})$ has been reduced compared with the bias of each single kernel smoother. Moreover, the jackknife estimator with this $R$, being a linear combination of kernel smoothers, can itself be defined by a kernel

$$K_{(c)}(u)={K(u)-c^3 K(c u) \over (1-c^2)}$$

with

$$c=h_1/h_2=\sqrt R.$$

Note that $K_{(c)}$ depends on $n$ through $c$. The bias reduction by $K_{(c)}$ can also be seen by calculations as in Section 4.6. $K_{(c)}$ is indeed a ``higher order'' kernel satisfying 4.6.31 with $p=4$ but is not optimal in the sense of minimizing $V(K)B(K)$. By l'Hospital's rule the limit of $K_{(c)}$ as $c \to 1$ is

$$K_{(1)}(u)={3 \over 2} K(u)+{1 \over 2} u K'(u)$$

at points where $K$ is differentiable.

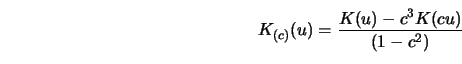
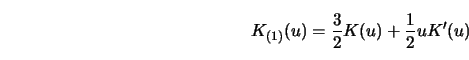
At first sight the use of the jackknife technique seems to be a good strategy. If at the first step only a small amount of smoothness is ascribed to $m$ then in a further step the jackknife estimate will indeed reduce the bias, provided that $m$ is four-times differentiable. However, a sharper analysis of this strategy reveals that the variance (for fixed $n$) may be inflated.

Consider the Epanechnikov kernel

$$K(u)=(3/4)(1-u^2) I (\left \vert u \right \vert \le 1).$$

Straightforward computations show that

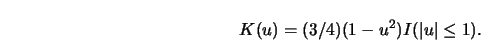
$$\begin{eqnarray*} c_K&=&\int K^2 (u)d u=3/5,\cr \int K^2_{(c)} (u)d u&=&{{9 \over 10} [ c^3+2 c^2+4/3 c+2/3 ] \over [ c+1 ]^2} \end{eqnarray*}$$

Table 4.4 shows the dependence of this number on $c$ together with the increase in variance compared to $K$.

Table: The variance component $\int K^2_{(c)}(u)d u$ of the effective kernel as a function of $c$, and the relative deficiency $\int K^2_{(c)}(u)d u/\int K^2(u)d u$ with respect to the Epanechnikov kernel.

$c$	$\int K^2_{(c)}(u)d u$	${\int K^2_{(c)}(u)d u \over \int K^2(u)d u}$
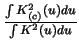0.10	0.610	1.017
0.20	0.638	1.063
0.30	0.678	1.130
0.40	0.727	1.212
0.50	0.783	1.305
0.60	0.844	1.407
0.70	0.900	1.517
0.80	0.979	1.632
0.90	1.050	1.751
0.91	1.058	1.764
0.92	1.065	1.776
0.93	1.073	1.788
0.94	1.080	1.800
0.95	1.087	1.812
0.96	1.095	1.825
0.97	1.102	1.837
0.98	1.110	1.850
0.99	1.117	1.862

It is apparent from these figures that some caution must be exercised in selecting $c$ (and $R$), since the variance increases rapidly as $c$ tends to one. In order to compare the mean squared error of ${\hat{m}}_h$ with that of $G({\hat{m}}_{h_1}, {\hat{m}}_{h_2})$ one could equalize the variances by setting

$$h_1=\left[ \int K^2_{(c)} (u)d u/\int K^2(u)d u \right] h.$$

Without loss of generality one can assume that $m^{(2)} (x)/10=m^{(4)} (x)/280=1$. The leading bias term of ${\hat{m}}_h$ is then $h^2+h^4$, whereas that of $G({\hat{m}}_{h_1}, {\hat{m}}_{h_2})$ for $c=0.99$ is equal to $\sqrt{152.76} h^4$. So, if $h^2>1/(\sqrt{152.76}-1)$ the jackknifed estimator is less accurate than the ordinary kernel smoother.

Since the choice of $R$ (and $c$) seems to be delicate in a practical example, it is interesting to evaluate the jackknifed estimator in a simulated example. Suppose that $m(x)=\sin(x), n=100, \sigma^2=1$ and it is desired to evaluate the mean squared error at $x=\pi/4$. A bandwidth $h$, being roughly equal to 0.3, would minimize the mean squared error of ${\hat{m}}_h(x)$ (with the Epanechnikov kernel). Table 4.5 shows the ratio of the mean squared error of $G({\hat{m}}_{h_1}, {\hat{m}}_{h_2})$ to that of ${\hat{m}}_h$ as $c$ and $h$ are varied.

The efficiency of the jackknifed kernel smoother $G[\hat{m}_{h_1},\hat{m}_{h_2}]$ with respect to the ordinary kernel estimator

Table 4.5:

	$c=0.1$			$c=0.2$			$c=0.3$
$h\backslash h_1$	0.2	0.3	0.4	0.2	0.3	0.4	0.2	0.3	0.4
0.2	1.017	0.67	0.51	1.063	0.709	0.532	1.13	0.753	0.565
0.3	1.52	1.017	0.765	1.59	1.063	0.798	1.695	1.13	0.847
0.4	2.035	1.357	1.020	2.127	1.418	1.064	2.26	1.507	1.13
	$c=0.4$			$c=0.5$			$c=0.6$
$h\backslash h_1$	0.2	0.3	0.4	0.2	0.3	0.4	0.2	0.3	0.4
0.2	1.212	0.808	0.606	1.305	0.87	0.652	1.407	0.938	0.703
0.3	1.818	1.212	0.909	1.958	1.305	0.979	2.111	1.407	1.055
0.4	2.424	1.616	1.212	2.611	1.74	1.305	2.815	1.877	1.407
	$c=0.7$			$c=0.8$			$c=0.9$
$h\backslash h_1$	0.2	0.3	0.4	0.2	0.3	0.4	0.2	0.3	0.4
0.2	1.517	1.011	0.758	1.632	1.088	0.816	1.751	1.167	0.875
0.3	2.275	1.517	1.137	2.448	1.632	1.224	2.627	1.751	1.313
0.4	3.034	2.022	1.517	3.264	2.176	1.632	3.503	2.335	1.751

Note: Shown is the ratio: mean squared error $\{G[\hat{m}_{h_1},\hat{m}_{h_2}]\}/$ mean squared error $\{\hat{m}_h\}$ (for $n=100, m(x)=\sin(x),\sigma^2=1,$ and $x=\pi/4$) as a function of $c$, $h$ and $h_1$.
Source: Härdle (1986a), © 1986 IEEE.

The use of the higher order kernel technique, as is done by the jackknife technique, may thus result in a mean squared error nearly twice as large as the corresponding error of the ordinary Epanechnikov kernel smoother, as can be seen from the entry $(h, h_1,c)=(0.3,0.3,0.9)$ in Table 4.5.

Exercises
4.6.1 Why is it impossible to find a positive symmetric kernel of order $(0,4)$?

4.6.2 Compute the $c_K$ for higher order kernels of order $(0,p)$ as a function of $p$. Do you observe an increasing value of $c_K$ as $p$ increases?