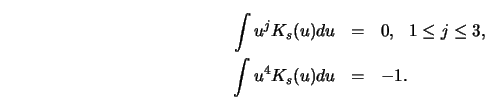There are several ways to quantify local variation.
One could define measures of
roughness based, for instance, on the
first, second, and so forth derivative. In order to explicate the main ideas
the integrated squared second derivative is most convenient, that is, the
roughness penalty

![]() is a cubic polynomial
between two successive
is a cubic polynomial
between two successive ![]() -values;
at the observation points
-values;
at the observation points ![]() the curve
the curve
![]() and its first two derivatives are continuous
but there may be a discontinuity in the third derivative;
and its first two derivatives are continuous
but there may be a discontinuity in the third derivative;
at the boundary points ![]() and
and ![]() the second derivative of
the second derivative of
![]() is zero.
is zero.
pt It should be noted that these properties follow from the particular choice of the roughness penalty. It is possible to define, say, quintic splines by considering a roughness penalty that involves higher-order derivatives.
An example of a spline smooth is given in Figure 3.9, a spline smooth of the so-called motorcycle data set, see Table 1 in the Appendix 2 for a complete listing of this data set.
![\includegraphics[scale=0.7]{ANRmotspline.ps}](anrhtmlimg588.gif)
|
Recall that the spline is a cubic polynomial between the knot points.
The ``local cubic polynomial"
property is illustrated in Figure 3.10 where at three
significant points the (local) cubic polynomial fit is superimposed
on the spline smooth, computed from the motorcycle data set.
The curve shown is computed at the points
![]() itself
using the IMSL routine ICSSCU. The motorcycle data set is listed in Table 1
in the Appendix 2.
itself
using the IMSL routine ICSSCU. The motorcycle data set is listed in Table 1
in the Appendix 2.
![\includegraphics[scale=0.7]{ANRmotcubic.ps}](anrhtmlimg595.gif)
|
A conceptual difficulty in spline smoothing is the fact that
![]() is defined implicitly as the solution to a functional
minimization problem.
This makes it hard to judge the behavior of the estimate and to see
what
is defined implicitly as the solution to a functional
minimization problem.
This makes it hard to judge the behavior of the estimate and to see
what
![]() is actually doing to the data values.
The following argument shows that
is actually doing to the data values.
The following argument shows that
![]() is, in fact, a
weighted average of the
is, in fact, a
weighted average of the ![]() -observations.
-observations.
The minimum of
![]() is unique, so we must have
is unique, so we must have
![]() for
any
for
any ![]() and
and ![]() .
This means that the real function
.
This means that the real function
![]() has a local minimum
at
has a local minimum
at ![]() . In particular, the Euler-Lagrange condition (Hadley and
Kemp 1971, p. 30-31),
. In particular, the Euler-Lagrange condition (Hadley and
Kemp 1971, p. 30-31),
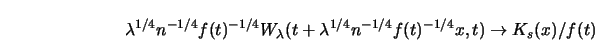
pt
The approximation of
![]() in the above
Theorem says that for large
in the above
Theorem says that for large ![]() and small
and small ![]() and
and ![]() not too
close to the boundary,
not too
close to the boundary,
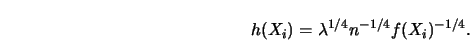
![\includegraphics[scale=0.7]{ANRsplinekernel.ps}](anrhtmlimg634.gif)
|
One sees that ![]() is a symmetric kernel
function with negative side lobes and that
is a symmetric kernel
function with negative side lobes and that ![]() has vanishing
second moment, that is,
has vanishing
second moment, that is,
![]() .
A graphical comparison of the exact weight function
.
A graphical comparison of the exact weight function
![]() and its asymptotic form
and its asymptotic form ![]() is given
in Silverman (1984, figure 2, p. 902).
is given
in Silverman (1984, figure 2, p. 902).
The kernel form of this weight function changes as ![]() approaches the
boundary of the observation interval. Engle et al. (1986) computed the
effective spline weight function for the temperature response example (see
Figure 1.6). Figure 3.12 is a reproduction from their article where they
show the equivalent kernel function for an
approaches the
boundary of the observation interval. Engle et al. (1986) computed the
effective spline weight function for the temperature response example (see
Figure 1.6). Figure 3.12 is a reproduction from their article where they
show the equivalent kernel function for an ![]() roughly in the middle of the
observation interval.
roughly in the middle of the
observation interval.
![\includegraphics[scale=0.2]{ANR3,12.ps}](anrhtmlimg639.gif)
|
As the observation point moves to the right the weight function becomes more asymmetric as Figure 3.13 indicates.
![\includegraphics[scale=0.6]{ANR3,13.ps}](anrhtmlimg642.gif)
|
The question of how much to smooth is of course also to be posed for spline
smoothing. A survey of the literature on the mean squared error properties of
spline smoothing can be found in Eubank (1988). The smoothing parameter
selection problem for this class of estimators has been mainly investigated
by Grace Wahba. From her rich collection of results I would like to mention
those which are directly connected with the optimization of ![]() In
Wahba (1975), Wahba (1979) convergence rates of splines are considered. The
pioneering article on cross-validation in this context is Wahba (1975), which was extended later to the smoothing of the log periodogram;
(see Wahba; 1980). The term generalized cross-validation (GCV) was coined by
Wahba (1977). A minimax type approach to the question of rates of convergence was
done by Nussbaum (1985) who obtained exact bounds for the integrated squared
error under a normality assumption on the error variables.
In
Wahba (1975), Wahba (1979) convergence rates of splines are considered. The
pioneering article on cross-validation in this context is Wahba (1975), which was extended later to the smoothing of the log periodogram;
(see Wahba; 1980). The term generalized cross-validation (GCV) was coined by
Wahba (1977). A minimax type approach to the question of rates of convergence was
done by Nussbaum (1985) who obtained exact bounds for the integrated squared
error under a normality assumption on the error variables.
Some statistical software packages that
compute the spline coefficients of the local
cubic polynomials require a bound ![]() on the residual sum of
squares
on the residual sum of
squares
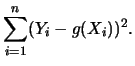 These programs
solve the equivalent problem
These programs
solve the equivalent problem

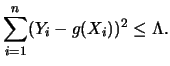 The parameters
The parameters

This correspondence is derived explicitly for the example given in
Section 3.11.
The same methods can be used to derive an equivalent ![]() for a
given smoothing parameter
for a
given smoothing parameter ![]()
The effective weights of spline smoothing can be more easily computed for
equispaced uniform ![]() .
In this situation the
.
In this situation the ![]() -
-![]() estimator
estimator ![]() and the kernel
estimator
and the kernel
estimator ![]() coincide for
coincide for ![]() roughly equal to
roughly equal to ![]() .
Huber (1979) showed under a periodicity assumption on
.
Huber (1979) showed under a periodicity assumption on ![]() that the spline smoother is exactly
equivalent to a weighted kernel-type average of the
that the spline smoother is exactly
equivalent to a weighted kernel-type average of the ![]() -observations.
He considers
the following function of
-observations.
He considers
the following function of
![]()
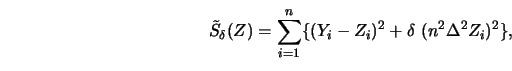
![\includegraphics[scale=0.14]{ANR3,14.ps}](anrhtmlimg667.gif)
|
The curves in Figure 3.14 look indeed very similar to the one in Figure 3.10
Exercises
3.6.1 Use the spline smoothing algorithm to plot the exact weight function
![]() Compare with the approximate function given by
Compare with the approximate function given by
![]() . How does the approximation change when
. How does the approximation change when ![]() moves to the boundary?
moves to the boundary?
3.6.2Show that the kernel ![]() is a kernel in the sense of Section
3.1 and
prove that
is a kernel in the sense of Section
3.1 and
prove that