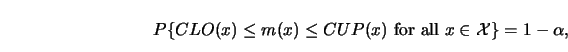 |
(4.3.13) |
There are several approaches to computing upper and lower bands, ![]() and
and ![]() . One approach is to use pointwise confidence intervals on a
very fine grid of the observation interval. The level of these confidence
intervals can be adjusted by the Bonferroni method in order to obtain uniform
confidence bands. The gaps between the grid points can be bridged via
smoothness conditions on the regression curve.
. One approach is to use pointwise confidence intervals on a
very fine grid of the observation interval. The level of these confidence
intervals can be adjusted by the Bonferroni method in order to obtain uniform
confidence bands. The gaps between the grid points can be bridged via
smoothness conditions on the regression curve.
Another approach is to consider
![]() as a stochastic process (in
as a stochastic process (in
![]() ) and then to derive asymptotic Gaussian approximations to that process.
The extreme value theory of Gaussian processes yields the level of these
confidence bands.
) and then to derive asymptotic Gaussian approximations to that process.
The extreme value theory of Gaussian processes yields the level of these
confidence bands.
A third approach is based on the bootstrap. By resampling one attempts to
approximate the distribution of
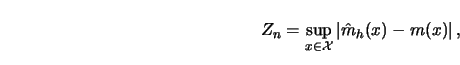
The approach by Hall and Titterington (1986b) is based on the discretization
method, that is, constructing simultaneous error bars at different locations.
They considered a fixed design regression model on the unit interval, that is,


Divide the region of interest into ![]() cells, the
cells, the ![]() th cell containing those
observations
th cell containing those
observations ![]() such that
such that
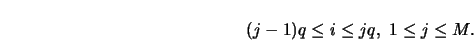
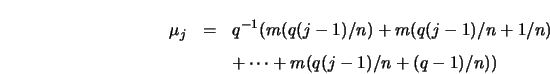
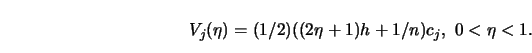
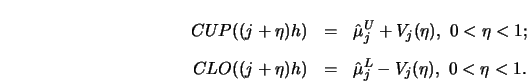
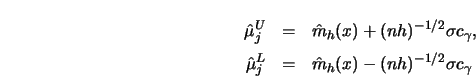
If the error variance is not known, Hall and Titterington (1986b) recommend
constructing an estimate of ![]() using differences of observations, that
is
using differences of observations, that
is
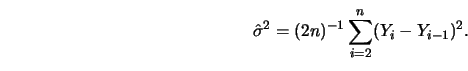
Algorithm 4.3.1
Define the ![]() cells and compute the kernel estimator as in
4.3.15.
cells and compute the kernel estimator as in
4.3.15.
STEP 1.
Define
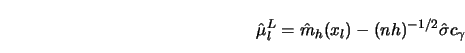
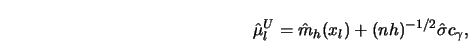
STEP 2.
Let the bound of variation be
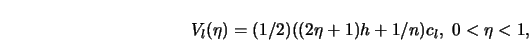
STEP 3.
Define as in 4.3.18
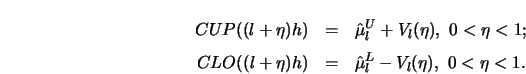
STEP 4.
Draw ![]() and
and ![]() around
around
![]() .
.
The band
![]() is a level
is a level ![]() uniform confidence
band for
uniform confidence
band for ![]() as was shown by Hall and Titterington (1986b). The discretization
method was also employed by Knafl, Sacks and Ylvisaker (1985) and Knafl et al.
(1984).
as was shown by Hall and Titterington (1986b). The discretization
method was also employed by Knafl, Sacks and Ylvisaker (1985) and Knafl et al.
(1984).
Figure 4.5 gives an example of a uniform confidence band for the radiocarbon
data set (Suess 1980). The variables are those of radiocarbon age and tree-ring
age, both measured in years before 1950 A.D. and thinned and rounded so as to
achieve equal spacing of the tree-ring ages.
For more background on this
calibration problem see Scott, Baxter and Aitchison (1984). Altogether, 180
points were included. Hall and Titterington have chosen ![]() so that
so that ![]() .
The bands are constructed with
.
The bands are constructed with ![]() and under the assumption of a
single derivative with uniform bound
and under the assumption of a
single derivative with uniform bound ![]() on
on ![]() .
.
![\includegraphics[scale=0.2]{ANR4,5.ps}](anrhtmlimg1157.gif)
|
A different approach to handling the fluctuation of ![]() in between the
grid points could be based on the arc length of
in between the
grid points could be based on the arc length of ![]() between two successive
knot points. Adrian Bowman suggested that instead of bounding derivatives of
between two successive
knot points. Adrian Bowman suggested that instead of bounding derivatives of
![]() , one could assume an upper bound on the arc length,
, one could assume an upper bound on the arc length,

It was shown in Theorem 4.2.1 that the suitably scaled kernel smoother
![]() has an asymptotic normal distribution,
has an asymptotic normal distribution,
In the setting of nonparametric regression use of this approach was made by
Johnston (1982) for the kernel weights (with known marginal density ![]() )
)
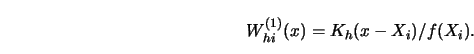
The basic idea of the approach taken by these authors is to standardize the
process
![]() and to approximate it by a suitable
Gaussian process. More precisely, Johnston (1982) has shown that a suitably
rescaled version of
and to approximate it by a suitable
Gaussian process. More precisely, Johnston (1982) has shown that a suitably
rescaled version of
![\begin{displaymath}\sqrt{n h} [{\hat{m}}_h(x)-m(x)]\end{displaymath}](anrhtmlimg1167.gif)
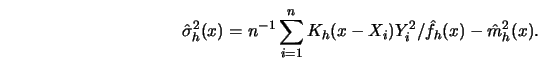
30pt
to 30pt(A1) ![]() and
and ![]() are twice differentiable;
are twice differentiable;
30pt
to 30pt(A2) ![]() is a differentiable kernel with bounded support
is a differentiable kernel with bounded support ![]() ;
;
30pt
to 30pt(A3)
![]() ;
;
30pt
to 30pt(A4) ![]() is strictly positive on
is strictly positive on ![]()
30pt
to 30pt(A5)
![]() .
.
Then the maximal deviation between
![]() and
and ![]() over
over ![]() has
the limiting distribution
has
the limiting distribution
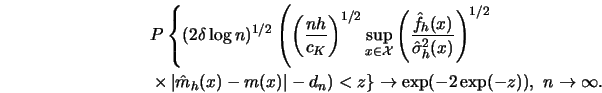
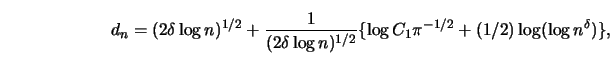

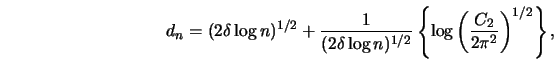

From this theorem one can obtain approximate confidence bands for ![]() . Take
the quartic kernel
. Take
the quartic kernel
![]() , for
instance. For this kernel
, for
instance. For this kernel ![]() and it vanishes at the boundary of its
support
and it vanishes at the boundary of its
support ![]() , so
, so ![]() in the Theorem 4.3.. The following algorithm
is designed for the quartic kernel.
in the Theorem 4.3.. The following algorithm
is designed for the quartic kernel.
Define from ![]() and
and
![]()
![\begin{eqnarray*}
d_n&=&(2 \log 1/h)^{1/2}+(2 \log 1/h)^{-1/2} \log\left({C_2 \o...
...
&&\times[{\hat{\sigma}}^2_h(x)/({\hat{f}}_h(x) n h)]^{1/2}/c_K
\end{eqnarray*}](anrhtmlimg1189.gif)

STEP 2.
Plot the asymptotic confidence bands ![]() and
and ![]() around
around
![]() .
.
pt
Note that this theorem does not involve a bias correction as in Algorithm
4.3.1. The bias term is suppressed by assuming that the bandwidth ![]() tends to
zero slightly faster than the optimal rate
tends to
zero slightly faster than the optimal rate ![]() . A bias term could be
included, but it has the rather complicated form 4.2.8; see Theorem
4.2.1. A
means of automatically correcting for the bias is presented subsequently in the
wild bootstrapping algorithm.
. A bias term could be
included, but it has the rather complicated form 4.2.8; see Theorem
4.2.1. A
means of automatically correcting for the bias is presented subsequently in the
wild bootstrapping algorithm.
Figure 4.6 shows an application of Algorithm 4.3.2, a uniform confidence
band for the expenditure Engel curve for food with ![]() .
.
![\includegraphics[scale=0.14]{ANR4,6.ps}](anrhtmlimg1196.gif)
|
The idea of bootstrap bands is to approximate the distribution of

REPEAT
b=b+1
STEP 1.
Sample
![]() from the data
from the data
![]() .
.
STEP 2.
Construct a kernel smooth
![]() from the bootstrap sample
from the bootstrap sample
![]() and define
and define
![]() .
.
UNTIL b=B (=number of bootstrap samples).
STEP 3.
Define ![]() as the
as the ![]() quantile of the B bootstrap deviations
quantile of the B bootstrap deviations
![]() . By analogy, define
. By analogy, define ![]() as the
as the ![]() quantile.
quantile.
STEP 4.
Draw the interval
![]() around every point
around every point ![]() of the
observation interval.
of the
observation interval.
pt
The above algorithm is extremely computer intensive since on a fine grid of
points the statistic ![]() has to be computed
has to be computed ![]() times. A computationally
less intensive procedure is to consider not a band but rather a collection of
error bars based on bootstrapping. This method is based on a pointwise
bootstrap approximation to the distribution of
times. A computationally
less intensive procedure is to consider not a band but rather a collection of
error bars based on bootstrapping. This method is based on a pointwise
bootstrap approximation to the distribution of
![]() . In the
following I describe the approach taken by Härdle and Marron (1988), which
uses the wild bootstrap technique to construct pointwise confidence intervals.
How can these pointwise confidence intervals be modified in order to cover the
true curve
. In the
following I describe the approach taken by Härdle and Marron (1988), which
uses the wild bootstrap technique to construct pointwise confidence intervals.
How can these pointwise confidence intervals be modified in order to cover the
true curve ![]() with simultaneous coverage probability
with simultaneous coverage probability ![]() ?
?
A straightforward way of extending bootstrap pointwise intervals to ![]() simultaneous confidence intervals is by applying the Bonferroni method. A
drawback to the Bonferroni approach is that the resulting intervals will quite
often be too long. The reason is that this method does not make use of the
substantial positive correlation of the curve estimates at nearby points.
simultaneous confidence intervals is by applying the Bonferroni method. A
drawback to the Bonferroni approach is that the resulting intervals will quite
often be too long. The reason is that this method does not make use of the
substantial positive correlation of the curve estimates at nearby points.
A more direct approach to finding simultaneous error bars is to consider the
simultaneous coverage on pointwise error bars, and then adjust the pointwise
level to give a simultaneous coverage probability of ![]() . Fisher (1987,
p. 394) called this a ``confidence ribbon'' since the pointwise confidence
intervals are extended until they have the desired simultaneous coverage
probability of
. Fisher (1987,
p. 394) called this a ``confidence ribbon'' since the pointwise confidence
intervals are extended until they have the desired simultaneous coverage
probability of ![]() . A general framework, which includes both the
Bonferroni and direct methods, can be formulated by thinking in terms of
groups of grid points.
. A general framework, which includes both the
Bonferroni and direct methods, can be formulated by thinking in terms of
groups of grid points.
First, partition into ![]() groups as in the Hall and Titterington approach, the
set of locations where error bars are to be computed. Suppose the groups are
indexed by
groups as in the Hall and Titterington approach, the
set of locations where error bars are to be computed. Suppose the groups are
indexed by ![]() and the locations within each group are denoted by
and the locations within each group are denoted by
![]() . The groups should be chosen so that for each
. The groups should be chosen so that for each ![]() the
the ![]() values in each group are within
values in each group are within ![]() of each other. In the
one-dimensional case this is easily accomplished by dividing the
of each other. In the
one-dimensional case this is easily accomplished by dividing the ![]() axis into
intervals of length roughly
axis into
intervals of length roughly ![]() .
.
In order to define a bootstrap procedure that takes advantage of this positive
correlation consider a set of grid points ![]() ,
,
![]() that
have the same asymptotic location
that
have the same asymptotic location ![]() (not depending on
(not depending on ![]() ) relative to
some reference point
) relative to
some reference point ![]() in each group
in each group ![]() . Define
. Define
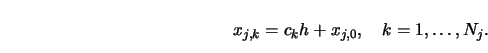
Now, within each group ![]() use the wild bootstrap replications to approximate
the joint distribution of
use the wild bootstrap replications to approximate
the joint distribution of
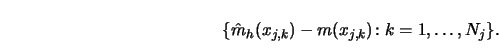
Recall Theorem 4.2.2 for the wild bootstrap approximation to this
distribution. There is was shown that
![\begin{displaymath}\sqrt{n h} [{\hat{m}}_h(x)-m(x)]\end{displaymath}](anrhtmlimg1167.gif)
![\begin{displaymath}\sqrt{n h}[{\hat{m}}_h^*(x)-{\hat{m}}_g(x)]\end{displaymath}](anrhtmlimg1211.gif)
For each ![]() ,
,
![]() , define the interval
, define the interval
![]() to have endpoints which are the
to have endpoints which are the ![]() and the
and the ![]() quantiles of the
quantiles of the
![]() distribution. Then define
distribution. Then define
![]() to be the empirical simultaneous size of the
to be the empirical simultaneous size of the ![]() confidence intervals, that is, the proportion of curves which lie outside at
least one of the intervals in the group
confidence intervals, that is, the proportion of curves which lie outside at
least one of the intervals in the group ![]() . Next find the value of
. Next find the value of ![]() ,
denoted by
,
denoted by ![]() , which makes
, which makes
![]() . The resulting
. The resulting
![]() intervals within each group
intervals within each group ![]() will then have confidence
coefficient
will then have confidence
coefficient ![]() . Hence, by the Bonferroni bound the entire collection
of intervals
. Hence, by the Bonferroni bound the entire collection
of intervals
![]() ,
,
![]() ,
, ![]() , will
simultaneously contain at least
, will
simultaneously contain at least ![]() of the distribution of
of the distribution of
![]() about
about
![]() . Thus the intervals
. Thus the intervals
![]() will be simultaneous
confidence intervals with confidence coefficient at least
will be simultaneous
confidence intervals with confidence coefficient at least ![]() . The
result of this process is summarized as the following theorem.
. The
result of this process is summarized as the following theorem.
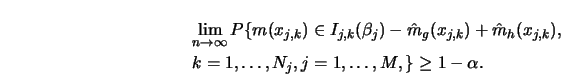
As a practical method for finding ![]() for each group
for each group ![]() we suggest the
following ``halving'' approach.
In particular, first try
we suggest the
following ``halving'' approach.
In particular, first try
![]() ,
and calculate
,
and calculate ![]() . If the result is more than
. If the result is more than ![]() , then try
, then try
![]() , otherwise next try
, otherwise next try
![]() . Continue this
halving approach until neighboring (since only finitely many bootstrap
replications are made, there is only a finite grid of possible
. Continue this
halving approach until neighboring (since only finitely many bootstrap
replications are made, there is only a finite grid of possible ![]() s
available) values
s
available) values ![]() and
and ![]() are found so that
are found so that
![]() .
Finally, take a weighted average
of the
.
Finally, take a weighted average
of the ![]() and the
and the ![]() intervals where the weights are
intervals where the weights are
![]() and
and
![]() ,
respectively.
,
respectively.
Note that Theorem 4.3.2 contains, as a special case, the asymptotic validity
of both the Bonferroni and the direct simultaneous error bars. Bonferroni is
the special case
![]() , and the direct method is where
, and the direct method is where ![]() .
.
The wild bootstrap simultaneous error bars are constructed according to the following algorithm.
REPEAT
b=b+1
STEP 1.
Sample ![]() from the two-point distribution
from the two-point distribution ![]() 4.2.9, where
4.2.9, where

STEP 2.
Construct wild bootstrap observations

UNTIL b=B=number of bootstrap samples.
STEP 3.
Calculate
![]() as follows.
as follows.
First try
![]() , and calculate
, and calculate ![]() .
.
If the result is more than ![]() , then try
, then try
![]() , otherwise
next try
, otherwise
next try
![]() .
.
Continue this halving approach until neighboring values ![]() and
and
![]() are found so that
are found so that
![]() .
.
Finally, take a weighted average of the ![]() and the
and the ![]() intervals
where the weights are
intervals
where the weights are


Define
![\begin{displaymath}[C L O^*(x_{j,k}), CUP^*(x_{j,k})]={\hat{m}}_h(x_{j,k})-
{\hat{m}}_g(x_{j,k})+I_{j,k}(\beta_j).\end{displaymath}](anrhtmlimg1238.gif)
STEP 4.
Draw the interval
![]() around
around
![]() at the
at the
![]() distinct points
distinct points
![]() .
.
This wild bootstrap technique was applied to the potato versus net income example. Figure 4.7 displays the error bars for this data.
![\includegraphics[scale=0.2]{ANR4,7.ps}](anrhtmlimg1240.gif)
|
To study the practical difference between the various types of error bars,
Härdle and Marron (1988) considered the distribution of
![]() at
a grid of
at
a grid of ![]() values for some specific examples. They chose the underlying
curve to be of linear form, with an added bell shaped hump,
values for some specific examples. They chose the underlying
curve to be of linear form, with an added bell shaped hump,

![\includegraphics[scale=0.7]{ANR200obs.ps}](anrhtmlimg1248.gif)
|
The marginal distribution of ![]() is
is ![]() , and the conditional distribution
of
, and the conditional distribution
of ![]() is
is
![]() , for
, for
![]() . For each of
these four distributions 200 observations were generated. Figure
4.8 shows
one realization from each of the four settings. Figure 4.8 also shows
. For each of
these four distributions 200 observations were generated. Figure
4.8 shows
one realization from each of the four settings. Figure 4.8 also shows
![]() , as calculated from the crosses, for each setting, together
with a plot of the kernel function at the bottom which shows the effective
amount of local averaging being done in each case. The bandwidth for these
is
, as calculated from the crosses, for each setting, together
with a plot of the kernel function at the bottom which shows the effective
amount of local averaging being done in each case. The bandwidth for these
is ![]() , the optimal bandwidth as in Härdle and Marron (1985b), where the
weight function
, the optimal bandwidth as in Härdle and Marron (1985b), where the
weight function ![]() in that paper was taken to be the indicator function of
in that paper was taken to be the indicator function of
![]() . As expected, more smoothing is required when the error variance is
larger.
. As expected, more smoothing is required when the error variance is
larger.
To study the differences among the various error bars, for each setting, 500
pseudo data sets were generated. Then kernel estimates were calculated, at the
points
![]() using a standard normal density as
kernel. The bandwidth was chosen to be
using a standard normal density as
kernel. The bandwidth was chosen to be ![]() . Figure 4.9
shows, for the
. Figure 4.9
shows, for the ![]() distribution,
distribution, ![]() overlayed with error bars whose
endpoints are various types of quantiles of the distribution of
overlayed with error bars whose
endpoints are various types of quantiles of the distribution of
![]() .
The centers of the error bars are at the means of these distributions, and
show clearly the bias that is inherent in nonparametric regression estimation.
Note, in particular, how substantial bias is caused by both the curvature of
.
The centers of the error bars are at the means of these distributions, and
show clearly the bias that is inherent in nonparametric regression estimation.
Note, in particular, how substantial bias is caused by both the curvature of
![]() near the hump, and by the curvature of
near the hump, and by the curvature of ![]() near
near ![]() . The bars
in Figure 4.9a are 80% pointwise error bars. In Figure
4.9b they are 80%
simultaneous bars. In Figure 4.9c, the
. The bars
in Figure 4.9a are 80% pointwise error bars. In Figure
4.9b they are 80%
simultaneous bars. In Figure 4.9c, the ![]() values were split up into the
neighborhoods
values were split up into the
neighborhoods
![]() ,
,
![]() ,
,
![]() ,
,
![]() and the neighborhood method of Theorem
4.3.2 was used.
Figure 4.9d shows the completely Bonferroni 80% error bars.
and the neighborhood method of Theorem
4.3.2 was used.
Figure 4.9d shows the completely Bonferroni 80% error bars.
![\includegraphics[scale=0.2]{ANR4,9a.ps}](anrhtmlimg1259.gif) ![\includegraphics[scale=0.2]{ANR4,9b.ps}](anrhtmlimg1260.gif)
|
For easy comparison of the lengths of these intervals, consider Figure
4.10.
This shows, for the same ![]() values, the lengths of the various bars in Figure
4.9. Of course, these bars are shorter near the center, which reflects the
fact that there is more data there, so the estimates are more accurate. As
expected, the lengths increase from pointwise, to actual simultaneous, to
neighborhood, to Bonferroni bars. Also note that, as stated above, the
difference between the actual simultaneous bars and the neighborhood
simultaneous bars is really quite small, whereas the pointwise bars are a lot
narrower.
values, the lengths of the various bars in Figure
4.9. Of course, these bars are shorter near the center, which reflects the
fact that there is more data there, so the estimates are more accurate. As
expected, the lengths increase from pointwise, to actual simultaneous, to
neighborhood, to Bonferroni bars. Also note that, as stated above, the
difference between the actual simultaneous bars and the neighborhood
simultaneous bars is really quite small, whereas the pointwise bars are a lot
narrower.
![\includegraphics[scale=0.2]{ANR4,10.ps}](anrhtmlimg1261.gif)
|
Exercises
4.3.1 Refine Algorithm 4.3.2 to allow a kernel with ![]() .
.
4.3.2 Use the WARPing algorithm of Exercise 4.2.3 on the wild bootstrap smoothing to program Algorithm 4.3.4 for simultaneous error bars.
4.3.3 Compare the naive bootstrap bands with the wild bootstrap error bars. Where do you see the essential difference?
[Hint: Consider the bias of
![]() .]
.]
4.3.4 Use Algorithm 4.3.2 to find a smooth uniform confidence band for the motorcycle data set.
4.3.5 Could you translate Theorem 4.3.1 into the world of ![]() -
-![]() smoothing using the equivalence statements of Section 3.11?
smoothing using the equivalence statements of Section 3.11?
An important issue is how to fine tune the choice of the pilot bandwidth ![]() .
Though it is true that the bootstrap works (in the sense of giving
asymptotically correct coverage probabilities) with a rather crude choice of
.
Though it is true that the bootstrap works (in the sense of giving
asymptotically correct coverage probabilities) with a rather crude choice of
![]() , it is intuitively clear that specification of
, it is intuitively clear that specification of ![]() will play a role in how
well it works for finite samples. Since the main role of the pilot smooth is
to provide a correct adjustment for the bias, we use the goal of bias
estimation as a criterion. We think theoretical analysis of the above type
will be more straightforward than allowing the
will play a role in how
well it works for finite samples. Since the main role of the pilot smooth is
to provide a correct adjustment for the bias, we use the goal of bias
estimation as a criterion. We think theoretical analysis of the above type
will be more straightforward than allowing the ![]() to increase, which
provides further motivation for considering this general grouping framework.
to increase, which
provides further motivation for considering this general grouping framework.
In particular, recall that the bias in the estimation of ![]() by
by
![]() is given by
is given by
![\begin{displaymath}b_h(x)=E^{Y \vert X}[{\hat{m}}_h(x)]-m(x).\end{displaymath}](anrhtmlimg1264.gif)
![\begin{eqnarray*}
{\hat{b}}_{h,g}(x)&=&E^*[{\hat{m}}_h^*(x)]-{\hat{m}}_g(x)\cr
...
...1}^n K_h (x-X_i) {\hat{m}}_g(X_i)/{\hat{f}}_h(x)-{\hat{m}}_g(x).
\end{eqnarray*}](anrhtmlimg1265.gif)
![\begin{displaymath}E[({\hat{b}}_{h,g}(x)-b_h(x))^2 \vert X_1,\ldots,X_n] \sim h^4[C_1 n^{-1}g^{-
5}+C_2 g^4],\end{displaymath}](anrhtmlimg1268.gif)
![\begin{eqnarray*}
C_1&=&\int(K'')^2 {1 \over 2} d_K \sigma^2 (x)/f(x),\cr
C_2&=&({1 \over 2} d_K)^4 [(m f)^{(4)}-(m f'')'']^2 (x)/f(x)^2.
\end{eqnarray*}](anrhtmlimg1269.gif)
An immediate consequence of Theorem 4.3.3 is that the rate of convergence of ![]() for
for ![]() should be
should be ![]() . This makes precise the above intuition
which indicated that
. This makes precise the above intuition
which indicated that ![]() should be slightly oversmoothed. In addition, under
these assumptions reasonable choices of
should be slightly oversmoothed. In addition, under
these assumptions reasonable choices of ![]() will be of the order
will be of the order ![]() .
Hence, Theorem 4.3.3 shows once again that
.
Hence, Theorem 4.3.3 shows once again that ![]() should tend to zero more slowly
than
should tend to zero more slowly
than ![]() . A proof of Theorem 4.3.3 is contained in Härdle and
Marron (1988).
. A proof of Theorem 4.3.3 is contained in Härdle and
Marron (1988).