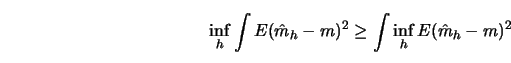
A smoothing parameter that is selected by one of the
previously described methods optimizes a global error criterion.
Such a ``global" choice need not necessarily be optimal
for the estimation of the regression curve at one particular point,
as the trivial inequality
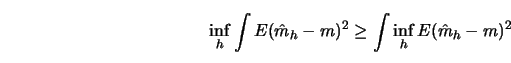
We have already seen that the so-called wild bootstrap method (Section
4.2)
allows us to approximate the distribution
of
![]() . In the following, though, I would like to
present a slightly different bootstrap method in the simpler setting of
i.i.d. error terms. This simpler setting has the advantage that resampling
can be done from the whole set of observed residuals.
Let
. In the following, though, I would like to
present a slightly different bootstrap method in the simpler setting of
i.i.d. error terms. This simpler setting has the advantage that resampling
can be done from the whole set of observed residuals.
Let ![]() and
and
![]() .
The stochastics of the
observations are completely determined by the observation error.
Resampling should therefore be performed with the estimated residuals,
.
The stochastics of the
observations are completely determined by the observation error.
Resampling should therefore be performed with the estimated residuals,
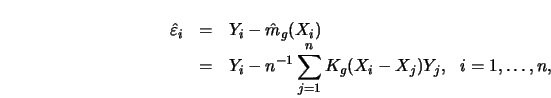



In the bootstrap, any occurrence of ![]() is replaced by
is replaced by
![]() , and therefore
, and therefore
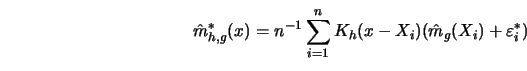
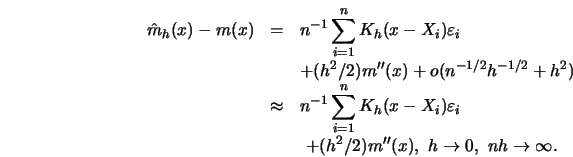
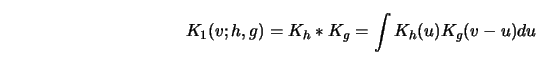
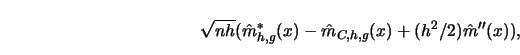
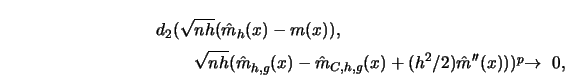
![\begin{displaymath}d_2(F,G)=\inf_{{X \sim F}\atop{Y \sim G}} [ E_{(X,Y)} (X-Y)^2 ]^{1/2}\end{displaymath}](anrhtmlimg1724.gif)
The MSE
![]() can then be estimated by
can then be estimated by
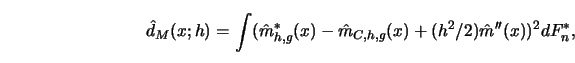
This choice of
local adaptive bandwidth is asymptotically optimal in the sense of
Theorem 5.1.1 as Härdle and Bowman (1988) show; that is,
This adaptive choice of ![]() is illustrated in Figure
5.15, which displays some data simulated by adding a normally distributed
error, with standard deviation 0.1, to the curve
is illustrated in Figure
5.15, which displays some data simulated by adding a normally distributed
error, with standard deviation 0.1, to the curve
![]() evaluated at
evaluated at
![]() ,
,
![]() .
Cross-validation was used to select a good global smoothing parameter
.
Cross-validation was used to select a good global smoothing parameter
![]() and the resulting estimate of the regression function shows
the problems caused by bias at the peaks and troughs, where
and the resulting estimate of the regression function shows
the problems caused by bias at the peaks and troughs, where
![]() is high.
is high.
![\includegraphics[scale=0.12]{ANR5,13.ps}](anrhtmlimg1740.gif)
|
To see what local smoothing parameters have been actually used
consider Figure 5.16. This figure plots the local smoothing
parameters obtained by minimizing the bootstrap estimate ![]() as
a function of
as
a function of ![]() .
.
![\includegraphics[scale=0.12]{ANR5,14.ps}](anrhtmlimg1742.gif)
|
For comparison, the asymptotically optimal local smoothing parameters

![\begin{displaymath}C_0(x)=\left[ {\sigma^2 \ c_K \over
d_K \ m''(x))^2 } \right]^{1/5}, \end{displaymath}](anrhtmlimg1744.gif)
The so-called supersmoother proposed by Friedman (1984) is based
on local linear ![]() -
-![]() fits in a variable
neighborhood of the estimation point
fits in a variable
neighborhood of the estimation point
![]() . ``Local cross-validation" is applied
to estimate the optimal span
as a function of the predictor variable. The algorithm is based
on the
. ``Local cross-validation" is applied
to estimate the optimal span
as a function of the predictor variable. The algorithm is based
on the ![]() updating formulas as described in Section 3.4.
It is therefore highly computationally efficient.
updating formulas as described in Section 3.4.
It is therefore highly computationally efficient.
The name ``supersmoother"
stems from the fact that it uses optimizing resampling techniques at a
minimum of computational effort.
The basic idea of the supersmoother is the same as that for the bootstrap
smoother. Both methods attempt to minimize
the local mean squared error. The supersmoother is constructed from three
initial smooths, the tweeter, midrange and woofer. They are
intended to reproduce the three main parts of the frequency spectrum of
![]() and are defined by
and are defined by ![]() -
-![]() smooths with
smooths with ![]() ,
, ![]() and
and ![]() ,
respectively. Next, the cross-validated residuals
,
respectively. Next, the cross-validated residuals
Since a smooth based on this span sequence would, in
practice, have an unnecessarily high variance, smoothing
the values
![]() against
against ![]() is recommended
using the resulting
smooth to select the best span values,
is recommended
using the resulting
smooth to select the best span values, ![]() . In a further step
the span
values
. In a further step
the span
values ![]() are smoothed against
are smoothed against ![]() (with a midrange smoother). The
result is an estimated span for each observation with a value between the
tweeter and the woofer values.
(with a midrange smoother). The
result is an estimated span for each observation with a value between the
tweeter and the woofer values.
The resulting curve estimate,
the supersmoother, is obtained by interpolating between the two (out of
the three) smoothers with closest span values.
Figure 5.17 shows ![]() pairs
pairs
![]() with
with ![]() uniform on
uniform on ![]() ,
,
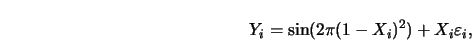
![\includegraphics[scale=0.7]{ANRsupsmo.ps}](anrhtmlimg1760.gif)
|
Figure 5.18 shows the estimated optimal span ![]() as a function
of
as a function
of ![]() .
In the ``low-noise high-curvature" region
.
In the ``low-noise high-curvature" region ![]() the tweeter span is
proposed. In the remaining regions a span value about the midrange is
suggested.
the tweeter span is
proposed. In the remaining regions a span value about the midrange is
suggested.
![\includegraphics[scale=0.2]{ANR5,16.ps}](anrhtmlimg1763.gif)
|
When ![]() is very smooth, more accurate curve estimates can
be obtained by biasing the smoothing parameter toward larger span values.
One way of doing this would be to use a smoothing parameter selection
criterion that penalizes more than the ``no smoothing" point
is very smooth, more accurate curve estimates can
be obtained by biasing the smoothing parameter toward larger span values.
One way of doing this would be to use a smoothing parameter selection
criterion that penalizes more than the ``no smoothing" point ![]() . For
example, Rice's
. For
example, Rice's ![]() (Figure 5.10) would bias the estimator toward
smoother curves. Friedman (1984) proposed parameterizing this ``selection
bias" for enhancing the bass component of the smoother output. For this
purpose, introduce the span
(Figure 5.10) would bias the estimator toward
smoother curves. Friedman (1984) proposed parameterizing this ``selection
bias" for enhancing the bass component of the smoother output. For this
purpose, introduce the span
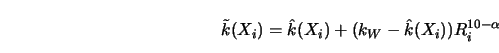
![\begin{displaymath}R_i = \left[ {\hat e (X_i, \hat k (X_i)) \over \hat e (X_i, k_W)} \right],
\end{displaymath}](anrhtmlimg1765.gif)
Exercises
5.3.1Prove that the term
![]() is an approximation of lower order
than
is an approximation of lower order
than ![]() to
to
![]() ,
,
5.3.2What is the difference between the method here in Section 5.3 and the wild bootstrap? Can you prove Theorem 5.3.1 without the bias estimate?
[Hint: Use an oversmooth resampling mean ![]() to construct the
boostrap observations,
to construct the
boostrap observations,
![]() . The
difference
. The
difference

5.3.3Show that the cross-validated residuals 5.3.18 stem from the
leave-out technique applied to ![]() -
-![]() smoothing.
smoothing.
5.3.4Try the woofer, midrange and tweeter on the simulated data set from Table 2, Appendix. Compare it with the supersmoother. Can you comment on where and why the supersmoother changed the smoothing parameter?
[Hint: Use XploRe (1989) or a similar interactive package.]