5.2 Which selector should be used?

There are a number of different automatic selectors that produce asymptotically optimal kernel smoothers. Certainly, any such bandwidth selector is desirable but there may be data sets where a specific selector may outperform other candidates. This raises the question of which selector to use and how far a specific automatic bandwidth is from its optimum. A further interesting question is how close the deviations $d_\bullet(\cdot)$, evaluated at the asymptotically optimal bandwidth, are from the smallest possible deviations. The answers to these questions are surprising. All presented selectors are equivalent in an asymptotic sense. The speed at which an estimated bandwidth tends to the best possible bandwidth is extremely slow. In addition, theoretical studies show that the optimally data-driven bandwidth is negatively correlated with the best possible theoretical bandwidth.

Unfortunately, the mathematics necessary to investigate this issue are rather complicated so I prefer to work in the fixed design model with equispaced design variables on the unit interval, that is, $\{ X_i=i/n\}_{i=1}^n$. Assume further that the $\varepsilon_i$ have common variance, $\sigma^2$, say. The kernel estimator proposed by Priestley and Chao (1972) is considered,

$$\hat m_h(x)=n^{-1}\ \sum_{i=1}^n K_h(x-X_i)\ Y_i.$$

Extensions to random $X$-values and the case of a multivariate $X$-variate are possible but require substantially more work. The optimal bandwidth is taken here in this section to be $\hat h_0$, the minimizer of the average square error (ASE),

$$d_A(h)=n^{-1}\ \sum_{i=1}^n ( \hat m_h(X_i)-m(X_i) )^2 \ w(X_i).$$

Of course, this is just one way to define an optimal bandwidth. An asymptotically equivalent measure of accuracy is the mean average square error (see Theorem 4.1.1)

$$MASE = d_{MA}(h)=E d_A(h) .$$

Another good candidate for a selected bandwidth could therefore be $h_0$, the minimizer of $d_{MA}$. The optimal bandwidth $\hat h_0$ makes $\hat m_h$ as close as possible to the regression curve $m$ for the data set at hand, whereas $h_0$ tries to optimize an average distance over all possible data sets.

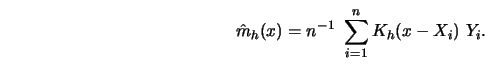
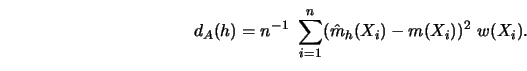
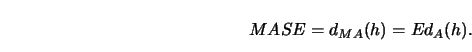
How fast do $\hat h_0$ and $h_0$ tend to zero? We have seen that $\hat h_0$ and $h_0$ are each roughly equal to

$$h_0^*=C_0\ n^{-1/5},$$

where

$$C_0=\left\{ {\sigma^2 \ (\int w(u)du)\ c_K \over d_K \ \int (m''(u))^2 w(u)du } \right\}^{1/5}\cdotp$$ (5.2.10)

Of course, we can try to estimate $C_0$ by the plug-in method, but there may be a difference when using cross-validation or the penalizing function approach. In this setting of equidistant $X_i$ on the unit interval, the penalizing functions that are presented in Section 5.1 can be written as

$$G(h)=p(h)\ \Xi \ (n^{-1}h^{-1}),$$

where

$$p(h)=n^{-1}\ \sum_{i=1}^n ( Y_i-\hat m_h(X_i) )^2 \ w(X_i)$$

denotes the prediction error and where $\Xi$ denotes the penalizing function that corrects the biasedness of $p(h)$ as an estimator for $d_A(h)$.

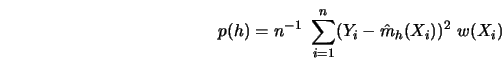
Simple examples are:

(i)

Generalized Cross-validation (Craven and Whaba 1979; Li 1985),

$$\Xi_{GCV} \ (n^{-1}h^{-1})=(1-n^{-1}h^{-1}K(0))^{-2};$$

(ii)

Akaike's Information Criterion (Akaike 1970)

$$\Xi_{AIC}(n^{-1}h^{-1})=\exp\ (2n^{-1}h^{-1}K(0));$$

(iii)

Finite Prediction Error (Akaike 1974),

$$\Xi_{FPE}(n^{-1}h^{-1})=(1+n^{-1}h^{-1}K(0))/ (1-n^{-1}h^{-1}K(0));$$

(iv)

Shibata's (1981) model selector,

$$\Xi_S(n^{-1}h^{-1})=1+2n^{-1}h^{-1}K(0);$$

(v)

Rice's (1984a) bandwidth selector,

$$\Xi_T(n^{-1}h^{-1})=(1-2n^{-1}h^{-1}K(0))^{-1}.$$

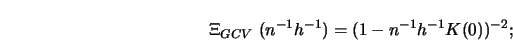
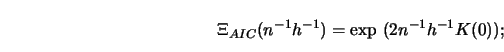
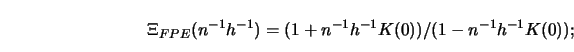
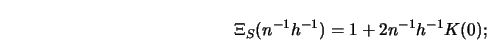
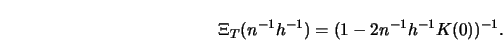
To gain some insight into how these selection functions differ from each other, consider Figure 5.10.

Figure 5.10: Plot of five different correction functions $\Xi(n^{-1}h^{-1}K(0))$ as a function of $h$. The sample size was assumed to be $n=75$ and the Epanechnikov kernel with $K(0)=0.75$ was used. ANRpenalize.xpl

Each of the displayed penalizing functions has the same Taylor expansion, more precisely, as $nh \to \infty$,

$$\Xi \ (n^{-1}h^{-1})=1+2n^{-1}h^{-1}K(0)+O(n^{-2}h^{-2}).$$

The main difference among the $\Xi$-functions occurs at the left tail, where small bandwidths are differently penalized. Note also that the cross-validation method can be seen as penalizing the prediction error $p(h)$, since

$$CV(h)/p(h)=1+2n^{-1}h^{-1}K(0)+O_p(n^{-2}h^{-2}).$$ (5.2.11)

This last statement can be shown to hold also for bandwidth selectors based on unbiased risk estimation,

$$\tilde R(h)=n^{-1}\ \sum_{i=1}^n \{ (Y_i-\hat m_h(X_i))^2+n^{-1}h^{-1}K(0)\ (Y_i-Y_{i-1})^2\} \ w(X_i);$$

see Rice (1984a).

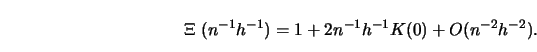
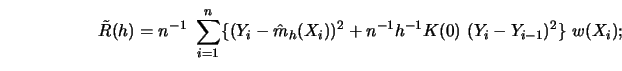
All the above bandwidth selectors are asymptotically optimal, that is, the ratio of estimated loss to minimum loss tends to one,

$${d_A (\hat h) \over d_A (\hat h_0)} {\buildrel p \over \to} 1,$$ (5.2.12)

and the ratio of bandwidths tends to one,

$${\hat h \over \hat h_0} {\buildrel p \over \to} 1.$$ (5.2.13)

The question of how fast this convergence in 5.2.12 and 5.2.13 occurs is answered by computing the asymptotic distributions of the difference.

Theorem 5.2.1   Suppose that

30pt to 30pt(A1) the errors $\{ \varepsilon_i \}$ are independent and identically distributed with mean zero, variance $\sigma^2$, and all other moments finite;

30pt to 30pt(A2) the kernel K is compactly supported with a Hölder continuous second derivative;

30pt to 30pt(A3) the regression function $m$ has a uniformly continuous integrable second derivative.

Then, as $n \to \infty,$

$$n^{3/10} ( \hat h - \hat h_0 ) \ {\buildrel {\cal L}\over \to } \ N(0,\sigma^2_1),$$ (5.2.14)

$$n ( d_A (\hat h) - d_A (\hat h_0)) \ {\buildrel {\cal L}\over \to } \ C_1 \chi^2_1,$$

where $\sigma_1$ and $C_1$ are constants depending on the kernel, the regression function and the observation error, but not on the specific $\Xi$-function that has been selected.

Precise formula for $\sigma_1$ and $C_1$ are given subsequently. A proof of this theorem may be found in Härdle, Hall and Marron (1988).

Between $\hat h$ and $\hat h_0$, the above convergence speeds 5.2.14 are saying that the relative difference

$${ \hat h - \hat h_0 \over \hat h_0 },$$

decreases at the (slow) rate $n^{-1/10}$. Also

$${ d_A (\hat h) - d_A (\hat h_0) \over d_A (\hat h_0)}$$

has the (slow) rate $n^{1/5}$. Of course, in practical research the speed of $\hat h$ is not of interest per se. The researcher cares more about the precision of the curve measured in $d_A(\hat h)$. However, both these rates seem at first glance to be extremely disappointing, but they are of the same order as the differences between $\hat h_0$ and $h_0$ and $d_A (h_0) - d_A (\hat h_0)$.

Theorem 5.2.2   Suppose that $(A1)-(A3)$ in Theorem 5.2.1 hold, then

$$n^{3/10} ( h_0 - \hat h_0 ) \ {\buildrel {\cal L}\over \to} \ N(0, \sigma^2_2),$$

$$n [ d_A (h_0) - d_A (\hat h_0) ] \ {\buildrel {\cal L}\over \to} \ C_2 \chi^2_1,$$ (5.2.15)

where $\sigma^2_2$ and $C_2$ are defined in what follows.

The constants $\sigma_1, \sigma_2, C_1, C_2$ from the above two Theorems are

$$\begin{eqnarray*} \sigma^2_1 &=& \sigma^2_4 /C^2_3,\cr \sigma^2_2 &= &\sigma^2_3... ...3, \cr C_1 &=& C_3 \sigma^2_1 /2, \cr C_2 &=& C_3 \sigma^2_2 /2, \end{eqnarray*}$$

where (letting $\ast$ denote convolution)

$$\begin{eqnarray*} \sigma^2_4&=& {8 \over {C^3_0}} \sigma^4 \left[ \int w^2 \righ... ...[ \int w \right] + 3C^2_0 d_K^2 \left[ \int (m'')^2w^2 \right] .\end{eqnarray*}$$

An important consequence of these two limit theorems describing the behavior of automatically selected bandwidths is that they imply that the ``plug-in" method of choosing $h$ (in which one substitutes estimates of the unknown parts of $d_{MA}$), even if one knew the unknowns $\sigma^2$ and $\int (m'')^2 w$, has an algebraic rate of convergence no better than that of the $\hat h$s given in Algorithm 5.1.1. Hence the additional noise involved in estimating these unknown parts in practice, especially the second derivative part in the case where $m$ is not very smooth, casts some doubt on the applicability of the plug-in estimator.

By comparing $\sigma^2_1$ and $\sigma^2_2$, the asymptotic variances of the previous two theorems, one sees that $\sigma^2_2\leq \sigma^2_1,$ so $h_0$ is closer to $\hat h_0$ than $\hat h$ is in terms of asymptotic variances. It is important to note that the asymptotic variance $\sigma^2_1$ is independent of the particular correction function $\Xi (n^{-1} h^{-1}),$ although simulation studies to be mentioned subsequently seem to indicate a different performance for different $\Xi$s. In the related field of density estimation Hall and Marron (1987) showed that the relative rate of convergence of

$${ \hat h - \hat h_0 \over \hat h_0 }$$

cannot be improved upon $n^{-1/10}$. This suggests that also in the present setting there is no better estimator $\hat h$ for $\hat h_0$. This issue is further pursued in the Complements to this section.

Several extensions of the above limit theorems are possible. For instance, the assumption that the errors are identically distributed can be relaxed to assuming that $\varepsilon_i$ has variance $\sigma^2(X_i)$, where the variance function $\sigma ^2(x)$ is a smooth function. Also the design points need not be univariate. In the multivariate case with the $X_i$ having dimension $d$, the exponents of the first parts of 5.2.14 and 5.2.15 change from $3/10$ to $(d+2)/ (2(d+4))$.

The kernel $K$ can also be allowed to take on negative values to exploit possible higher rates of convergence (Section 4.1). In particular, if $K$ is of order $(0,p)$ (see Section 4.5) and if $m$ has a uniformly continuous $p$th derivative, then the exponents of convergence change from $3/10$ to $3/ (2(2p+1))$. This says that the relative speed of convergence for estimated bandwidths is slower for functions $m$ with higher derivatives than it is for functions with lower derivatives. One should look not only at the bandwidth limit theorems but also at the limit result for $d_A$. In the case in which $m$ has higher derivatives, $d_A$ converges faster to zero, specifically, at the rate $n^{-2p/ (2p+1 )}$. However, this issue seems to be counter-intuitive. Why is the relative speed for $\hat h$ for higher order kernels slower than that for lower order kernels? To get some insight into this consider the following figure showing $d_{MA}(\cdot)$ for higher and lower order kernels.

Figure 5.11: A sketch of $d_{MA}(\cdot )$ for a higher order $(p=4)$ and a lower order $(p=2)$ kernel for $d=1$.

One can see that $d_{MA}(\cdot)$ for the higher order kernel has a flatter minimum than that the lower order kernel. Therefore, it is harder to approximate the true bandwidth. But since the minimum value $n^{-8/9}$ is smaller than the minimum value $n^{-4/5}$ for the lower order kernel it does not matter so much to miss the minimum $\hat h_0$!

Rice (1984a) and Härdle, Hall and Marron (1988) performed a simulation study in order to shed some light on the finite sample performance of the different selectors. One hundred samples of $n=75$ pseudo-random normal variables, $\varepsilon_i$, with mean zero and standard deviation $\sigma =0.0015$ were generated. These were added to the curve $m(x)= x^3(1-x)^3,$ which allows ``wrap-around-estimation" to eliminate boundary effects. The kernel function was taken to be a rescaled quartic kernel

$$K(u)=(15/8)(1-4u^2)^2 I(\left\vert u \right\vert \le 1/2).$$

The result of these simulation studies can be qualitativly described as follows. The selectors have been compared using the number of times out of 100 Monte Carlo repetitions that either the ratio of MASE

$$d_{MA}(\hat h)/d_{MA}(h_0)$$

or the ratio of ASE

$$d_A(\hat h)/d_A(\hat h_0)$$

exceeded $1.05, 1.1, \ldots$ and so on. The $T$ selector turned out to be the best in these simulations. To understand this better, consider the form of the selectors more closely. All these selectors have a trivial minimum at $h=n^{-1} K(0)=0.025,$ the ``no smoothing" point where $\hat m_h (X_i)=Y_i$. The prediction error $p(h)$ has a second-order zero at the ``no smoothing" point. $GCV$ counters this by using a correction factor which has a double pole there, as does $T$. On the other hand, $FPE$ has only a single pole, while $AIC$ and $S$ have no poles at the ``no smoothing" point.

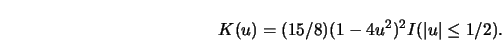
The ordering of performance that was observed in both studies can be qualitatively described through the number of poles that a selector had at the ``no smoothing" point. The more poles the penalizing function had the better it was in these studies.

Figure 5.12 gives an indication of what the limit theorems actually mean in terms of the actual curves, for one of the actual curves and for one of the 100 data sets (with $\sigma=0.011$ and $n=75$). The solid curve in each plot is $m(x)$. The dashed curves are the estimates $\hat m_h(x)$.

Figure 5.12: Plot of $n=75$ regression observations simulated from solid curve $m(x)= x^3(1-x)^3$ and kernel smooth (quartic kernel) with $h=0.26$. From Härdle, Hall and Marron (1988) with permission of the American Statistical Association. ANR75regobs.xpl

Figure 5.13: Plot of $n=75$ regression observations simulated from solid curve $m(x)= x^3(1-x)^3$ and kernel smooth (quartic kernel) with $h=0.39$. From Härdle, Hall and Marron (1988) with permission of the American Statistical Association. ANR75regobs.xpl

Figure 5.14: Plot of $n=75$ regression observations simulated from solid curve $m(x)= x^3(1-x)^3$ and kernel smooth (quartic kernel) with $h=0.66$. From Härdle, Hall and Marron (1988) with permission of the American Statistical Association. ANR74regobs.xpl

In Figure 5.12 the dashed curve is computed with $\hat h=.26,$ the minimizer of $S$ for that data set. In Figure 5.13, $\hat m_h$ is computed with $h=.39$, the minimizer of ASE. Finally in Figure 5.14 the curve suggested by all the other selectors $(h=.66)$ is shown. This example of how different the selectors can be for a specific data set was chosen to demonstrate again the slow rate of convergence in the above limit theorems. More details about this study, for example, the question of how close to normality the distribution of $n^{3/10} (\hat h- \hat h_0)$ is, for this small sample size, can be found in Härdle, Hall and Marron (1988).

Table 5.1 shows the sample mean and standard deviation of the bandwidth minimizing the quantity listed at the left. It is interesting that the selector whose mean matches best with $\hat h_0$ is the rather poorly performing $FPE$, which is not surprising given the comments on the poles above. The selector $T$ biases slightly toward $\hat h$, while $FPE$ biases more downwards. The last two columns show the sample correlation coefficients for the selected bandwidth with $\hat h_0$ and $\hat h_{GCV}$, the minimizer of $GCV$, respectively.

Table 5.1: Summary statistics for automatically chosen and optimal bandwidths from 100 data sets

$\hat{h}$	$\mu_{n}(\hat{h})$	$\sigma_{n}(\hat{h})$	$\rho_{n}(\hat{h},\hat{h_{0}})$	$\rho_{n}(\hat{h},\hat{h_{GCV}})$
		$n=75$
ASE	.51000	.10507	1.00000	-.46002
T	.56035	.13845	-.50654	.85076
CV	.57287	.15411	-.47494	.87105
GCV	.52929	.16510	-.46602	1.00000
R	.52482	.17852	-.40540	.83565
FPE	.49790	.17846	-.45879	.76829
AIC	.49379	.18169	-.46472	.76597
S	.39435	.21350	-.21965	.52915
		$n=500$
ASE	.36010	.07198	1.00000	-.31463
T	.32740	.08558	-.32243	.99869
GCV	.32580	.08864	-.31463	1.00000
AIC	.32200	.08865	-.30113	.97373
S	.31840	.08886	-.29687	.97308

Source:From Härdle, Hall and Marron (1988) with permission of the American Statistical Association.

The simulations shown in Table 5.1. indicated that, despite the equivalence of all selectors, Rice's $T$ had a slightly better performance. This stemmed, as explained, from the fact that the selector $T$ has a slight bias towards oversmoothing (pole of $T$ at twice the ``no smoothing" point). The performance of $T$ should get worse if the simulation setting is changed in such a way that ``reduction of bias is more important than reduction of variance". With other words the right branch of the $d_A(h)$ curve becomes steeper than the left.

A simulation study in this direction was carried out by Härdle (1986e). The sample was constructed from $n=75$ observations with normal errors, $\sigma=0.05$, and a sinusoidal regression curve $m(x)=\sin(\lambda 2\pi x)$. The quartic kernel was chosen. The number of exceedances (formulated as above) for $\lambda =1, 2, 3$ was studied.

As expected, the performance of $T$ got worse as $\lambda$ increased, which supports the hypothesis that the relatively good performance of $T$ was due to the specific simulation setting. The best overall performance, though, showed GCV (generalized cross-validation).

Exercises

5.2.1Prove that in the setting of this section the cross-validation function approach is also based on a penalizing idea, that is, prove formula (5.2.2)

$$CV(h)/p(h)=1+2n^{-1}h^{-1}K(0)+O_p(n^{-2}h^{-2}).$$

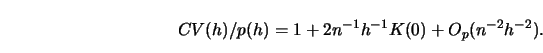
5.2.2Show that $\tilde R(h)$, the unbiased risk estimation selection function, satisfies

$$\tilde R(h)/p(h)=1+2n^{-1}h^{-1}K(0)+o_p(n^{-1}h^{-1}).$$

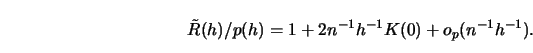
5.2.3Interpret the penalizing term for a uniform kernel using the fact that $N = 2nh$ points fall into a kernel neighborhood. What does ``penalizing" now mean in terms of $N$?

5.2.4Prove that from the relative convergence 5.2.12

$${d_A (\hat h) \over d_A (\hat h_0)} {\buildrel p \over \to} 1$$

it follows that the ratio of bandwidths tends to one, that is,

$${\hat h \over \hat h_0} {\buildrel p \over \to} 1.$$

[Hint : Use Theorem 4.1.1 and Taylor expansion.]

5.2.5Recall the variances of Theorem 5.2.1 and 5.2.2. Show that

$$\sigma_2^2 \le \sigma_1^2.$$

[Hint : Use the Cauchy-Schwarz inequality.]

5.2.6Can you construct a confidence interval for the bandwidths $\hat h_0$?

5.2.7Can you construct a confidence interval for the distance $d_A (\hat h_0)$?

5.2.8How would you extend Theorem 5.2.1 and 5.2.2 to the random design setting.

[Hint : Look at Härdle, Hall and Marron (1990) and use the linearization of the kernel smoother as in Section 4.2]

5.2.1 Complements

I have mentioned that in the related field of density estimation there is a lower-bound result by Hall and Marron (1987) which shows that

$${ \hat h - \hat h_0 \over \hat h_0 }$$

cannot be smaller than $n^{-1/10}$. A natural question to ask is whether this relative difference can be made smaller when $\hat h_0$ is replaced by $h_0$, the minimizer of MISE. In the paper by Hall and Marron (1988) it is argued that this relative difference can be made as small as $n^{-1/2}$. This looks like a drastic improvement, but as Mammen (1988) shows, the search for such bandwidths is not justified. In particular, he shows

Theorem 5.2.3   Suppose that there exists a data-based bandwidth $\hat h$ with

$${ \hat h - h_0 \over h_0 } = o_p(n^{-1/10}).$$

Then there exists another data-based bandwidth $\tilde h$ such that

$$n( d_I(\tilde h) - d_I(\hat h_0)) {\buildrel {\cal L}\over \to} \ \gamma_1 \chi^2_1,$$

$$n( d_I(\hat h) - d_I(\hat h_0) ) {\buildrel {\cal L}\over \to} \ \gamma_2 \chi^2_1,$$

with $0 < \gamma_1 < \gamma_2$.

This theorem suggests that

$${ E( d_I(\tilde h)) - E (d_I(\hat h_0)) \over E( d_I(\hat h)) - E( d_I(\hat h_0)) }$$

converges to a constant, which is strictly smaller than one. Clearly $d_I(\tilde h) \ge d_I(\hat h_0)$ and $d_I(\hat h) \ge d_I(\hat h_0)$. Therefore, this would imply that using the bandwidth $\tilde h$ leads to a smaller risk than using $\hat h$. For more details see Mammen (1988).