As regards problems of specification, these are entirely a matter
for the practical statistician, for those cases where the qualitative nature
of the hypothetical population is known do not involve any problems of this
type.
Sir R. A. Fisher (1922)
A regression curve describes a general relationship between an
explanatory variable ![]() and a response variable
and a response variable ![]() . Having observed
. Having observed ![]() , the
average value of
, the
average value of ![]() is given by the regression function. It is of great
interest to have some knowledge about this relation. The form of the
regression function may tell us where higher
is given by the regression function. It is of great
interest to have some knowledge about this relation. The form of the
regression function may tell us where higher ![]() -observations are to be
expected for certain values of
-observations are to be
expected for certain values of ![]() or whether a special sort of dependence
between the two variables is indicated. Interesting special features are, for
instance, monotonicity or unimodality. Other characteristics include the
location of zeros or the size of extrema. Also, quite often the regression
curve itself is not the target of interest but rather derivatives of it or
other functionals.
or whether a special sort of dependence
between the two variables is indicated. Interesting special features are, for
instance, monotonicity or unimodality. Other characteristics include the
location of zeros or the size of extrema. Also, quite often the regression
curve itself is not the target of interest but rather derivatives of it or
other functionals.
If ![]() data points
data points
![]() have been collected, the regression
relationship can be modeled as
have been collected, the regression
relationship can be modeled as
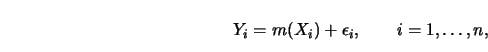
![\includegraphics[scale=0.7]{ANRpotasun.ps}](anrhtmlimg132.gif)
|
In this particular situation one is interested in estimating the mean
expenditure as a function of income. The main body of the data covers only a
quarter of the diagram with a bad ``signal to ink
ratio''(Tufte; 1983) : it
seems therefore to be difficult to determine the average expenditure for given
income ![]() . The aim of a
regression analysis is to produce a reasonable
analysis to the unknown response function
. The aim of a
regression analysis is to produce a reasonable
analysis to the unknown response function ![]() . By reducing the
observational errors it allows interpretation to concentrate on important
details of the mean dependence of
. By reducing the
observational errors it allows interpretation to concentrate on important
details of the mean dependence of ![]() on
on ![]() . This curve approximation
procedure is commonly called ``smoothing''.
. This curve approximation
procedure is commonly called ``smoothing''.
This task of approximating the mean function can be done essentially in two
ways. The quite often used parametric approach is to assume that the
mean curve ![]() has some prespecified functional form, for example, a line with
unknown slope and intercept. As an alternative one could try to estimate
has some prespecified functional form, for example, a line with
unknown slope and intercept. As an alternative one could try to estimate ![]() nonparametrically without reference to a specific form. The first
approach to analyze a regression relationship is called parametric since it is
assumed that the functional form is fully described by a finite set of
parameters. A typical example of a parametric model is a polynomial regression
equation where the parameters are the coefficients of the independent
variables. A tacit assumption of the parametric approach though is that the
curve can be represented in terms of the parametric model or that, at least,
it is believed that the approximation bias of the best parametric fit is a
negligible quantity.
By contrast, nonparametric modeling of a regression
relationship does not project the observed data into a Procrustean bed of a
fixed parametrization, for example, fit a line to the potato data. A preselected
parametric model might be too restricted or too low-dimensional to fit
unexpected features, whereas thenonparametric smoothing approach offers a
flexible tool in analyzing unknown regression relationships.
nonparametrically without reference to a specific form. The first
approach to analyze a regression relationship is called parametric since it is
assumed that the functional form is fully described by a finite set of
parameters. A typical example of a parametric model is a polynomial regression
equation where the parameters are the coefficients of the independent
variables. A tacit assumption of the parametric approach though is that the
curve can be represented in terms of the parametric model or that, at least,
it is believed that the approximation bias of the best parametric fit is a
negligible quantity.
By contrast, nonparametric modeling of a regression
relationship does not project the observed data into a Procrustean bed of a
fixed parametrization, for example, fit a line to the potato data. A preselected
parametric model might be too restricted or too low-dimensional to fit
unexpected features, whereas thenonparametric smoothing approach offers a
flexible tool in analyzing unknown regression relationships.
The term nonparametric thus refers to the flexible functional form of the regression curve. There are other notions of ``nonparametric statistics'' which refer mostly to distribution-free methods. In the present context, however, neither the error distribution nor the functional form of the mean function is prespecified.
The question of which approach should be taken in data analysis was a key issue in a bitter fight between Pearson and Fisher in the twenties. Fisher pointed out that the nonparametric approach gave generally poor efficiency whereas Pearson was more concerned about the specification question. Tapia and Thompson (1978) summarize this discussion in the related setting of density estimation.
Fisher neatly side-stepped the question of what to do in case one did not know the functional form of the unknown density. He did this by separating the problem of determining the form of the unknown density (in Fisher's terminology, the problem of ``specification'') from the problem of determining the parameters which characterize a specified density (in Fisher's terminology, the problem of ``estimation'').
Both viewpoints are interesting in their own right. Pearson pointed out that
the price we have to pay for pure parametric fitting is the possibility of
gross misspecification resulting in too high a model bias. On the other hand,
Fisher was concerned about a too pure consideration of parameter-free models
which may result in more variable estimates, especially for small sample size
![]() .
.
An example for these two different approaches is given in Figure reffig:12 where the straight line indicates a linear parametric fit (Leser; 1963, eq. 2a) and the other curve is a nonparametric smoothing estimate. Both curves model the market demand for potatoes as a function of income from the point cloud presented in Figure 1.1 The linear parametric model is unable to represent a decreasing demand for potatoes as a function of increasing income. The nonparametric smoothing approach suggests here rather an approximate U-shaped regression relation between income and expenditure for potatoes. Of course, to make this graphical way of assessing features more precise we need to know how much variability we have to expect when using the nonparametric approach. This is discussed in Chapter 4. Another approach could be to combine the advantages of both methods in a semiparametric mixture. This line of thought is discussed in Chapters 9 and 10.
![\includegraphics[scale=0.7]{ANRpotareg.ps}](anrhtmlimg136.gif)
|