In the last section we have pointed out how resampling can offer additional insights in a data analysis. We now want to discuss applications of bootstrap that are more in the tradition of classical statistics. We will introduce resampling approaches for the construction of confidence intervals and of testing procedures. The majority of the huge amount of the bootstrap literature is devoted to these topics. There exist two basic approaches for the construction of confidence regions:
Approaches based on pivot statistics are classical methods for the
construction of confidence sets. In a statistical model
![]() a pivot statistic is a random
quantity
a pivot statistic is a random
quantity
![]() that depends on the unknown
parameter
that depends on the unknown
parameter ![]() and on the observation (vector)
and on the observation (vector) ![]() and that has
the following property. The distribution of
and that has
the following property. The distribution of ![]() under
under
![]() does not depend on
does not depend on ![]() . Thus the distribution of
. Thus the distribution of ![]() is known
and one can calculate quantiles
is known
and one can calculate quantiles
![]() such that
such that
![]() . Then
. Then
![]() is a confidence set of the unknown
parameter
is a confidence set of the unknown
parameter ![]() with coverage probability
with coverage probability
![]() . Classical examples are i.i.d. normal observations
. Classical examples are i.i.d. normal observations ![]() with mean
with mean ![]() and variance
and variance ![]() . Then
. Then
![]() is a pivot statistic. Here
is a pivot statistic. Here
![]() is the sample
mean and
is the sample
mean and
![]() is
the sample variance. Then we get, e.g.
is
the sample variance. Then we get, e.g.
![]() is a confidence interval for
is a confidence interval for ![]() with
exact coverage probability
with
exact coverage probability ![]() . Here
. Here
![]() is the
is the
![]() quantile of the t-distribution with
quantile of the t-distribution with ![]() degrees of
freedom.
degrees of
freedom.
Pivot statistics only exist in very rare cases. However for a very
rich class of settings one can find statistics
![]() that
have a limiting distribution
that
have a limiting distribution
![]() that smoothly
depends on
that smoothly
depends on ![]() . Such statistics are called asymptotic pivot
statistics. If now
. Such statistics are called asymptotic pivot
statistics. If now
![]() are chosen such that
under
are chosen such that
under
![]() the interval
the interval
![]() has probability
has probability ![]() then we get that
then we get that
![]() converges to
converges to ![]() . Here
. Here
![]() is a consistent estimate of
is a consistent estimate of ![]() and the confidence set
and the confidence set
![]() is defined as above. A standard
example can be easily given if an estimate
is defined as above. A standard
example can be easily given if an estimate
![]() of a
(one-dimensional, say) parameter
of a
(one-dimensional, say) parameter
![]() is given that
is asymptotically normal. Then
is given that
is asymptotically normal. Then
![]() converges in distribution towards a normal limit with mean zero and
variance
converges in distribution towards a normal limit with mean zero and
variance
![]() depending on the unknown parameter
depending on the unknown parameter
![]() . Here
. Here
![]() or the
studentized version
or the
studentized version
![]() with a consistent estimate
with a consistent estimate
![]() of
of ![]() could be used as asymptotic
pivot. Asymptotic pivot
confidence intervals are based on the quantiles of the asymptotic
distribution
could be used as asymptotic
pivot. Asymptotic pivot
confidence intervals are based on the quantiles of the asymptotic
distribution
![]() of
of ![]() . The
bootstrap idea is to simulate the finite sample distribution
. The
bootstrap idea is to simulate the finite sample distribution
![]() of the pivot statistic
of the pivot statistic ![]() instead of using
the asymptotic distribution of
instead of using
the asymptotic distribution of ![]() . This distribution depends on
. This distribution depends on ![]() and on the unknown parameter
and on the unknown parameter ![]() . The
bootstrap idea is to estimate the unknown parameter and to plug it in.
Then
bootstrap quantiles for
. The
bootstrap idea is to estimate the unknown parameter and to plug it in.
Then
bootstrap quantiles for ![]() are defined as the (random) quantiles of
are defined as the (random) quantiles of
![]() . For the unstudentized statistic
. For the unstudentized statistic
![]() we get the
bootstrap confidence interval
we get the
bootstrap confidence interval
![]() where
where
![]() is the
is the ![]() bootstrap quantile and
bootstrap quantile and
![]() is the
is the
![]() bootstrap quantile. This confidence interval has an asymptotic
coverage probability equal to
bootstrap quantile. This confidence interval has an asymptotic
coverage probability equal to ![]() . We want to illustrate this
approach by the data example of the last section. Suppose we fit
a GARCH(1,1) model to the logreturns and we want to have a confidence
interval for
. We want to illustrate this
approach by the data example of the last section. Suppose we fit
a GARCH(1,1) model to the logreturns and we want to have a confidence
interval for
![]() . It is known that
a GARCH(1,1) process is covariance stationary if and only if
. It is known that
a GARCH(1,1) process is covariance stationary if and only if
![]() . For values of
. For values of ![]() that approximate
that approximate ![]() , one gets a very high
persistency of shocks on the process. We now construct
a bootstrap confidence interval for
, one gets a very high
persistency of shocks on the process. We now construct
a bootstrap confidence interval for ![]() . We used
. We used
![]() as asymptotic pivot statistic. The results are
summarized in Table 2.1.
as asymptotic pivot statistic. The results are
summarized in Table 2.1.
We also applied the
GARCH(1,1)
bootstrap to the first half and to the second half of our data set.
The results are summarized in Table 2.2. The value
of
![]() is quite similar for both halves. The fitted
parameter is always contained in the confidence interval based on the
other half of the sample. Both
confidence intervals have a broad overlap. So there seems no reason
to expect different values of
is quite similar for both halves. The fitted
parameter is always contained in the confidence interval based on the
other half of the sample. Both
confidence intervals have a broad overlap. So there seems no reason
to expect different values of ![]() for the two halves of the data.
The situation becomes a little bit confused if we compare
Table 2.2 with Table 2.1. Both fitted values
of
for the two halves of the data.
The situation becomes a little bit confused if we compare
Table 2.2 with Table 2.1. Both fitted values
of ![]() , the value for the first half and for the second half, are
not contained in the confidence interval that is based on the whole
sample. This suggests that
a GARCH(1,1) model with fixed parameters for the whole sample is not
an appropriate model. A model with different values seems to be more
realistic. When for the whole
time series
a GARCH(1,1) model is fitted the change of the parameters in time
forces the persistency parameter
, the value for the first half and for the second half, are
not contained in the confidence interval that is based on the whole
sample. This suggests that
a GARCH(1,1) model with fixed parameters for the whole sample is not
an appropriate model. A model with different values seems to be more
realistic. When for the whole
time series
a GARCH(1,1) model is fitted the change of the parameters in time
forces the persistency parameter ![]() closer to
closer to ![]() and this effect
increases for
GARCH fits over longer periods. We do not want to discuss this point
further here and refer to [61] for
more details.
and this effect
increases for
GARCH fits over longer periods. We do not want to discuss this point
further here and refer to [61] for
more details.
In [19] another approach for
confidence intervals was suggested. It was supposed to use the
bootstrap quantiles of a test statistic directly as bounds of the
bootstrap confidence intervals. In our example then the
estimate
![]() has to be calculated repeatedly for
bootstrap resamples and the
has to be calculated repeatedly for
bootstrap resamples and the ![]() and
and ![]() empirical
quantiles are used as lower and upper bound for the
bootstrap
confidence intervals. It can be easily checked that we then get
empirical
quantiles are used as lower and upper bound for the
bootstrap
confidence intervals. It can be easily checked that we then get
![]() as
bootstrap confidence interval where the quantiles
as
bootstrap confidence interval where the quantiles
![]() and
and
![]() are defined as above, see also [22]. Note that the interval is just
reflected around
are defined as above, see also [22]. Note that the interval is just
reflected around
![]() . The resulting confidence interval for
. The resulting confidence interval for
![]() is shown in Table 2.3. For asymptotic normal test
statistics both
bootstrap
confidence intervals are asymptotically equivalent. Using higher
order Edgeworth expansions it was shown that
bootstrap pivot intervals achieve a higher order level accuracy.
Modifications of percentile intervals have been proposed that achieve
level accuracy of the same order, see [22]. For a recent discussion on
bootstrap
confidence intervals see also [21,18]. In our data example there is only a minor
difference between the two intervals, cf. Tables 2.1
and 2.3. This may be caused by the very large sample size.
is shown in Table 2.3. For asymptotic normal test
statistics both
bootstrap
confidence intervals are asymptotically equivalent. Using higher
order Edgeworth expansions it was shown that
bootstrap pivot intervals achieve a higher order level accuracy.
Modifications of percentile intervals have been proposed that achieve
level accuracy of the same order, see [22]. For a recent discussion on
bootstrap
confidence intervals see also [21,18]. In our data example there is only a minor
difference between the two intervals, cf. Tables 2.1
and 2.3. This may be caused by the very large sample size.
The basic idea of
bootstrap tests is rather simple. Suppose that for a statistical
model
![]() a testing hypothesis
a testing hypothesis
![]() and a test statistic
and a test statistic ![]() is given.
Then
bootstrap is used to calculate critical values for
is given.
Then
bootstrap is used to calculate critical values for ![]() . This can
be done by fitting a model on the hypothesis and by generating
bootstrap resamples under the fitted hypothesis model. The
. This can
be done by fitting a model on the hypothesis and by generating
bootstrap resamples under the fitted hypothesis model. The ![]() quantile of the test statistic in the
bootstrap samples can be used as critical value. The resulting test
is called
a bootstrap test. Alternatively, a testing approach can be based on
the duality of testing procedures and confidence regions. Each
confidence region defines a testing procedure by using the following
rule. A hypothesis is rejected if no hypothesis parameter lies in the
confidence region. We shortly describe this method for
bootstrap
confidence intervals based on an asymptotic pivot statistic, say
quantile of the test statistic in the
bootstrap samples can be used as critical value. The resulting test
is called
a bootstrap test. Alternatively, a testing approach can be based on
the duality of testing procedures and confidence regions. Each
confidence region defines a testing procedure by using the following
rule. A hypothesis is rejected if no hypothesis parameter lies in the
confidence region. We shortly describe this method for
bootstrap
confidence intervals based on an asymptotic pivot statistic, say
![]() , and the hypothesis
, and the hypothesis
![]() .
Bootstrap resamples are generated (in the unrestricted model) and are
used for estimating the
.
Bootstrap resamples are generated (in the unrestricted model) and are
used for estimating the ![]() quantile of
quantile of
![]() by
by
![]() , say. The
bootstrap test rejects the hypothesis, if
, say. The
bootstrap test rejects the hypothesis, if
![]() is larger than
is larger than
![]() . Higher order
performance of
bootstrap tests has been discussed in Hall (1992)[32]. For
a discussion of
bootstrap tests we also refer to Beran (1988), Beran and Ducharme
(1991)[2,4].
. Higher order
performance of
bootstrap tests has been discussed in Hall (1992)[32]. For
a discussion of
bootstrap tests we also refer to Beran (1988), Beran and Ducharme
(1991)[2,4].
We now compare
bootstrap testing with a more classical
resampling approach for testing
(''conditional tests''). There exist some (important) examples
where, for all test statistics,
resampling can be used to achieve a correct level on the whole
hypothesis for finite samples. Such tests are called similar. For
some testing problems
resampling tests turn out to be the only way to get similar tests.
This situation arises when a statistic is available that is sufficient
on the hypothesis
![]() . Then, by
definition of sufficiency, the conditional distribution of the data
set given this statistic is fixed on the hypothesis and does not
depend on the parameter of the underlying distribution as long as the
parameter lies on the hypothesis. Furthermore, because this
distribution is unique and thus known, resamples can be drawn from
this conditional distribution. The
resampling test then has correct level on the whole hypothesis. We
will now give a more formal description.
. Then, by
definition of sufficiency, the conditional distribution of the data
set given this statistic is fixed on the hypothesis and does not
depend on the parameter of the underlying distribution as long as the
parameter lies on the hypothesis. Furthermore, because this
distribution is unique and thus known, resamples can be drawn from
this conditional distribution. The
resampling test then has correct level on the whole hypothesis. We
will now give a more formal description.
A test ![]() for a vector
for a vector ![]() of observations is called similar if
of observations is called similar if
![]() for all
for all
![]() , where
, where
![]() is the set of parameters on the null hypotheses. We
suppose that a statistic
is the set of parameters on the null hypotheses. We
suppose that a statistic ![]() is available that is sufficient on the
hypothesis. Let
is available that is sufficient on the
hypothesis. Let
![]() be the family of distributions of
be the family of distributions of ![]() on the hypothesis. Then the
conditional distribution of
on the hypothesis. Then the
conditional distribution of ![]() given
given ![]() does not depend on the
underlying parameter
does not depend on the
underlying parameter
![]() because
because ![]() is sufficient.
In particular,
is sufficient.
In particular,
![]() does not depend on
does not depend on ![]() . Then any
test satisfying
. Then any
test satisfying
For a given test statistic ![]() similar tests can be constructed by
choosing
similar tests can be constructed by
choosing
![]() such that
such that
We will consider two examples of
conditional tests. The first one are
permutation tests. For a sample of observations
![]() the order statistic
the order statistic
![]() containing the
ordered sample values
containing the
ordered sample values
![]() is sufficient
on the hypothesis of i.i.d. observations. Given
is sufficient
on the hypothesis of i.i.d. observations. Given ![]() , the conditional
distribution of
, the conditional
distribution of ![]() is
a random permutation of
is
a random permutation of
![]() . The
resampling scheme is very similar to the nonparametric
bootstrap. In the
resampling,
. The
resampling scheme is very similar to the nonparametric
bootstrap. In the
resampling, ![]() pseudo observations are drawn from the original data
sample. Now this is done without replacement whereas in the
bootstrap scheme this is done with replacement. For a comparison of
bootstrap and
permutation tests see also [41]. Also
for the
subsampling (i.e.
resampling with a resample size that is smaller than the sample size)
both schemes (with and without replacement) have been considered. For
a detailed discussion of the
subsampling without replacement see [72].
pseudo observations are drawn from the original data
sample. Now this is done without replacement whereas in the
bootstrap scheme this is done with replacement. For a comparison of
bootstrap and
permutation tests see also [41]. Also
for the
subsampling (i.e.
resampling with a resample size that is smaller than the sample size)
both schemes (with and without replacement) have been considered. For
a detailed discussion of the
subsampling without replacement see [72].
The second example is a popular approach in the physical literature on
nonlinear
time series analysis. For odd sample size ![]() a series
a series
![]() can be written as
can be written as
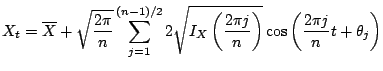 |
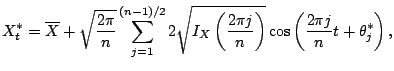 |
We would like to highlight a major difference between
bootstrap and conditional tests.
Bootstrap tests work if they are based on
resampling of an asymptotic pivot statistic. Then the
bootstrap critical values stabilize asymptotically and converge
against the quantile of the limiting distribution of the test
statistic. For conditional tests the situation is quite different.
They work for all test statistics. However, not for all test
statistics it is guaranteed that the critical value
![]() converges to a deterministic limit. In [60] this is discussed for
surrogate data tests. It is shown that also for very large data sets
the surrogate data quantile
converges to a deterministic limit. In [60] this is discussed for
surrogate data tests. It is shown that also for very large data sets
the surrogate data quantile
![]() may have a variance of the
same order as the test statistic
may have a variance of the
same order as the test statistic ![]() . Thus the randomness of
. Thus the randomness of
![]() may change the nature of a test. This is illustrated
by a test statistic for kurtosis of the observations that is
transformed to a test for circular stationarity.
may change the nature of a test. This is illustrated
by a test statistic for kurtosis of the observations that is
transformed to a test for circular stationarity.