This section includes enough algorithms and results to obtain a basic understanding of the opportunities and issues. Fortunately, there have been a number of readable monographs available for the reader interested in pursuing this subject in depth. In rough chronological order, excluding books primarily dealing with nonparametric regression, the list includes [47,65,25,11,42,10,23,14,37,49,60,44,3], and [48].
The purpose of the next section is to provide a survey of important results without delving into the theoretical underpinnings and details. The references cited above are well-suited for that purpose.
Every algorithm for nonparametric density estimation has one or more design parameters which are called the smoothing parameter(s) or bandwidth(s) of the procedure. The smoothing parameter controls the final appearance of the estimate. For an equally-spaced histogram, the bin width plays the primary role of a smoothing parameter. Of course, the bins may be shifted and the location of the bin edges is controlled by the bin origin, which plays the role of a secondary smoothing parameter. For a kernel estimator, the scale or width of the kernel serves as the smoothing parameter. For an orthogonal series estimator, the number of basis functions serves as the smoothing parameter. The smoothing parameters of a spline estimator also include the location of the knots. Similarly, a histogram with completely flexible bin widths has many more than two smoothing parameters.
As a point estimator of ![]() , [27] proved that every
nonparametric density estimator,
, [27] proved that every
nonparametric density estimator,
![]() is biased. However, it
is usually true that the integral of all of the pointwise biases is
0. Thus mean squared error (MSE) and
integrated mean squared error (IMSE) are the appropriate criteria to optimize the tradeoff between
pointwise/integrated variance and squared bias.
is biased. However, it
is usually true that the integral of all of the pointwise biases is
0. Thus mean squared error (MSE) and
integrated mean squared error (IMSE) are the appropriate criteria to optimize the tradeoff between
pointwise/integrated variance and squared bias.
Nonparametric density estimators always underestimate peaks and overestimate valleys in the true density function. Intuitively, the bias is driven by the degree of curvature in the true density. However, since the bias function is continuous and integrates to 0, there must be a few points where the bias does vanish. In fact, letting the smoothing parameter vary pointwise, there are entire intervals where the bias vanishes, including the difficult-to-estimate tail region. This fact has been studied by [15] and [31]. Since the bias of a kernel estimator does not depend on the sample size, these zero-bias or bias-annihilating estimates have more than a theoretical interest. However, there is much more work required for practical application. Alternatively, in higher dimensions away from peaks and valleys, one can annihilate pointwise bias by balancing directions of positive curvature against directions of negative curvature; see [54]. An even more intriguing idea literally adjusts the raw data points towards peaks and away from valleys to reduce bias; see [6].
The rate of convergence of a nonparametric density estimator to the true density is much slower than in the parametric setting, assuming in the latter case that the correct parametric model is known. If the correct parametric model is not known, then the parametric estimates will converge but the bias will not vanish. The convergence is slower still in high dimensions, a fact which is often referred to as the curse of dimensionality. Estimating the derivative of a density function is even harder than coping with an additional dimension of data.
If the ![]() -th derivative of a density is known to be smooth,
then it is theoretically possible to construct an
order-
-th derivative of a density is known to be smooth,
then it is theoretically possible to construct an
order-![]() nonparametric density estimation algorithm.
The pointwise bias is driven by the
nonparametric density estimation algorithm.
The pointwise bias is driven by the ![]() -th derivative
at
-th derivative
at ![]() ,
,
![]() . However, if
. However, if ![]() ,
then the density estimate will take on negative values for
some points,
,
then the density estimate will take on negative values for
some points, ![]() . It is possible to define higher-order algorithms
which are non-negative, but these estimates do not integrate
to
. It is possible to define higher-order algorithms
which are non-negative, but these estimates do not integrate
to ![]() ; see [52].
Thus higher-order density estimation algorithms violate one of the two conditions
for a true density:
; see [52].
Thus higher-order density estimation algorithms violate one of the two conditions
for a true density: ![]() and
and
![]() .
Of course, there are cases where the first condition is
violated for lower-order estimators. Two such cases include
orthogonal series estimators
([18,62]) and boundary-corrected kernel estimators
([26]).
Note that positive kernel estimators correspond to
.
Of course, there are cases where the first condition is
violated for lower-order estimators. Two such cases include
orthogonal series estimators
([18,62]) and boundary-corrected kernel estimators
([26]).
Note that positive kernel estimators correspond to ![]() .
[57] studied the efficacy of higher-order
procedures and suggested
.
[57] studied the efficacy of higher-order
procedures and suggested ![]() often provided superior
estimates. [37] also studied this question
and found some improvement when
often provided superior
estimates. [37] also studied this question
and found some improvement when ![]() , which must be
traded off against the disadvantages of negative estimates.
, which must be
traded off against the disadvantages of negative estimates.
Picking the best smoothing parameter from data is an important task in practice. If the smoothing parameter is too small, the estimate is too noisy, exhibiting high various and extraneous wiggles. If the smoothing parameter is too large, then the estimate may miss key features due to oversmoothing, washing out small details. Such estimates have low variance but high bias in many regions. In practice, bandwidths that do not differ by more than 10-15% from the optimal bandwidth are usually satisfactory.
A statistician experienced in EDA is likely to
find all estimates informative for bandwidths ranging from undersmoothed to
oversmoothed. With a complicated density function, no single choice
for the bandwidth may properly represent the density for all values
of ![]() . Thus the same bandwidth may result in undersmoothing
for some intervals of
. Thus the same bandwidth may result in undersmoothing
for some intervals of ![]() , oversmoothing in another interval,
and yet near optimal smoothing elsewhere. However, the practical
difficulty of constructing locally adaptive estimators makes
the single-bandwidth case of most importance. Simple transformations
of the data scale can often be an effective strategy
([61]).
This strategy was used with the lipid data
in Fig. 4.1, which were transformed to a
, oversmoothing in another interval,
and yet near optimal smoothing elsewhere. However, the practical
difficulty of constructing locally adaptive estimators makes
the single-bandwidth case of most importance. Simple transformations
of the data scale can often be an effective strategy
([61]).
This strategy was used with the lipid data
in Fig. 4.1, which were transformed to a ![]() scale.
scale.
Consider the ![]()
![]() points shown in frame (b) of Fig. 4.4.
Histograms of these data with various numbers of bins are shown in
Fig. 4.7. With so much data, the oversmoothed histogram
Fig. 4.7a captures the major features, but seems biased
downwards at the peaks. The final frame shows a histogram that is
more useful for finding data anomalies than as a good density
estimate.
points shown in frame (b) of Fig. 4.4.
Histograms of these data with various numbers of bins are shown in
Fig. 4.7. With so much data, the oversmoothed histogram
Fig. 4.7a captures the major features, but seems biased
downwards at the peaks. The final frame shows a histogram that is
more useful for finding data anomalies than as a good density
estimate.
The differences are more apparent with a smaller sample size.
Consider the
![]() -cholesterol levels shown in
Fig. 4.1. Three histograms are shown in Fig. 4.8.
The extra one or two modes are at least suggested in the middle panel,
while the histogram in the first panel only suggests a rather unusual
non-normal appearance. The third panel has many large spurious peaks.
We conclude from these two figures that while an oversmoothed
estimator may have a large error relative to the optimal estimator,
the absolute error may still be reasonably small for very large data
samples.
-cholesterol levels shown in
Fig. 4.1. Three histograms are shown in Fig. 4.8.
The extra one or two modes are at least suggested in the middle panel,
while the histogram in the first panel only suggests a rather unusual
non-normal appearance. The third panel has many large spurious peaks.
We conclude from these two figures that while an oversmoothed
estimator may have a large error relative to the optimal estimator,
the absolute error may still be reasonably small for very large data
samples.
While there is no limit on how complicated a density may be
(for which
![]() may grow without bound), the
converse is not true. [53]
and
[51] show that for a particular scale of
a density (for example, the range, standard deviation, or
interquartile range), there is in fact a lower bound among
continuous densities for the roughness quantity
may grow without bound), the
converse is not true. [53]
and
[51] show that for a particular scale of
a density (for example, the range, standard deviation, or
interquartile range), there is in fact a lower bound among
continuous densities for the roughness quantity
Many details of these ideas may be found in the literature and in the many textbooks available. The following section provides some indication of this research.
The basic results of density estimation are perhaps most easily understood with the ordinary histogram. Thus more time will be spent on the histogram with only an outline of results for more sophisticated and more modern algorithms.
Given an equally spaced mesh ![]() over the entire real line with
over the entire real line with
![]() , the density histogram is given by
, the density histogram is given by
Next consider the bias of
![]() at a fixed point,
at a fixed point, ![]() , which
is located in the
, which
is located in the ![]() -th bin. Note that
-th bin. Note that
![]() . A useful approximation to
the bin probability is
. A useful approximation to
the bin probability is
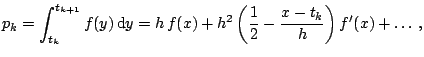 |
(4.4) |
A more complete analysis of the bias ([32]) shows that the integrated squared bias is
approximately
![]() , where
, where
![]() , so that
the IMSE is given by
, so that
the IMSE is given by
Finally, the smoothest density with variance ![]() is
is
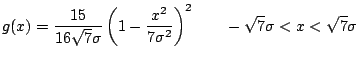 |
(4.8) |
The oversmoothing rule (4.9) may be
inverted when the scale is the range of the density to obtain a lower
bound of
![]() on the number of bins in the optimal
histogram. This formula should be compared to Sturges' rule of
on the number of bins in the optimal
histogram. This formula should be compared to Sturges' rule of
![]() , which is in common use in many statistical
packages ([45]). In fact, the histograms in the first frames of
Figs. 4.7 and 4.8 correspond to Sturges'
rule, while the second frames of these figures correspond to the oversmoothed
bandwidths. Presumably the optimal bandwidth would occur somewhere between
the second and third frames of these figures. Clearly Sturges' rule results
in oversmoothed graphs since the optimal number of bins is severely
underestimated.
, which is in common use in many statistical
packages ([45]). In fact, the histograms in the first frames of
Figs. 4.7 and 4.8 correspond to Sturges'
rule, while the second frames of these figures correspond to the oversmoothed
bandwidths. Presumably the optimal bandwidth would occur somewhere between
the second and third frames of these figures. Clearly Sturges' rule results
in oversmoothed graphs since the optimal number of bins is severely
underestimated.
The histogram is an order-one density estimator, since the bias is determined by the first derivative. The estimators used most in practice are order-two estimators. (Recall that order-three estimators are not non-negative.) Perhaps the most unexpected member of the order-two class is the frequency polygon (FP), which is the piecewise linear interpolant of the midpoints of a histogram. ([33]) showed that
![$\displaystyle \mathrm{IMSE}\, \Bigl[\, \widehat{f}_{\mathrm{FP}} \Bigr] = \frac{2}{3nh} + \frac{49}{2880} h^4 {R}(f^{\prime\prime}) + O\left(n^{-1}\right).$](img3972.gif) |
(4.10) |
The use of wider bins means that the choice of the bin origin
has a larger impact, at least subjectively. Given a set of ![]() shifted
histogram,
shifted
histogram,
![]() , one might use
cross-validation to try to pick the best one. Alternatively,
Scott ([34]) suggested the
averaged shifted histogram (ASH),
which is literally defined:
, one might use
cross-validation to try to pick the best one. Alternatively,
Scott ([34]) suggested the
averaged shifted histogram (ASH),
which is literally defined:
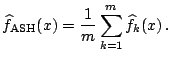 |
(4.11) |
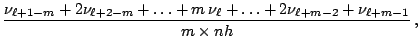 |
(4.12) |
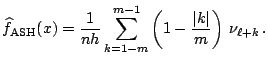 |
(4.13) |
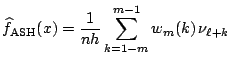 where where |
(4.14) |
In Fig. 4.9, two ASHs of the ![]() -cholesterol data are shown. The bin edge
effects and discontinuities apparent in the ordinary
histogram in Fig. 4.8 are removed. The extra
features in the distribution are hinted at.
-cholesterol data are shown. The bin edge
effects and discontinuities apparent in the ordinary
histogram in Fig. 4.8 are removed. The extra
features in the distribution are hinted at.
The extension of the ASH to bivariate (and multivariate) data
is straightforward. A number of bivariate (multivariate) histograms
are constructed with equal shifts along the coordinate axes and
then averaged together. Figure 4.10 displays a bivariate
ASH of the same lipid data displayed in Fig. 4.1. The strong
bimodal and weak trimodal features are evident. The third mode
is perhaps more clearly represented in a perspective plot;
see Fig. 4.11. (Note that for convenience, the data were rescaled to
the intervals ![]() for these plots, unlike Fig. 4.1.)
The precise location of the third
mode above (and between) the two primary modes results
in the masking of the multiple modes when viewed
along the cholesterol axis alone. This masking feature is
commonplace and a primary reason for trying to extend the
dimensions available for visualization of the density function.
for these plots, unlike Fig. 4.1.)
The precise location of the third
mode above (and between) the two primary modes results
in the masking of the multiple modes when viewed
along the cholesterol axis alone. This masking feature is
commonplace and a primary reason for trying to extend the
dimensions available for visualization of the density function.
The ASH is a discretized representation of a kernel estimator. Binned kernel estimators are of great interest to reduce the computational burden. An alternative to the ASH is the fast Fourier transform approach of [41]. Kernel methods were introduced by [27] and [24] with earlier work by Evelyn Fix and Joe Hodges completed by 1951 in San Antonio, Texas (see [43]).
Given a kernel function, ![]() , which is generally taken to be
a symmetric probability density function, the kernel density estimate is
defined by
, which is generally taken to be
a symmetric probability density function, the kernel density estimate is
defined by
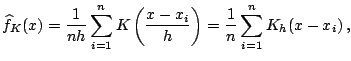 |
(4.15) |
Multivariate extensions of the kernel approach generally rely upon the
product kernel. For example, with bivariate data
![]() , the bivariate (product) kernel estimator is
, the bivariate (product) kernel estimator is
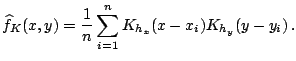 |
(4.16) |
In higher dimensions, some care must be exercised to minimize the
effects of the curse of dimensionality. First, marginal variable
transformations should be explored to avoid a heavily skewed
appearance or heavy tails. Second, a principal components analysis
should be performed to determine if the data are of full rank. If so,
the data should be projected into an appropriate subspace. No
nonparametric procedure works well if the data are not of full rank.
Finally, if the data do not have many significant digits, the data
should be carefully blurred. Otherwise the data may have many
repeated values, and cross-validation algorithms may believe the data
are discrete and suggest using ![]() . Next several kernel or ASH
estimates may be calculated and explored to gain an understanding of
the data, as a preliminary step towards further analyses.
. Next several kernel or ASH
estimates may be calculated and explored to gain an understanding of
the data, as a preliminary step towards further analyses.
An extensive body of work also exists for orthogonal series density estimators. Originally, the Fourier basis was studied, but more modern choices for the basis functions include wavelets. These can be re-expressed as kernel estimators, so we do not pursue these further. In fact, a number of workers have shown how almost any nonparametric density algorithm can be put into the form of a kernel estimator; see [59] and [54], for example. More recent work on local likelihood algorithms for density estimation further shows how closely related parametric and nonparametric thinking really is; see [19] for details and literature.