5.3 Schiefe und Kurtosis

Definition 5.1 (Schiefe)  
Die Schiefe einer Zufallsgröße $X$ mit Erwartungswert $\mu$ und Varianz $\sigma^2$ ist definiert als

$$S(X) = \frac{\mathop{\text{\rm\sf E}}[(X-\mu)^3]}{\sigma^3}.$$

Ist die Schiefe negativ (positiv), so ist die Verteilung linksschief (rechtsschief). Normalverteilte Zufallsgrößen haben eine Schiefe von Null, da die Verteilung symmetrisch um den Erwartungswert ist. Geschätzt wird die Schiefe aus einer Stichprobe von u.i.v. Zufallsgrößen $X_1,\ldots,X_n$ (siehe Abschnitt 3.4) durch

$$\hat{S}(X) = \frac{\frac{1}{n} \sum_{t=1}^n(X_t-\hat{\mu})^3}{\hat{\sigma}^3}$$ (5.2)

wobei $\hat{\mu}, \hat{\sigma}^2$ die im letzten Abschnitt eingeführten Stichprobenmittel und -varianz sind.

Definition 5.2 (Kurtosis)  
Die Kurtosis (oder auch Wölbung) einer Zufallsgröße $X$ mit Erwartungswert $\mu$ und Varianz $\sigma^2$ ist definiert als

   Kurt$$(X) = \frac{\mathop{\text{\rm\sf E}}[(X-\mu)^4]}{\sigma^4}.$$

Normalverteilte Zufallsgrößen haben eine Kurtosis von 3. Eine größere Kurtosis ist bei Finanzdaten oft zu beobachten; dies ist ein Anzeichen dafür, dass Werte nahe bei 0 und vor allem sehr große positive und/oder negative Werte mit im Vergleich zur Normalverteilung hoher Wahrscheinlichkeit auftreten, mittelgroße Werte dagegen seltener. Geschätzt wird die Kurtosis durch

$$\widehat{\mathop{\text{\rm Kurt}}}(X) = \frac{\frac{1}{n} \sum_{t=1}^n(X_t-\hat{\mu})^4}{\hat{\sigma}^4}.$$ (5.3)

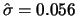
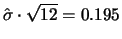
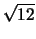
Beispiel 5.1   Die monatlichen DAX Daten von 1979:1 bis 2000:10 haben eine empirische Standardabweichung $\hat{\sigma}=0.056$, entsprechend einer Jahresvolatilität von $\hat{\sigma}\cdot \sqrt{12}=0.195$. Wir kommen in Abschnitt (6.3.4) auf den Faktor $\sqrt{12}$ zurück. Die Kurtosis dieser Daten liegt deutlich über 3 und unterstreicht die Nichtnormalität der DAX Renditen.
SFMsumm.xpl