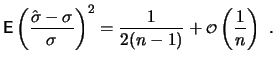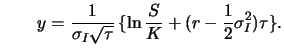Das Handeln mit Optionen ist wegen der starken zufälligen Komponente
mit einem vergleichsweise hohen Risiko verbunden. Fortgeschrittene
Strategien zur Verringerung und Kontrolle dieses Risikos können aus
der Black-Scholes-Formel (6.24) abgeleitet werden. Um die
Problematik zu verdeutlichen, betrachten wir zuerst ein Beispiel und
einige traditionelle Strategien.
Beispiel 8.1
Eine Bank verkauft für 600000 EUR einen europäischen Call
auf 100000 Stück einer dividendenfreien Aktie. Die Parameter
der Option sind in der Tabelle
6.3 dargestellt.
Tabelle 2.7:
Daten des Beispiels
Aktueller Zeitpunkt  |
6 Wochen |
Laufzeit  |
26 Wochen |
Restlaufzeit
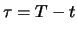 |
20 Wochen = 0.3846 |
stetiger Jahreszinssatz 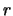 |
0.05 |
Jahresvolatilität der Aktie  |
0.20 |
aktueller Aktienkurs  |
98 EUR |
Ausübungskurs  |
100 EUR |
|
Die Black-Scholes-Formel (
6.24) mit
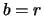
wegen der
Dividendenfreiheit ergibt als Wert der Option 480119 EUR,
also rund 480000 EUR. Die Bank hat die Option um 120000
EUR teurer als ihren theoretischen Wert verkauft, setzt sich
dafür aber dem Risiko von nennenswerten Verlusten aus.
Eine Risikomanagementstrategie ist es, nichts zu tun, d.h. eine ungedeckte Position
(naked position) einzunehmen. Wenn die
Option nach 20 Wochen ausgeübt wird, muss die Bank die Aktie zum
dann aktuellen Kurs kaufen. Steigt der Kurs z.B. auf 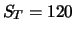 EUR, so kostet dies effektiv
EUR, so kostet dies effektiv
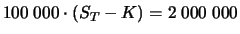 EUR, also deutlich mehr als die durch den Verkauf
der Option erzielten Einnahmen. Steigt andererseits der Kurs nicht
über den Ausübungskurs
EUR, also deutlich mehr als die durch den Verkauf
der Option erzielten Einnahmen. Steigt andererseits der Kurs nicht
über den Ausübungskurs  , so wird die Option nicht
ausgeübt, und die Bank kann 600000 EUR als Gewinn
verbuchen.
, so wird die Option nicht
ausgeübt, und die Bank kann 600000 EUR als Gewinn
verbuchen.
 SFMBSCopt2.xpl
SFMBSCopt2.xpl
Das andere Extrem ist das Einnehmen einer gedeckten Position
(covered position). Sofort nach
dem Verkauf der Option kauft die Bank die bei Ausübung
fälligen Aktien zum Preis von
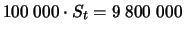 EUR. Wird im Falle
EUR. Wird im Falle 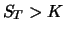 die Option ausgeübt, so werden
die Aktien zum Preis von
die Option ausgeübt, so werden
die Aktien zum Preis von
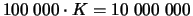 EUR
geliefert. Da dies abgezinst auf den Zeitpunkt
EUR
geliefert. Da dies abgezinst auf den Zeitpunkt  ungefähr dem
ursprünglichen Kaufpreis der Aktien entspricht, beträgt der
Gewinn der Bank in diesem Fall rund 600000 EUR, d.h. dem
für den Verkauf der Option erzielten Betrag. Fällt dagegen der
Aktienkurs auf z.B.
ungefähr dem
ursprünglichen Kaufpreis der Aktien entspricht, beträgt der
Gewinn der Bank in diesem Fall rund 600000 EUR, d.h. dem
für den Verkauf der Option erzielten Betrag. Fällt dagegen der
Aktienkurs auf z.B. 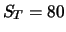 EUR, so wird die Option nicht
ausgeübt. Die Bank verliert aber aus dem Kursverlust der von ihr
gehaltenen Aktien rund 2000000 EUR, also wieder wesentlich
mehr als der für die Option erzielte Erlös. Aus der
Put-Call-Parität für europäische Optionen (Satz 2.3)
folgt übrigens, dass das Risiko aus dem Verkauf eines gedeckten
Calls identisch zum Risiko aus dem Verkauf eines ungedeckten Puts
ist.
EUR, so wird die Option nicht
ausgeübt. Die Bank verliert aber aus dem Kursverlust der von ihr
gehaltenen Aktien rund 2000000 EUR, also wieder wesentlich
mehr als der für die Option erzielte Erlös. Aus der
Put-Call-Parität für europäische Optionen (Satz 2.3)
folgt übrigens, dass das Risiko aus dem Verkauf eines gedeckten
Calls identisch zum Risiko aus dem Verkauf eines ungedeckten Puts
ist.
Beide Risikomanagementstrategien sind unbefriedigend, da die
Kosten sehr stark zwischen 0 und großen Werten variieren. Nach
Black-Scholes entstehen im Mittel Kosten von rund 480000 EUR,
und ein perfekter Hedge sollte dafür sorgen, dass der Einfluss
des Zufalls ausgeschaltet wird und genau diese Kosten entstehen.
Ein aufwendigeres Verfahren zum Hedgen, d.h. zum Beschränken des
Risikos, das mit dem Verkauf eines Calls verbunden ist, ist die
Stop-Loss-Strategie :
Die die Option herausgebende Bank nimmt eine
ungedeckte Position ein, solange der Aktienkurs unterhalb des
Ausübungskurses ist 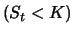 , und wechselt in eine gedeckte
Position, sobald der Call im Geld ist
, und wechselt in eine gedeckte
Position, sobald der Call im Geld ist 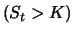 .
.
Die beim Ausüben der Option zu liefernden Aktien werden gekauft,
sobald 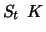 überschreitet, und wieder abgestoßen, sobald
überschreitet, und wieder abgestoßen, sobald  unter
unter  fällt.
fällt.
Da sämtliche Käufe und Verkäufe nach der Zeit 0 zum Kurs  getätigt
wurden, und da bei Fälligkeit
getätigt
wurden, und da bei Fälligkeit  entweder keine Aktien gehalten
werden
entweder keine Aktien gehalten
werden 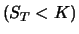 oder sie zum Kurs
oder sie zum Kurs  an den Besitzer des
Calls abgegeben werden
an den Besitzer des
Calls abgegeben werden 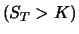 , fallen nach der Zeit 0
nominell keine Kosten an.
, fallen nach der Zeit 0
nominell keine Kosten an.
Kosten entstehen durch diese Hedge-Strategie nur, wenn 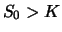 ist,
zur Zeit 0 also Aktien zum Kurs
ist,
zur Zeit 0 also Aktien zum Kurs 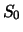 gekauft werden, die später zum
Kurs
gekauft werden, die später zum
Kurs  veräußert werden:
veräußert werden:
Kosten für Stop-Loss-Hedgen:
![$\displaystyle \, \max[S_0 - K,\ 0]. $](sfmimg947.gif)
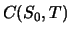 , so dass
Arbitrage durch Verkaufen einer Option und Hedgen mit der
Stop-Loss-Strategie möglich wäre. Bei dieser Argumentation sind aber
mehrere Dinge übersehen worden:
, so dass
Arbitrage durch Verkaufen einer Option und Hedgen mit der
Stop-Loss-Strategie möglich wäre. Bei dieser Argumentation sind aber
mehrere Dinge übersehen worden:
- Kauf und Verkauf der Aktien verursachen
Transaktionskosten,
- durch die Kapitalbindung beim Kauf von Aktien vor der Zeit
 entstehen Zinsverluste,
entstehen Zinsverluste,
- praktisch sind Käufe und Verkäufe zum exakten Kurs
 nicht
möglich; bei steigendem Kurs werden die Aktien für
nicht
möglich; bei steigendem Kurs werden die Aktien für
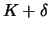 gekauft,
bei fallendem Kurs für
gekauft,
bei fallendem Kurs für 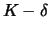 verkauft für ein
verkauft für ein
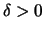 .
.
Praktisch werden Käufe und Verkäufe nur nach jeweils 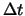 Zeiteinheiten getätigt. Je größer
Zeiteinheiten getätigt. Je größer 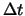 , desto größer ist in der
Regel
, desto größer ist in der
Regel 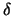 , desto seltener fallen aber die Transaktionskosten an. Hull (2000) hat in einer
Monte Carlo-Studie mit
, desto seltener fallen aber die Transaktionskosten an. Hull (2000) hat in einer
Monte Carlo-Studie mit 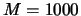 simulierten Kursverläufen untersucht, wie gut sich die Stop-Loss-Strategie als
Verfahren zur Verringerung des Risikos, das mit der Ausgabe einer Kaufoption verbunden ist, eignet.
In jedem Simulationslauf werden die durch Stop-Loss-Verfahren verursachten Kosten
simulierten Kursverläufen untersucht, wie gut sich die Stop-Loss-Strategie als
Verfahren zur Verringerung des Risikos, das mit der Ausgabe einer Kaufoption verbunden ist, eignet.
In jedem Simulationslauf werden die durch Stop-Loss-Verfahren verursachten Kosten
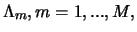 registriert und ihre Stichprobenvarianz
berechnet. Die Größe des nach Anwendung des Stop-Loss-Hedgens verbleibenden Risikos misst
die zur Standardisierung durch den Preis des gehedgten Calls geteilte Stichprobenstandardabweichung
Das Ergebnis zeigt Tabelle 6.4. Ein perfekter Hedge würde das Risiko, d.h. die Variabilität der Kosten,
völlig ausschalten und hätte den Wert
registriert und ihre Stichprobenvarianz
berechnet. Die Größe des nach Anwendung des Stop-Loss-Hedgens verbleibenden Risikos misst
die zur Standardisierung durch den Preis des gehedgten Calls geteilte Stichprobenstandardabweichung
Das Ergebnis zeigt Tabelle 6.4. Ein perfekter Hedge würde das Risiko, d.h. die Variabilität der Kosten,
völlig ausschalten und hätte den Wert 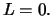
Tabelle 6.4:
Leistung der Stop-Loss-Strategie
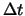 (Wochen) (Wochen) |
5 |
4 |
2 |
1 |
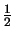 |
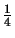 |
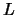 |
1.02 |
0.93 |
0.82 |
0.77 |
0.76 |
0.76 |
|
Zur Begrenzung des Risikos beim Optionshandel werden komplexere
Hedge-Strategien als die bisher betrachteten eingesetzt. Wir
betrachten als Beispiel wieder den Verkauf eines Calls auf
Aktien. Zuerst wird versucht, den Wert des Portfolios über kleine
Zeitintervalle hinweg unempfindlich gegen kleine Schwankungen des
Kurses der der Option zugrunde liegenden Aktie zu machen. Dies nennt
man Delta-Hedgen. Anschließend werden andere der ''Greek
letters'' (Gamma, Theta, Vega, Rho) betrachtet, um die
Feinabstimmung des Hedge-Portfolios zu erreichen.
Unter dem Delta oder der Hedge-Rate einer Kaufoption versteht
man die Ableitung des Optionspreises nach dem
Aktienkurs oder - als diskrete Version - den Differenzenquotienten
der Änderung 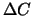 des Optionspreises bei Änderung
des Optionspreises bei Änderung 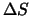 des Aktienkurses:
des Aktienkurses:
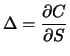
oder
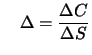
Entsprechend ist das Delta anderer Anlageformen definiert. Die Aktie
selbst hat den Wert 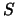 , also
, also
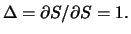 Ein Terminkontrakt auf eine dividendenfreie Aktie hat den Forward
Price
Ein Terminkontrakt auf eine dividendenfreie Aktie hat den Forward
Price
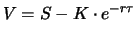 (siehe Satz 2.1) und daher ebenfalls
(siehe Satz 2.1) und daher ebenfalls
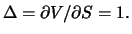 Aktien und Terminkontrakte sind
daher in Delta-Hedge-Portfolios gegeneinander austauschbar. Letztere
werden wegen der niedrigeren Transaktionskosten vorgezogen, wenn sie
verfügbar sind.
Aktien und Terminkontrakte sind
daher in Delta-Hedge-Portfolios gegeneinander austauschbar. Letztere
werden wegen der niedrigeren Transaktionskosten vorgezogen, wenn sie
verfügbar sind.
Beispiel 8.2
Eine Bank verkauft Calls auf 2000
Aktien zum Preis von
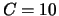
EUR/Aktie bei einem Kurs
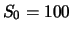
EUR/Aktie. Das Delta des Calls sei
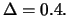
Zum Hedgen werden
die verkauften Calls im Portfolio durch Kauf von
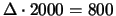
Aktien ergänzt. Kleine Änderungen des Optionswertes werden durch
entsprechende Änderungen des Wertes der Aktien im Portfolio
ausgeglichen. Steigt der Aktienkurs um 1 EUR, d.h. der Wert der Aktien
im Portfolio um 800 EUR, so steigt der Optionswert eines Calls auf 1
Aktie um
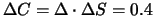
EUR, der Wert aller Calls
im Portfolio also um 800 EUR, was einen Verlust für den Verkäufer des
Calls darstellt. Gewinn und Verlust gleichen sich aus, da das Delta
der Optionsposition durch das Delta der Aktienposition ausgeglichen
wird. Das Gesamtportfolio hat
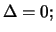
die Bank nimmt eine
deltaneutrale Position ein.
Da das Delta von Optionen u.a. von Aktienkurs und Zeit abhängt,
bleibt eine deltaneutrale Position nur kurzfristig erhalten. In
der Praxis muss beim Delta-Hedgen das Portfolio regelmäßig
den sich ändernden Gegebenheiten angepasst werden. Dies nennt
man Rebalanzieren.
Strategien zum Risikomanagement von Portfolios, die häufiges
Umschichten beinhalten, sind als dynamisches Hedgen
bekannt. Wir merken an, dass die Black-Scholes-Differentialgleichung (6.3) mit Hilfe eines
dynamischen Hedgeportfolios hergeleitet werden kann, dessen Position durch
kontinuierliches Umschichten deltaneutral gehalten wird. Dieser Ansatz ist analog zur Betrachtung
eines die Option duplizierenden Portfolios.
Beispiel 8.3
Der Kurs der dem obigen Call zugrunde liegenden Aktie
steigt innerhalb einer Woche auf 110 EUR. Durch die verstrichene Zeit
und den geänderten Kurs erhöht sich das Delta der Option auf
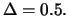
Um erneut eine deltaneutrale Position zu erreichen, müssen
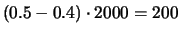
Aktien zum Portfolio hinzugekauft werden.
Aus den Black-Scholes-Formeln für den Wert europäischer Calls und Puts
auf dividendenfreie Aktien ergibt sich als Delta:
wobei 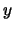 wie in (6.25) definiert ist.
wie in (6.25) definiert ist.
Das Delta (6.27) ist in Abbildung 6.1 als Funktion von
Aktienkurs und Laufzeit dargestellt. Für steigende Aktienkurse geht das Delta
gegen Eins, für fallende gegen Null. Mit anderen Worten, ist die Option sehr weit
im Geld, so wird sie sehr wahrscheinlich am Laufzeitende ausgeübt werden, weshalb man
als Stillhalter dieser Option zur Deckung des Risikos die Aktie (oder einen sehr
großen Teil) halten sollte. Ist die Option andererseits sehr weit aus dem Geld, so wird sie
sehr wahrscheinlich nicht ausgeübt werden, so dass man die Aktie nicht (oder nur einen
kleinen Teil) zu halten braucht.
Abb.:
Das Delta als Funktion von Aktienkurs (rechte Achse) und Laufzeit (linke Achse) mit 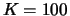 ,
, 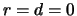 und
und
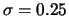 .
.
 SFMdelta.xpl
SFMdelta.xpl
|
|
Weiterhin ist die Wahrscheinlichkeit 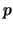 , dass
eine Option aus dem Geld am Laufzeitende
ausgeübt und eine Option im Geld nicht ausgeübt wird größer, je länger die
Laufzeit ist. Das erklärt, weshalb das Delta für längere Laufzeiten flacher (linearer) wird.
, dass
eine Option aus dem Geld am Laufzeitende
ausgeübt und eine Option im Geld nicht ausgeübt wird größer, je länger die
Laufzeit ist. Das erklärt, weshalb das Delta für längere Laufzeiten flacher (linearer) wird.
Tabelle 6.5 nach Hull (2000) zeigt in
derselben Weise wie Tabelle 6.4 für die Stop-Loss-Strategie die
Leistung des Delta-Hedgens in Abhängigkeit von den Abständen 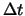 zwischen den Rebalanzierungen des Portfolios. Wenn
zwischen den Rebalanzierungen des Portfolios. Wenn 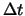 klein genug ist, wird das Risiko aus dem Verkauf des Calls sehr gut
eingegrenzt. Für
klein genug ist, wird das Risiko aus dem Verkauf des Calls sehr gut
eingegrenzt. Für
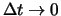 erhält man als Grenzfall die
der Ableitung der Black-Scholes-Formel zugrunde liegende
kontinuierliche Rebalanzierung und die perfekte Ausschaltung des
Risikos
erhält man als Grenzfall die
der Ableitung der Black-Scholes-Formel zugrunde liegende
kontinuierliche Rebalanzierung und die perfekte Ausschaltung des
Risikos 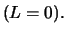
Tabelle 6.5:
Leistung des Delta-Hedgens
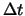 (Wochen) (Wochen) |
5 |
4 |
2 |
1 |
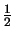 |
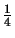 |
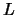 |
0.43 |
0.39 |
0.26 |
0.19 |
0.14 |
0.09 |
|
Wegen der Linearität der Ableitung ist das Delta 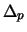 eines
Portfolios, das aus
eines
Portfolios, das aus
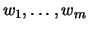 Stück von Derivaten
Stück von Derivaten
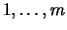 mit Deltas
mit Deltas
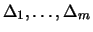 besteht,
einfach:
besteht,
einfach:
Beispiel 8.4
Ein Portfolio aus verschiedenen USD-Optionen besteht aus
- 1.
- 200000 gekauften Calls (long position) mit
Ausübungskurs 1.70 EUR und Fälligkeit in 4 Monaten. Das Delta einer
auf einen einzelnen Dollar bezogenen Option ist
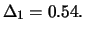
- 2.
- 100000 verkaufte Calls (short position) mit Ausübungskurs
1.75 EUR und Fälligkeit in 6 Monaten mit einem Delta von
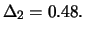
- 3.
- 100000 verkauften Puts (short position) mit Ausübungskurs
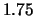 EUR und Fälligkeit in 3 Monaten mit
EUR und Fälligkeit in 3 Monaten mit
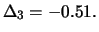
Das Delta des Portfolios ist (Wertsteigerungen verkaufter Optionen
wirken sich negativ auf den Wert des Portfolios aus):
Das Portfolio kann durch Verkauf von 111000 USD oder eines
passenden Terminkontrakts auf USD (beides mit
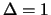
) deltaneutral
gemacht werden.
Beim Delta-Hedgen wird der Optionspreis 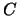 lokal durch eine im
Aktienkurs
lokal durch eine im
Aktienkurs 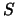 lineare Funktion approximiert. Wenn die Zeit
lineare Funktion approximiert. Wenn die Zeit 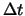 bis zum nächsten Rebalanzieren des Portfolios nicht sehr kurz ist, ist
die Näherung unbefriedigend (vgl. Tabelle 6.5). Daher betrachtet man
eine feinere Approximation, d.h. die Taylor-Entwicklung von
bis zum nächsten Rebalanzieren des Portfolios nicht sehr kurz ist, ist
die Näherung unbefriedigend (vgl. Tabelle 6.5). Daher betrachtet man
eine feinere Approximation, d.h. die Taylor-Entwicklung von 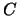 als
Funktion von
als
Funktion von 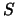 und
und  :
:
Dabei ist (wie wir schon im Beweis
von Satz 6.1 gesehen haben) 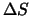 von der
Größenordnung
von der
Größenordnung
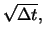 und die in
und die in
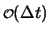 zusammengefassten Terme sind von kleinerer Größenordnung als
zusammengefassten Terme sind von kleinerer Größenordnung als
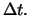 Vernachlässigt man alle Terme bis auf den ersten
(von der Größenordnung
Vernachlässigt man alle Terme bis auf den ersten
(von der Größenordnung
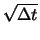 ), so erhält man die dem Delta-Hedgen zugrunde liegende Näherung
Berücksichtigt man auch die Terme der Größenordnung
), so erhält man die dem Delta-Hedgen zugrunde liegende Näherung
Berücksichtigt man auch die Terme der Größenordnung 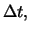 so
folgt
wobei
so
folgt
wobei
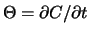 das Theta und
das Theta und
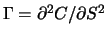 das Gamma der
Option ist.
das Gamma der
Option ist. 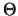 heißt auch Zeitverfall (time decay) der
Option. Für einen dividendenfreien Call erhält man aus der
Black-Scholes-Formel (6.24):
und
heißt auch Zeitverfall (time decay) der
Option. Für einen dividendenfreien Call erhält man aus der
Black-Scholes-Formel (6.24):
und
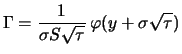 |
(8.28) |
mit dem in (6.25) definierten 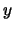 .
.
Das Gamma in (6.28) ist in Abbildung (6.2) geplottet als Funktion von
Aktienkurs und Laufzeit. Optionen, deren Deltas am sensitivsten auf Kursänderungen reagieren, sind
am Geld und haben kurze Laufzeiten. Bei diesen Optionen sind also häufige Umschichtungen erforderlich,
wenn man Delta-Hedgen betreibt.
Abb.:
Das Gamma als Funktion von Aktienkurs (rechte Achse) und Laufzeit (linke Achse), mit 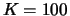 ,
, 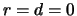 und
und
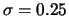 .
.
 SFMgamma.xpl
SFMgamma.xpl
|
|
Beim Gamma-Hedgen geht man von einem
bereits deltaneutralen Portfolio aus und versucht es, durch
Hinzukauf oder Verkauf von Derivaten gammaneutral zu machen, d.h.
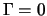 zu erreichen und den Wert des Portfolios noch
stabiler gegen Änderungen des Aktienkurses zu machen. Für das
Gamma-Hedgen kann man allerdings weder Aktien noch Terminkontrakte
benutzen, da beide konstantes
zu erreichen und den Wert des Portfolios noch
stabiler gegen Änderungen des Aktienkurses zu machen. Für das
Gamma-Hedgen kann man allerdings weder Aktien noch Terminkontrakte
benutzen, da beide konstantes 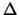 und daher
und daher
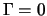 haben. Andererseits ist dies auch von Vorteil, da man diese
Instrumente einsetzen kann, um ein bereits gammaneutrales
Portfolio deltaneutral zu machen, ohne das Gamma zu ändern. Zum
Gamma-Hedgen einer Position aus Optionen mit einem Gammawert
haben. Andererseits ist dies auch von Vorteil, da man diese
Instrumente einsetzen kann, um ein bereits gammaneutrales
Portfolio deltaneutral zu machen, ohne das Gamma zu ändern. Zum
Gamma-Hedgen einer Position aus Optionen mit einem Gammawert
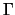 kann man z.B.
kann man z.B. 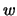 Stück einer in der Börse
gehandelten Option mit einem Gamma von
Stück einer in der Börse
gehandelten Option mit einem Gamma von 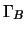 einsetzen. Das
Gamma des Portfolios ist dann
einsetzen. Das
Gamma des Portfolios ist dann
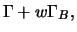 also 0 für
also 0 für
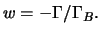
Beispiel 8.5
Ein Portfolio aus USD-Optionen und US-Dollars sei bereits
deltaneutral mit
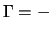
150000. An der Terminbörse wird ein
USD-Call mit
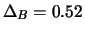
und
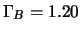
angeboten. Das
Portfolio wird durch Hinzufügen von
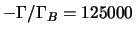
dieser Calls gammaneutral. Sein
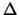
ist danach aber
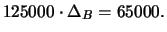
Die Deltaneutralität kann z.B. durch Verkauf von
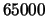
USD aus dem Portfolio wiedergestellt werden, ohne das Gamma zu
ändern.
Im Gegensatz zur Entwicklung des Aktienkurses ist der Ablauf der
Zeit deterministisch und mit keinen risikosteigernden
Unwägbarkeiten verbunden. Wenn 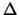 und
und 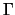 beide 0
sind, so ändert sich der Wert der Option (näherungsweise)
risikofrei mit der Rate
beide 0
sind, so ändert sich der Wert der Option (näherungsweise)
risikofrei mit der Rate
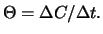 Der
Parameter
Der
Parameter 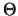 ist für die meisten Optionen negativ; eine
Option verliert an Wert, je näher der Fälligkeitsterm rückt.
ist für die meisten Optionen negativ; eine
Option verliert an Wert, je näher der Fälligkeitsterm rückt.
Aus der Black-Scholes-Gleichung (6.24) folgt für ein deltaneutrales
Portfolio aus Aktienoptionen
wobei 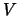 der Wert des Portfolios ist.
der Wert des Portfolios ist. 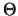 und
und 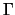 hängen
auf einfache Weise voneinander ab, so dass
hängen
auf einfache Weise voneinander ab, so dass 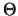 anstelle von
anstelle von
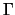 zum Gamma-Hedgen eines deltaneutralen Portfolios benutzt
werden kann.
zum Gamma-Hedgen eines deltaneutralen Portfolios benutzt
werden kann.
Der Black-Scholes-Ansatz geht davon aus, dass die Volatilität  konstant ist. Das Auftreten von Smiles zeigt, dass diese Annahme in der
Praxis nicht gerechtfertigt ist. Daher kann es sinnvoll sein, den Wert
eines Portfolios auch unempfindlich gegenüber Änderungen der
Volatilität zu machen. Dabei benutzt man das Vega eines
Portfolios (in der Literatur manchmal auch Lambda oder Kappa genannt),
das für z.B. einen Call definiert ist als
konstant ist. Das Auftreten von Smiles zeigt, dass diese Annahme in der
Praxis nicht gerechtfertigt ist. Daher kann es sinnvoll sein, den Wert
eines Portfolios auch unempfindlich gegenüber Änderungen der
Volatilität zu machen. Dabei benutzt man das Vega eines
Portfolios (in der Literatur manchmal auch Lambda oder Kappa genannt),
das für z.B. einen Call definiert ist als
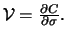
Aktien und Terminkontrakte haben
 so dass man beim
Vega-Hedgen wieder auf an der Börse gehandelte Optionen zurückgreifen
muss. Da ein veganeutrales Portfolio nicht automatisch gammaneutral
ist, muss man beim Hedgen zwei verschiedene Optionen einsetzen, um
gleichzeitig
so dass man beim
Vega-Hedgen wieder auf an der Börse gehandelte Optionen zurückgreifen
muss. Da ein veganeutrales Portfolio nicht automatisch gammaneutral
ist, muss man beim Hedgen zwei verschiedene Optionen einsetzen, um
gleichzeitig
 und
und
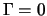 zu erreichen.
zu erreichen.
Aus der Black-Scholes-Formel (6.24) mit dem dort definierten 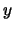 ergibt
sich als Vega eines Calls auf eine dividendenfreie Aktie
ergibt
sich als Vega eines Calls auf eine dividendenfreie Aktie
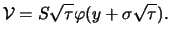 |
(8.29) |
Da die Black-Scholes-Formel unter der Annahme konstanter Volatilität
hergeleitet worden ist, ist es eigentlich nicht gerechtfertigt,  durch Ableiten von (6.24) nach
durch Ableiten von (6.24) nach  zu berechnen. Die obige
Formel für
zu berechnen. Die obige
Formel für 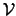 ist aber sehr ähnlich zu einer Gleichung für
ist aber sehr ähnlich zu einer Gleichung für
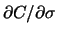 , die aus einem allgemeineren Modell mit
stochastischer Volatilität folgt, so dass sie näherungsweise benutzt
werden kann.
, die aus einem allgemeineren Modell mit
stochastischer Volatilität folgt, so dass sie näherungsweise benutzt
werden kann.
Das Vega in (6.29) ist in Abbildung 6.3 dargestellt als Funktion des
Aktienkurses und der Laufzeit. Optionen am Geld mit langer Laufzeit reagieren am sensitivsten
auf Änderungen der Volatilität.
Abb.:
Das Vega als Funktion von Aktienkurs (rechte Achse) und Laufzeit (linke
Achse), mit 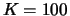 ,
, 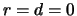 und
und
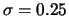 .
.
 SFMvega.xpl
SFMvega.xpl
|
|
Schließlich kann man das mit einem Call verbundene Risiko aufgrund von
Zinsschwankungen begrenzen, indem man das Rho der Option zum
Hedgen benutzt:
Für einen Call auf eine dividendenfreie Aktie ergibt sich aus (6.24)
Bei Währungsoptionen müssen dabei neben den inländischen auch die
Zinsschwankungen im Land der Fremdwährung berücksichtigt werden, so
dass beim Rho-Hedgen zwei verschiedene Werte
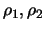 betrachtet werden.
betrachtet werden.
In den Black-Scholes-Formeln (6.22), (6.24) sind alle
Optionsparameter bekannt mit Ausnahme der Volatilität 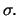 In der Praxis schätzt man
In der Praxis schätzt man  aus vorhandenen
Beobachtungen des Aktienkurses oder der an der Börse notierten
Preise ähnlicher Optionen.
aus vorhandenen
Beobachtungen des Aktienkurses oder der an der Börse notierten
Preise ähnlicher Optionen.
Die historische Volatilität (historic
volatility) ist ein Schätzer
für  auf der Grundlage des Schwankungsverhaltens der
Aktie in der Vergangenheit. Sind z.B.
auf der Grundlage des Schwankungsverhaltens der
Aktie in der Vergangenheit. Sind z.B.
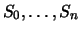 die
Aktienkurse zu den Zeitpunkten
die
Aktienkurse zu den Zeitpunkten
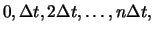 so sind die logarithmierten relativen Zuwächse
so sind die logarithmierten relativen Zuwächse
unabhängige identisch normalverteilte Zufallsgrößen, wenn man den Kurs
 als geometrische Brownsche Bewegung modelliert.
als geometrische Brownsche Bewegung modelliert. 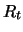 ist der
Zuwachs
ist der
Zuwachs
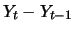 des logarithmierten Aktienkurses
des logarithmierten Aktienkurses
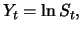 der nach Abschnitt 5.4
ein Wiener-Prozess mit Varianzrate
der nach Abschnitt 5.4
ein Wiener-Prozess mit Varianzrate 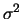 ist, über ein Zeitintervall der Länge
ist, über ein Zeitintervall der Länge 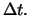 Die
Varianz von
Die
Varianz von 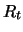 ist daher
Ein guter Schätzer für
ist daher
Ein guter Schätzer für
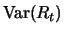 ist die Stichprobenvarianz
wobei
ist die Stichprobenvarianz
wobei
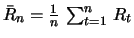 das Stichprobenmittel ist.
das Stichprobenmittel ist.
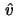 ist erwartungstreu, d.h.
ist erwartungstreu, d.h.
![$ \mathop{\text{\rm\sf E}}[\hat{v}] = v,\ $](sfmimg1045.gif) und die Zufallsgröße
hat eine bekannte Verteilung, eine
und die Zufallsgröße
hat eine bekannte Verteilung, eine
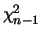 -Verteilung
(Chi-Quadrat mit
-Verteilung
(Chi-Quadrat mit 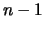 Freiheitsgraden). Daraus folgt insbesondere,
dass der mittlere relative quadratische Schätzfehler von
Freiheitsgraden). Daraus folgt insbesondere,
dass der mittlere relative quadratische Schätzfehler von 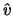 ist. Da
ist. Da
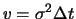 , erhält man auf der Basis der
historischen Aktienkurse
, erhält man auf der Basis der
historischen Aktienkurse
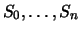 als Schätzer für die
Volatilität
als Schätzer für die
Volatilität  Durch Taylorentwicklung der Wurzel und mit den bekannten Größen
Durch Taylorentwicklung der Wurzel und mit den bekannten Größen
![$ \mathop{\text{\rm\sf E}}[
\hat{v}]$](sfmimg1053.gif) und
und
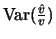 folgt, dass
folgt, dass
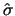 erwartungstreu bis auf Terme der Größenordnung
erwartungstreu bis auf Terme der Größenordnung
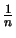 ist:
und dass der mittlere relative quadratische Schätzfehler von
ist:
und dass der mittlere relative quadratische Schätzfehler von
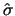 bis auf Terme kleinerer Größenordnung als
bis auf Terme kleinerer Größenordnung als
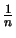 gegeben ist
durch
Mit dieser
Beziehung lässt sich die Zuverlässigkeit des Schätzers
gegeben ist
durch
Mit dieser
Beziehung lässt sich die Zuverlässigkeit des Schätzers
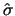 beurteilen.
beurteilen.
Wahl der Stichprobenparameter:
- a)
- Als Ausgangsdaten werden meist Tagesschlusskurse
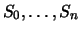 betrachtet.
betrachtet. 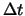 entspricht einem Tag bezogen
auf 1 Jahr, da
entspricht einem Tag bezogen
auf 1 Jahr, da  in der Regel die Jahresvolatilität ist.
Für Kalendertage wäre also
in der Regel die Jahresvolatilität ist.
Für Kalendertage wäre also
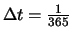 . Für
Wochenenden und Feiertage liegen allerdings keine Kurse vor. Die
folgende, empirisch begründete Argumentation legt aber nahe,
Wochenenden und Feiertage einfach zu ignorieren: Würde sich der
Kursprozess über das Wochenende genauso entwickeln wie unter der
Woche, auch wenn er nicht beobachtet wird, so müsste die
Standardabweichung der Kursänderung zwischen Freitag und Montag
das Dreifache der Standardabweichung der Kursänderung zwischen
zwei Werktagen, z.B. Montag und Dienstag, betragen. Dies folgt aus
der Beobachtung, dass für den Wiener-Prozess
. Für
Wochenenden und Feiertage liegen allerdings keine Kurse vor. Die
folgende, empirisch begründete Argumentation legt aber nahe,
Wochenenden und Feiertage einfach zu ignorieren: Würde sich der
Kursprozess über das Wochenende genauso entwickeln wie unter der
Woche, auch wenn er nicht beobachtet wird, so müsste die
Standardabweichung der Kursänderung zwischen Freitag und Montag
das Dreifache der Standardabweichung der Kursänderung zwischen
zwei Werktagen, z.B. Montag und Dienstag, betragen. Dies folgt aus
der Beobachtung, dass für den Wiener-Prozess
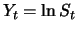 die
Standardabweichung der Änderung
die
Standardabweichung der Änderung
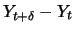 gerade
gerade
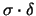 ist. Empirische Untersuchungen der
Aktienmärkte haben aber gezeigt, dass das Verhältnis der
Standardabweichungen nur wenig größer als 1 und auf jeden
Fall deutlich kleiner als 3 ist . Die Volatilität sinkt also
über das Wochenende, woraus man schließen kann, dass der
Handel selbst die Volatilität erhöht und sie nicht nur durch
externe Wirtschaftsentwicklungen bestimmt ist. Beim Schätzen der
Volatilität ist es daher ratsam, nur Handelstage zu betrachten,
an denen Kursnotierungen vorliegen. Üblicherweise rechnet man mit
252 Handelstagen pro Jahr, so dass
ist. Empirische Untersuchungen der
Aktienmärkte haben aber gezeigt, dass das Verhältnis der
Standardabweichungen nur wenig größer als 1 und auf jeden
Fall deutlich kleiner als 3 ist . Die Volatilität sinkt also
über das Wochenende, woraus man schließen kann, dass der
Handel selbst die Volatilität erhöht und sie nicht nur durch
externe Wirtschaftsentwicklungen bestimmt ist. Beim Schätzen der
Volatilität ist es daher ratsam, nur Handelstage zu betrachten,
an denen Kursnotierungen vorliegen. Üblicherweise rechnet man mit
252 Handelstagen pro Jahr, so dass
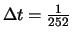 .
.
Bei monatlichen Daten ist entsprechend
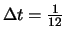 zu setzen. Wie schon in Abschnitt 3.3
ausgeführt erhalten wir etwa 19% Jahresvolatilität für die
monatlichen DAX Daten.
zu setzen. Wie schon in Abschnitt 3.3
ausgeführt erhalten wir etwa 19% Jahresvolatilität für die
monatlichen DAX Daten.
 SFMsumm.xpl
SFMsumm.xpl
- b)
-
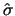 wird theoretisch immer zuverlässiger,
je
größer
wird theoretisch immer zuverlässiger,
je
größer  . In der Praxis ist die Volatilität aber über längere
Zeiträume nicht konstant, so dass lange zurückliegende Kurse wenig
aussagekräftig für das gegenwärtige
. In der Praxis ist die Volatilität aber über längere
Zeiträume nicht konstant, so dass lange zurückliegende Kurse wenig
aussagekräftig für das gegenwärtige  sind. Als Kompromiss
benutzt man oft die Schlusskurse der letzten 90 oder 180 Tage. Manche
Autoren empfehlen auch, um dieselbe Zeitspanne in die Vergangenheit
zurückzugehen, in der man die Volatilität in der Zukunft benutzen
will, also z.B. Kurse der Handelstage aus den letzten 9 Monaten zu
benutzen, wenn der Wert eines Calls mit Laufzeit 9 Monaten berechnet
werden soll.
sind. Als Kompromiss
benutzt man oft die Schlusskurse der letzten 90 oder 180 Tage. Manche
Autoren empfehlen auch, um dieselbe Zeitspanne in die Vergangenheit
zurückzugehen, in der man die Volatilität in der Zukunft benutzen
will, also z.B. Kurse der Handelstage aus den letzten 9 Monaten zu
benutzen, wenn der Wert eines Calls mit Laufzeit 9 Monaten berechnet
werden soll.
Die implizierte Volatilität (implied
volatility
- im deutschen Sprachgebrauch fälschlicherweise auch implizite Volatilität genannt ) einer Option wird nicht aus den
Aktienkursen, sondern aus den an der Terminbörse notierten
Optionen auf dieselbe Aktie berechnet. Betrachtet man einen
europäischen Call auf eine dividendenfreie Aktie
 , der an der Börse mit
, der an der Börse mit 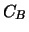 notiert wird, so ist seine
implizierte Volatilität
notiert wird, so ist seine
implizierte Volatilität 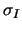 die Lösung der Gleichung
die Lösung der Gleichung
| |
|
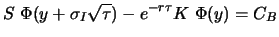 |
|
| |
|
|
|
| |
mit |
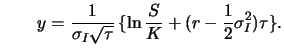 |
|
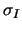 ist derjenige Wert der Volatilität
ist derjenige Wert der Volatilität  , für den der
nach der Black-Scholes-Formel (6.24) berechnete Optionswert
, für den der
nach der Black-Scholes-Formel (6.24) berechnete Optionswert 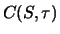 mit
dem beobachteten Marktwert übereinstimmt.
mit
dem beobachteten Marktwert übereinstimmt.  ist implizit als
Lösung der obigen Gleichung definiert und muss numerisch bestimmt
werden, da die Gleichung sich nicht nach
ist implizit als
Lösung der obigen Gleichung definiert und muss numerisch bestimmt
werden, da die Gleichung sich nicht nach  auflösen lässt.
auflösen lässt.
Die implizierte Volatilität kann benutzt werden, um sich einen
Eindruck über die Einschätzung des Marktes hinsichtlich
der Volatilität einer Aktie zu verschaffen. Man kann die
implizierten Volatilitäten aus (hinsichtlich Restlaufzeit  und Ausübungskurs
und Ausübungskurs  ) verschiedenen Optionen auf dieselbe Aktie
auch zu einem Schätzer von
) verschiedenen Optionen auf dieselbe Aktie
auch zu einem Schätzer von  kombinieren. Dabei sollte
man durch Gewichte die Stärke der Abhängigkeit des
Optionspreises von der Volatilität
berücksichtigen.
kombinieren. Dabei sollte
man durch Gewichte die Stärke der Abhängigkeit des
Optionspreises von der Volatilität
berücksichtigen.
 SFMVolSurfPlot.xpl
SFMVolSurfPlot.xpl
Beispiel 8.6
Zwei Optionen auf eine Aktie werden gehandelt. Eine von
ihnen ist am Geld und hat als implizierte Volatilität
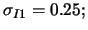
die andere ist weit im Geld und hat die implizierte Volatilität
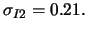
Am Geld ist die Abhängigkeit zwischen
Optionspreis und Volatilität besonders stark, so dass der Marktpreis
der ersten Option mehr Information über das

der Aktie enthält
und
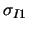
eine zuverlässigere Approximation von

ist. In der Kombination der beiden implizierten Volatilitäten zu einem
Schätzer
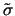
für

sollte
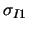
ein
größeres Gewicht erhalten, z.B.
Andere Autoren empfehlen,
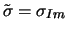
zu setzen,
wobei
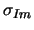
die implizierte Volatilität derjenigen Option auf
die Aktie ist, deren Wert am empfindlichsten auf Änderungen von

reagiert, d.h. der Option mit dem betragsgrößten Vega
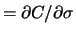
.
Soll die Methode risiko-neutraler Bewertung angewandt werden
(vgl. Cox and Ross (1976)),
muss das Maß derart transformiert werden, dass der resultierende Preisprozeß ein Martingal ist.
Dies garantiert die Abwesenheit von Arbitragemöglichkeiten (siehe Harrison and Kreps (1979)).
Bei unvollständigen Märkten gibt es jedoch eine Vielzahl solcher Transformationen (siehe Harrison and Pliska (1981)).
Im Gegensatz zu vollständigen Märkten kann der Händler bei
unvollständigen Märkten kein selbstfinanzierendes Portfolio
aufbauen, das die Auszahlung der Option exakt repliziert.
Daher ist das Hedgen nicht vollkommen risikolos, und Optionspreise hängen infolgedessen von den Risikopräferenzen ab. Es sollte an dieser Stelle
betont werden, dass das Fehlen einer perfekten Hedge-Strategie in der Praxis von eminenter Bedeutung ist.
![]() EUR, so kostet dies effektiv
EUR, so kostet dies effektiv
![]() EUR, also deutlich mehr als die durch den Verkauf
der Option erzielten Einnahmen. Steigt andererseits der Kurs nicht
über den Ausübungskurs
EUR, also deutlich mehr als die durch den Verkauf
der Option erzielten Einnahmen. Steigt andererseits der Kurs nicht
über den Ausübungskurs ![]() , so wird die Option nicht
ausgeübt, und die Bank kann 600000 EUR als Gewinn
verbuchen.
, so wird die Option nicht
ausgeübt, und die Bank kann 600000 EUR als Gewinn
verbuchen.
![]() SFMBSCopt2.xpl
SFMBSCopt2.xpl
![]() EUR. Wird im Falle
EUR. Wird im Falle ![]() die Option ausgeübt, so werden
die Aktien zum Preis von
die Option ausgeübt, so werden
die Aktien zum Preis von
![]() EUR
geliefert. Da dies abgezinst auf den Zeitpunkt
EUR
geliefert. Da dies abgezinst auf den Zeitpunkt ![]() ungefähr dem
ursprünglichen Kaufpreis der Aktien entspricht, beträgt der
Gewinn der Bank in diesem Fall rund 600000 EUR, d.h. dem
für den Verkauf der Option erzielten Betrag. Fällt dagegen der
Aktienkurs auf z.B.
ungefähr dem
ursprünglichen Kaufpreis der Aktien entspricht, beträgt der
Gewinn der Bank in diesem Fall rund 600000 EUR, d.h. dem
für den Verkauf der Option erzielten Betrag. Fällt dagegen der
Aktienkurs auf z.B. ![]() EUR, so wird die Option nicht
ausgeübt. Die Bank verliert aber aus dem Kursverlust der von ihr
gehaltenen Aktien rund 2000000 EUR, also wieder wesentlich
mehr als der für die Option erzielte Erlös. Aus der
Put-Call-Parität für europäische Optionen (Satz 2.3)
folgt übrigens, dass das Risiko aus dem Verkauf eines gedeckten
Calls identisch zum Risiko aus dem Verkauf eines ungedeckten Puts
ist.
EUR, so wird die Option nicht
ausgeübt. Die Bank verliert aber aus dem Kursverlust der von ihr
gehaltenen Aktien rund 2000000 EUR, also wieder wesentlich
mehr als der für die Option erzielte Erlös. Aus der
Put-Call-Parität für europäische Optionen (Satz 2.3)
folgt übrigens, dass das Risiko aus dem Verkauf eines gedeckten
Calls identisch zum Risiko aus dem Verkauf eines ungedeckten Puts
ist.
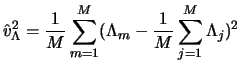
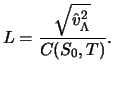
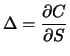 oder
oder 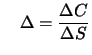
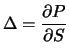
![\includegraphics[width=1.3\defpicwidth]{delta.ps}](sfmimg977.gif)
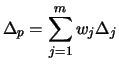
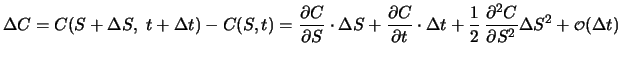
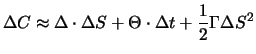
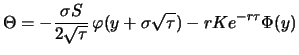
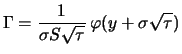
![\includegraphics[width=1.2\defpicwidth]{gamma.ps}](sfmimg1007.gif)
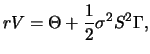
![\includegraphics[width=1.2\defpicwidth]{vega.ps}](sfmimg1029.gif)
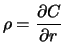
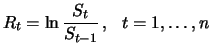
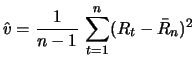
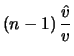
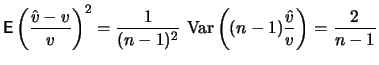
![$\displaystyle \mathop{\text{\rm\sf E}}[\hat{\sigma}] = \sigma + {\mathcal{O}}\left( \frac{1}{n}\right)\ , $](sfmimg1057.gif)