In diesem Abschnitt verwenden wir die Black-Scholes-Gleichung zur Berechnung des Preises europäischer Optionen.
Wir halten uns an die Notation des vorigen Kapitels und schreiben
für den Wert zur Zeit 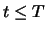 eines europäischen Calls bzw. Puts mit Ausübungskurs
eines europäischen Calls bzw. Puts mit Ausübungskurs  und
Fälligkeitstermin
und
Fälligkeitstermin  , wenn das zugrundeliegendes Objekt, z.B. eine Aktie, zur Zeit
, wenn das zugrundeliegendes Objekt, z.B. eine Aktie, zur Zeit  den Kurs
den Kurs 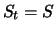 hat. Der
Wert der Kaufoption erfüllt dann für alle Kurse
hat. Der
Wert der Kaufoption erfüllt dann für alle Kurse 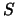 mit
mit
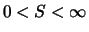 die Differentialgleichung
die Differentialgleichung
Die erste Randbedingung
(6.18) ergibt sich sofort aus der Definition des Calls, der
nur ausgeübt wird, wenn 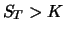 , und der dann den Gewinn
, und der dann den Gewinn
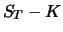 einbringt. Die erste Bedingung in (6.19) ergibt sich
aus der Beobachtung, dass die geometrische Brownsche Bewegung
einbringt. Die erste Bedingung in (6.19) ergibt sich
aus der Beobachtung, dass die geometrische Brownsche Bewegung
 in der Null bleibt, wenn sie erst einmal den Wert Null
angenommen hat, d.h. aus
in der Null bleibt, wenn sie erst einmal den Wert Null
angenommen hat, d.h. aus 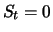 für ein
für ein 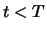 folgt
automatisch
folgt
automatisch 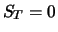 , und der Call wird nicht ausgeübt. Die
zweite Bedingung in (6.19) ergibt sich aus der Überlegung,
dass die geometrische Brownsche Bewegung
, und der Call wird nicht ausgeübt. Die
zweite Bedingung in (6.19) ergibt sich aus der Überlegung,
dass die geometrische Brownsche Bewegung  den Ausübungskurs
nur mit sehr geringer Wahrscheinlichkeit wieder unterschreitet,
wenn sie erst einmal ein Niveau weit oberhalb von
den Ausübungskurs
nur mit sehr geringer Wahrscheinlichkeit wieder unterschreitet,
wenn sie erst einmal ein Niveau weit oberhalb von  erreicht
hat. Wenn
erreicht
hat. Wenn 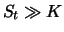 für ein
für ein 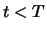 dann gilt auch mit hoher
Wahrscheinlichkeit
dann gilt auch mit hoher
Wahrscheinlichkeit 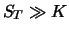 . Der Call wird also ausgeübt und
liefert den Ertrag
. Der Call wird also ausgeübt und
liefert den Ertrag
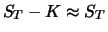 .
.
Die Differentialgleichung (6.17) mit den Randbedingungen (6.18), (6.19) kann analytisch gelöst werden.
Wir transformieren sie dazu in eine aus der Literatur bekannte Form. Zuerst ersetzen wir die Zeitvariable  durch
die Restlaufzeit
durch
die Restlaufzeit
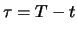 . Dadurch wird das Problem mit Endbedingung (6.18) bei
. Dadurch wird das Problem mit Endbedingung (6.18) bei 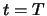 zu einem
Anfangswertproblem bei
zu einem
Anfangswertproblem bei 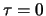 . Anschließend multiplizieren wir (6.17) mit
. Anschließend multiplizieren wir (6.17) mit
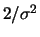 und ersetzen
die Parameter
und ersetzen
die Parameter 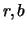 durch
durch
sowie die Variablen 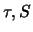 durch
Während für die alten Parameter
durch
Während für die alten Parameter
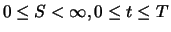 gegolten hat, ergibt sich für den
Wertebereich der neuen Parameter
Schließlich setzen wir
und erhalten die neue Differentialgleichung
gegolten hat, ergibt sich für den
Wertebereich der neuen Parameter
Schließlich setzen wir
und erhalten die neue Differentialgleichung
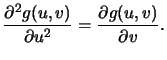 |
(8.20) |
mit der Anfangsbedingung
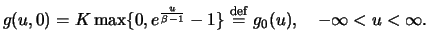 |
(8.21) |
Anfangswertprobleme dieser Art sind aus der Literatur über partielle Differentialgleichungen bestens bekannt. Sie
treten beispielsweise bei der mathematischen Modellierung von Wärmeleitungs- und Diffusionsprozessen auf. Die
Lösung ist
Den Optionspreis erhalten wir daraus, indem wir die Variablen- und Parametertransformationen
rückgängig machen. Wir schreiben im folgenden wieder wie in Kapitel 2.1 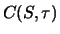 für den Call-Preis
als Funktion der Restlaufzeit
für den Call-Preis
als Funktion der Restlaufzeit
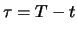 anstelle der aktuellen Zeit
anstelle der aktuellen Zeit  . Dann haben wir
Durch Substitution
. Dann haben wir
Durch Substitution
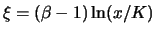 erhalten wir die Anfangsbedingung in ihrer ursprünglichen Form
erhalten wir die Anfangsbedingung in ihrer ursprünglichen Form
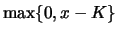 . Ersetzen wir außerdem
. Ersetzen wir außerdem 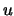 und
und 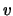 wieder durch die Variablen
wieder durch die Variablen 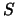 und
und 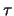 , erhalten wir
, erhalten wir
Für die geometrische Brownsche Bewegung ist 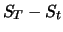 lognormalverteilt, d.h.
lognormalverteilt, d.h.
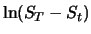 ist normalverteilt
mit den Parametern
ist normalverteilt
mit den Parametern
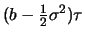 und
und
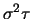 . Die bedingte Verteilung von
. Die bedingte Verteilung von 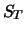 gegeben
gegeben
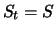 ist demnach ebenfalls eine Lognormalverteilung mit den Parametern
ist demnach ebenfalls eine Lognormalverteilung mit den Parametern
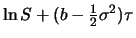 und
und
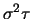 . Der Integrand von (6.22) ist aber bis auf den Faktor
. Der Integrand von (6.22) ist aber bis auf den Faktor
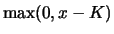 gerade die Dichte
dieser Verteilung. Damit erhalten wir die interessante Interpretation des Callwertes
gerade die Dichte
dieser Verteilung. Damit erhalten wir die interessante Interpretation des Callwertes 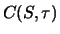 als abgezinster
Erwartungswert der Endbedingung
als abgezinster
Erwartungswert der Endbedingung
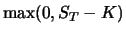 gegeben den aktuellen Kurs
gegeben den aktuellen Kurs 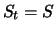 :
:
![$\displaystyle C(S,\tau) = e^{-r\tau} \mathop{\text{\rm\sf E}}[ \max ( 0,S_T-K) \, \vert \, S_t = S] .$](sfmimg901.gif) |
(8.23) |
Diese Eigenschaft ist bei der Herleitung numerischer Verfahren zur Berechnung von Optionswerten hilfreich. Zuerst
nutzen wir aber aus, dass (6.22) ein Integral bzgl. der Dichte einer Lognormalverteilung enthält, um den
Ausdruck weiter zu vereinfachen. Durch geeignete Substitution formen wir ihn in ein Integral bzgl. der Dichte
einer Normalverteilung um und erhalten
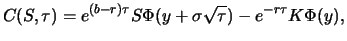 |
(8.24) |
wobei 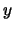 abkürzend für
abkürzend für
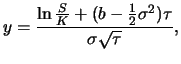 |
(8.25) |
steht und 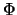 die Verteilungsfunktion der Standardnormalverteilung bezeichnet:
(6.24) ist zusammen mit (6.25) die Black-Scholes-Formel für den
Preis einer europäischen Kaufoption. In den Grenzfällen
die Verteilungsfunktion der Standardnormalverteilung bezeichnet:
(6.24) ist zusammen mit (6.25) die Black-Scholes-Formel für den
Preis einer europäischen Kaufoption. In den Grenzfällen 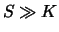 und
und 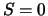 erhalten wir:
erhalten wir:
- Ist
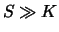 , so ist
, so ist 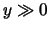 und damit
und damit
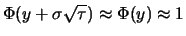 , so dass sich
der Wert der Kaufoption im dividendenfreien Fall
, so dass sich
der Wert der Kaufoption im dividendenfreien Fall 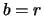 etwa wie
etwa wie
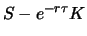 also wie der aktuelle Kurs abzüglich
des auf den aktuellen Zeitpunkt abgezinsten Ausübungskurses verhält.
also wie der aktuelle Kurs abzüglich
des auf den aktuellen Zeitpunkt abgezinsten Ausübungskurses verhält.
- Ist
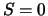 , so ist
, so ist
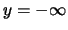 und somit
und somit
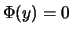 , so dass die Option wertlos ist:
, so dass die Option wertlos ist:
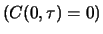 .
.
Die entsprechende Black-Scholes-Formel für den Preis 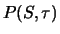 einer
europäischen Verkaufsoption könnten wir genauso durch Lösen der
Black-Scholes-Differentialgleichung mit den
passenden Randbedingungen herleiten. Einfacher ist aber das Ausnutzen der Put-Call-Parität (Satz 2.3)
Hieraus erhalten wir zusammen mit (6.24) sofort
einer
europäischen Verkaufsoption könnten wir genauso durch Lösen der
Black-Scholes-Differentialgleichung mit den
passenden Randbedingungen herleiten. Einfacher ist aber das Ausnutzen der Put-Call-Parität (Satz 2.3)
Hieraus erhalten wir zusammen mit (6.24) sofort
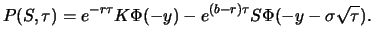 |
(8.26) |
Für den Wert europäischer Kauf- und Verkaufsoptionen gibt es
also explizite Formeln. Die beiden Terme in der Formel (6.24)
für z.B. den Wert der Kaufoption lassen sich grob
folgendermaßen interpretieren, wobei wir uns auf den
dividendenfreien Fall 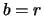 beschränken. Der erste Term ist dann
beschränken. Der erste Term ist dann
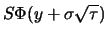 und repräsentiert in erster Linie
den Wert der Aktie, die der Käufer der Kaufoption im Fall der
Ausübung seines Rechts beziehen kann. Der andere Term
und repräsentiert in erster Linie
den Wert der Aktie, die der Käufer der Kaufoption im Fall der
Ausübung seines Rechts beziehen kann. Der andere Term
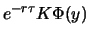 steht in erster Linie für den Wert des
Ausübungskurses. Über die Variable
steht in erster Linie für den Wert des
Ausübungskurses. Über die Variable 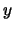 beeinflusst natürlich
das Verhältnis
beeinflusst natürlich
das Verhältnis 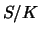 beide Terme.
beide Terme.
Bei der Herleitung der Black-Scholes-Differentialgleichung haben wir gesehen, dass insbesondere der Wert einer
Kaufoption durch Aktien und Anleihen dupliziert werden kann. Der in Aktien
investierte Betrag ergibt sich dabei als
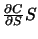 ,
wobei
,
wobei
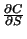 die Hedge-Rate ist. Sie
bestimmt das zum Hedgen notwendige, auch Delta genannte Verhältnis zwischen Aktien und Optionen.
Leitet man die Black-Scholes-Formel (6.24) nach
die Hedge-Rate ist. Sie
bestimmt das zum Hedgen notwendige, auch Delta genannte Verhältnis zwischen Aktien und Optionen.
Leitet man die Black-Scholes-Formel (6.24) nach 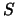 ab, so erhält man
ab, so erhält man
Der erste Term in (6.24) steht somit für den im
Duplikationsportfolio in Aktien und der zweite für den in
Anleihen investierten Betrag.
Da die analytischen Lösungsformeln die Auswertung der Standardnormalverteilungsfunktion erfordert,
was nur numerisch erfolgen kann, muss man für die praktische Anwendung der Black-Scholes-Formel auf
Näherungen der Normalverteilung zurückgreifen. Davon kann in geringem Maße der berechnete Optionswert
abhängen. Zur Illustration betrachten wir verschiedene in der Literatur (beispielsweise Hastings (1955))
beschriebene Näherungsformeln.
a.) Die Normalverteilung kann folgendermaßen approximiert werden:
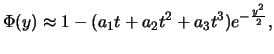
mit
Der Approximationsfehler hat unabhängig von 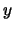 die Größenordnung
die Größenordnung
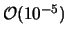 .
.
 SFMNormalApprox1.xpl
SFMNormalApprox1.xpl
b.)
Der Fehler dieser Approximation liegt bei
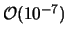 .
.
 SFMNormalApprox2.xpl
SFMNormalApprox2.xpl
c.) Eine andere Approximation der Normalverteilung, deren
Fehler von der Größenordnung
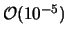 ist, lautet:
ist, lautet:
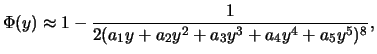
mit
 SFMNormalApprox3.xpl
SFMNormalApprox3.xpl
d.) Als letzte Möglichkeit wollen wir hier noch
die Taylorreihenzerlegung angeben:
Mit Hilfe dieser Reihe kann die Normalverteilung beliebig genau angenähert
werden, wobei natürlich mit der Genauigkeit auch die Anzahl der benötigten
Summanden und somit der arithmetischen Operationen steigt.
 SFMNormalApprox4.xpl
SFMNormalApprox4.xpl
Ein Vergleich aller vier Näherungsformeln ist in der Tabelle 6.1 enthalten.
Die Taylorreihe wurde beim ersten Summanden, der betragsmäßig kleiner
als 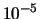 ist, abgebrochen. Die letzte Spalte gibt dabei die Nummer
des letzten Summanden an.
ist, abgebrochen. Die letzte Spalte gibt dabei die Nummer
des letzten Summanden an.
Tabelle 6.1:
Verschiedene Approximationen der Normalverteilung
 |
norm-a |
norm-b |
norm-c |
norm-d |
iter |
|
1.0000 |
0.8413517179 |
0.8413447362 |
0.8413516627 |
0.8413441191 |
6 |
|
1.1000 |
0.8643435425 |
0.8643338948 |
0.8643375717 |
0.8643341004 |
7 |
|
1.2000 |
0.8849409364 |
0.8849302650 |
0.8849298369 |
0.8849309179 |
7 |
|
1.3000 |
0.9032095757 |
0.9031994476 |
0.9031951398 |
0.9031993341 |
8 |
|
1.4000 |
0.9192515822 |
0.9192432862 |
0.9192361959 |
0.9192427095 |
8 |
|
1.5000 |
0.9331983332 |
0.9331927690 |
0.9331845052 |
0.9331930259 |
9 |
|
1.6000 |
0.9452030611 |
0.9452007087 |
0.9451929907 |
0.9452014728 |
9 |
|
1.7000 |
0.9554336171 |
0.9554345667 |
0.9554288709 |
0.9554342221 |
10 |
|
1.8000 |
0.9640657107 |
0.9640697332 |
0.9640670474 |
0.9640686479 |
10 |
|
1.9000 |
0.9712768696 |
0.9712835061 |
0.9712842148 |
0.9712839202 |
11 |
|
2.0000 |
0.9772412821 |
0.9772499371 |
0.9772538334 |
0.9772496294 |
12 |
|
Tabelle:
Bestimmung des europäischen Callpreises mit verschiedenen Approximationen der Normalverteilung
 SFMBSCopt1.xpl
SFMBSCopt1.xpl
Aktienkurs  |
230.00 |
EUR/Aktie |
Ausübungskurs  |
210.00 |
EUR/Aktie |
stetiger Zinssatz 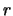 |
0.04545 |
|
stetiger Bestandshaltekosten 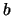 |
0.04545 |
keine Dividende |
Volatilität  |
0.25000 |
p.a. |
Restlaufzeit
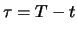 |
0.50000 |
a |
| Optionspreise norm-a |
30.74262 |
|
| Optionspreise norm-b |
30.74158 |
|
| Optionspreise norm-c |
30.74352 |
|
| Optionspreise norm-d |
30.74157 |
|
|
Die Tabelle 6.2 zeigt den Optionspreis, der mit Hilfe der
Formel (6.24) für eine konkrete europäische Kaufoption
auf der Grundlage verschiedener Approximationen der
Normalverteilung berechnet wurde.
![]() durch
die Restlaufzeit
durch
die Restlaufzeit
![]() . Dadurch wird das Problem mit Endbedingung (6.18) bei
. Dadurch wird das Problem mit Endbedingung (6.18) bei ![]() zu einem
Anfangswertproblem bei
zu einem
Anfangswertproblem bei ![]() . Anschließend multiplizieren wir (6.17) mit
. Anschließend multiplizieren wir (6.17) mit
![]() und ersetzen
die Parameter
und ersetzen
die Parameter ![]() durch
durch
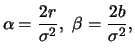

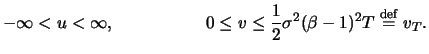
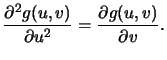
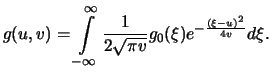
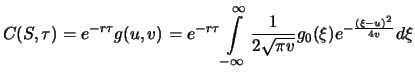
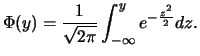
![]() ,
wobei
,
wobei
![]() die Hedge-Rate ist. Sie
bestimmt das zum Hedgen notwendige, auch Delta genannte Verhältnis zwischen Aktien und Optionen.
Leitet man die Black-Scholes-Formel (6.24) nach
die Hedge-Rate ist. Sie
bestimmt das zum Hedgen notwendige, auch Delta genannte Verhältnis zwischen Aktien und Optionen.
Leitet man die Black-Scholes-Formel (6.24) nach ![]() ab, so erhält man
ab, so erhält man
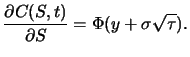
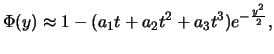 mit
mit
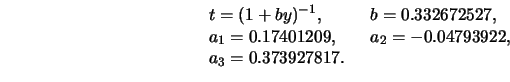
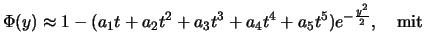
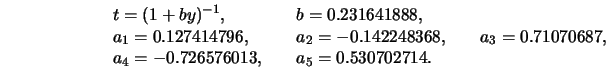
![]() ist, lautet:
ist, lautet:
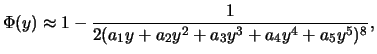 mit
mit
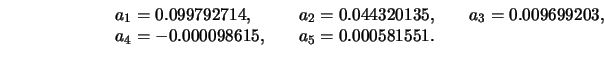
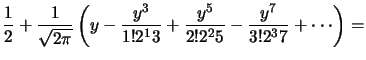
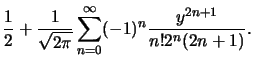
![]() ist, abgebrochen. Die letzte Spalte gibt dabei die Nummer
des letzten Summanden an.
ist, abgebrochen. Die letzte Spalte gibt dabei die Nummer
des letzten Summanden an.