Einfache, allgemein akzeptierte ökonomische Annahmen reichen
nicht aus, um eine rationale Optionspreistheorie zu entwickeln.
Die Voraussetzung eines perfekten Marktes hat in Kapitel
2.1 nur zum Herleiten elementarer Arbitragebeziehungen
gereicht, denen Optionspreise genügen müssen und die sich
daher als Test für fortgeschrittene Modellierungsansätze
eignen. Die explizite Berechnung eines Optionspreises als Funktion
von Zeit und Kurs sowie seiner zugrundeliegenden Parameter 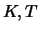 ist damit aber nicht möglich. Hierfür wird ein Modell für
den Kurs des zugrundeliegenden Finanzinstruments (Aktie, Devise,
...) gebraucht, bei dem es sich in aller Regel um einen
stochastischen Prozess in diskreter oder stetiger Zeit handelt.
Prozesse in stetiger Zeit haben den Vorteil, dass sich mit ihnen
viele Problemstellungen leichter analytisch behandeln lassen.
Prozesse in diskreter Zeit betrachten wir vorerst nur als
Approximationen, mit denen sich leichter numerische Berechnungen
durchführen lassen. Im zweiten Teil des Buches werden sie als
eigenständige Modelle in der Finanzzeitreihenanalyse diskutiert.
ist damit aber nicht möglich. Hierfür wird ein Modell für
den Kurs des zugrundeliegenden Finanzinstruments (Aktie, Devise,
...) gebraucht, bei dem es sich in aller Regel um einen
stochastischen Prozess in diskreter oder stetiger Zeit handelt.
Prozesse in stetiger Zeit haben den Vorteil, dass sich mit ihnen
viele Problemstellungen leichter analytisch behandeln lassen.
Prozesse in diskreter Zeit betrachten wir vorerst nur als
Approximationen, mit denen sich leichter numerische Berechnungen
durchführen lassen. Im zweiten Teil des Buches werden sie als
eigenständige Modelle in der Finanzzeitreihenanalyse diskutiert.
Ein auch heute noch häufig verwendetes Modell für Aktienkurse, das auch die Grundlage des klassischen
Black-Scholes-Ansatzes darstellt, ist die geometrische Brownsche Bewegung. Bei Annahme dieses Modells erfüllt der Aktienkurs  die einfache
stochastische Differentialgleichung
die einfache
stochastische Differentialgleichung
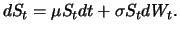 |
(8.1) |
Äquivalent hierzu ist die Annahme, dass der Prozess der Renditen eine gewöhnliche Brownsche Bewegung
ist, d.h.
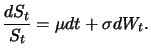 |
(8.2) |
Die Drift 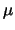 gibt die erwartete Rendite des Objektes je
Zeiteinheit. Die Volatilität
gibt die erwartete Rendite des Objektes je
Zeiteinheit. Die Volatilität  ist ein Maß für die
zu erwartende Größe der zufälligen Schwankungen der
Rendite um ihren Erwartungswert.
ist ein Maß für die
zu erwartende Größe der zufälligen Schwankungen der
Rendite um ihren Erwartungswert. 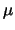 und
und  hängen
voneinander ab und sind für Anlageentscheidungen auf der Basis
von Risikopräferenzen wesentlich: je größer die erwartete
Rendite, also
hängen
voneinander ab und sind für Anlageentscheidungen auf der Basis
von Risikopräferenzen wesentlich: je größer die erwartete
Rendite, also 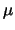 , sein soll, ein umso höheres, durch
, sein soll, ein umso höheres, durch  quantifiziertes Risiko muss in der Regel eingegangen werden.
quantifiziertes Risiko muss in der Regel eingegangen werden.
Das Modell der geometrischen Brownschen Bewegung liefert eine
brauchbare und in der Praxis bewährte Näherung für
Aktienkurse über kurze und mittlere Zeiträume, zum Beispiel
über die Laufzeit typischer Aktienoptionen. Inzwischen sind zwar
eine Reihe von Diskrepanzen zwischen Realität und Modell
bekannt, z.B. Abweichungen der Volatilitätsfunktion
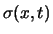 im allgemeinen Modell (5.8) von der linearen
Form
im allgemeinen Modell (5.8) von der linearen
Form
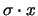 der geometrischen Brownschen Bewegung in
bestimmten Situationen, aber der Black-Scholes-Ansatz wird dennoch
als erste einfache Näherung zur Optionsbewertung benutzt. Die
prinzipielle Idee zur Ableitung von Optionspreisen lässt sich
außerdem auf allgemeinere Aktienkursmodelle übertragen.
der geometrischen Brownschen Bewegung in
bestimmten Situationen, aber der Black-Scholes-Ansatz wird dennoch
als erste einfache Näherung zur Optionsbewertung benutzt. Die
prinzipielle Idee zur Ableitung von Optionspreisen lässt sich
außerdem auf allgemeinere Aktienkursmodelle übertragen.
Der Ansatz von Black und Scholes beruht auf der bereits in Kapitel
2.1 benutzten Idee, den Wert eines Portfolios, das die
interessierende Option enthält, durch ein zweites Portfolio zu
duplizieren, das ausschließlich aus Finanzinstrumenten mit
bekanntem Preis besteht. Dieses Duplikationsportfolio
wird so gewählt, dass beide
Portfolios zu einem Zeitpunkt  , typischerweise dem
Fälligkeitstermin der Option, wertgleich sind. Dann folgt aus
der Annahme eines perfekten Marktes und insbesondere aus der
Arbitragefreiheit die Wertgleichheit zu jedem früheren
Zeitpunkt. Hierfür gibt es zwei äquivalente Möglichkeiten,
die wir am Beispiel eines Calls auf eine Aktie mit Kurs
, typischerweise dem
Fälligkeitstermin der Option, wertgleich sind. Dann folgt aus
der Annahme eines perfekten Marktes und insbesondere aus der
Arbitragefreiheit die Wertgleichheit zu jedem früheren
Zeitpunkt. Hierfür gibt es zwei äquivalente Möglichkeiten,
die wir am Beispiel eines Calls auf eine Aktie mit Kurs  erläutern:
erläutern:
1. Eines der Portfolios besteht nur aus dem Call, dessen Preis ermittelt werden soll. Das Duplikationsportfolio
wird aus Aktien und risikolosen Zerobonds zusammengestellt, deren Anzahl sich kontinuierlich an den sich
ändernden Kurs anpassen müssen. Der Nominalwert der Zerobonds kann ohne Einschränkung als 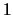 gesetzt
werden, da ihre Anzahl frei wählbar ist. Zur Zeit
gesetzt
werden, da ihre Anzahl frei wählbar ist. Zur Zeit  bestehen die beiden Portfolios aus
bestehen die beiden Portfolios aus
- Portfolio
 :
:
- Eine Kaufoption auf die Aktie mit Terminkurs
 und Fälligkeit
und Fälligkeit  .
.
- Portfolio
 :
:
-
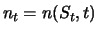 Aktien und
Aktien und
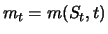 Zerobonds mit Nominalwert
Zerobonds mit Nominalwert 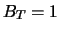 und
Fälligkeit
und
Fälligkeit  .
.
2. Eines der Portfolios ist ein perfektes Hedge-Portefeuille aus Aktien und
verkauften Calls (mit Short Selling). Durch eine dynamische Hedge-Strategie wird dafür gesorgt, dass das
Portfolio jederzeit risikolos ist, d.h. dass die Calls gerade die Gewinne und Verluste der Aktien neutralisieren.
Das Duplikationsportfolio ist dementsprechend ebenfalls risikofrei und besteht ausschließlich aus Zerobonds.
Auch dieser Ansatz erfordert wie im Fall 1. eine kursabhängige kontinuierliche Anpassung im Bestand der Portfolios.
Zur Zeit  enthalten die beiden Portfolios
enthalten die beiden Portfolios
- Portfolio
 :
:
- Eine Aktie und
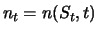 (über Short selling) verkaufte Kaufoptionen auf die
Aktie mit Terminkurs
(über Short selling) verkaufte Kaufoptionen auf die
Aktie mit Terminkurs  und Fälligkeit
und Fälligkeit  .
.
- Portfolio
 :
:
-
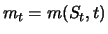 Zerobonds mit Nominalwert
Zerobonds mit Nominalwert 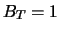 und Fälligkeit
und Fälligkeit  .
.
Sei 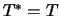 , wenn der Besitzer die Kaufoption verfallen lässt,
und sei
, wenn der Besitzer die Kaufoption verfallen lässt,
und sei 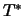 andernfalls der Zeitpunkt, zu dem die Option
ausgeübt wird. Für einen europäischen Call ist z.B. stets
andernfalls der Zeitpunkt, zu dem die Option
ausgeübt wird. Für einen europäischen Call ist z.B. stets
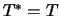 , während ein amerikanischer Call vorzeitig ausgeübt
werden kann. Aus der Wertgleichheit des Calls und des
Duplikationsportfolios in Ansatz 1. oder aus der Wertgleichheit
des Hedgeportfolios mit dem risikolosen Bondportfolio in Ansatz 2.
zu jedem Zeitpunkt
, während ein amerikanischer Call vorzeitig ausgeübt
werden kann. Aus der Wertgleichheit des Calls und des
Duplikationsportfolios in Ansatz 1. oder aus der Wertgleichheit
des Hedgeportfolios mit dem risikolosen Bondportfolio in Ansatz 2.
zu jedem Zeitpunkt
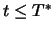 folgt jeweils dieselbe partielle
Differentialgleichung für den Wert des Calls, die sogenannte
Black-Scholes-Gleichung.
folgt jeweils dieselbe partielle
Differentialgleichung für den Wert des Calls, die sogenannte
Black-Scholes-Gleichung.
Der Ansatz von Black und Scholes ist nicht auf die Preisbestimmung
einfacher Puts und Calls beschränkt, sondern lässt sich auf
jedes derivative Finanzinstrument 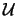 auf ein
zugrundeliegendes Objekt mit Kurs
auf ein
zugrundeliegendes Objekt mit Kurs  anwenden, wenn
anwenden, wenn  eine
geometrische Brownsche Bewegung ist und wenn der Preis
eine
geometrische Brownsche Bewegung ist und wenn der Preis 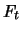 des
Derivats bis zu seiner Ausübung nur eine Funktion des aktuellen
Kurses und der Zeit ist:
des
Derivats bis zu seiner Ausübung nur eine Funktion des aktuellen
Kurses und der Zeit ist:
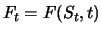 . Dann existiert nach dem
folgenden Satz ein das Finanzinstrument duplizierendes Portfolio
und der obige Ansatz 1. ist auf die Preisbestimmung anwendbar. Bei
allgemeinen Derivaten muss das Duplikationsportfolio nicht nur zum
Ausübungszeitpunkt
. Dann existiert nach dem
folgenden Satz ein das Finanzinstrument duplizierendes Portfolio
und der obige Ansatz 1. ist auf die Preisbestimmung anwendbar. Bei
allgemeinen Derivaten muss das Duplikationsportfolio nicht nur zum
Ausübungszeitpunkt 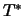 denselben Wert haben, sondern auch
vorher schon denselben Cashflow, d.h. dieselben
entnehmbaren Erträge oder zuzuschießenden Kosten, wie das
Derivat generieren. Die Existenz eines perfekten Hedge-Portfolios
als Grundlage von Ansatz 2. kann analog gezeigt werden.
denselben Wert haben, sondern auch
vorher schon denselben Cashflow, d.h. dieselben
entnehmbaren Erträge oder zuzuschießenden Kosten, wie das
Derivat generieren. Die Existenz eines perfekten Hedge-Portfolios
als Grundlage von Ansatz 2. kann analog gezeigt werden.
Satz 8.1
Sei der Kurs

eines Objektes eine geometrische Brownsche
Bewegung (
6.1). Sei
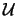
ein von dem Objekt
abhängiges derivatives Finanzinstrument mit Fälligkeit

.
Sei
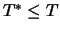
der Ausübungszeitpunkt des Derivats bzw.
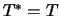
, falls
nicht ausgeübt wird. Sei der Wert des
Derivats zu jedem Zeitpunkt
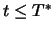
durch eine Funktion
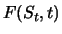
von Kurs und Zeit gegeben.
- a)
- Es existiert ein Portfolio aus dem zugrundeliegenden
Objekt und risikolosen Anleihen, das das Derivat in dem Sinn
dupliziert, dass es bis zur Zeit
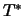 denselben Cashflow
generiert und zur Zeit
denselben Cashflow
generiert und zur Zeit 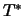 denselben Wert wie
denselben Wert wie 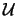 hat.
hat.
- b)
- Die Wertfunktion
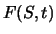 des Derivats erfüllt die
Differentialgleichung von Black und Scholes
des Derivats erfüllt die
Differentialgleichung von Black und Scholes
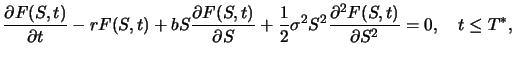 |
(8.3) |
Beweis:
Der Einfachheit halber gehen wir davon aus, dass das Objekt eine
Aktie mit dem stetigen Dividendenertrag 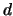 und damit den
Bestandshaltekosten
und damit den
Bestandshaltekosten 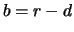 ist, wobei
ist, wobei 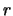 wieder den
kontinuierlichen Zinssatz bezeichnet. Wir beschränken uns
außerdem auf den Fall, dass
wieder den
kontinuierlichen Zinssatz bezeichnet. Wir beschränken uns
außerdem auf den Fall, dass 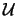 ein Derivat mit der
Aktie als zugrundeliegendem Objekt ist und dass
ein Derivat mit der
Aktie als zugrundeliegendem Objekt ist und dass 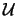 vor der
Zeit
vor der
Zeit 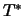 keinen Cashflow erzeugt.
keinen Cashflow erzeugt.
Wir bilden ein Portfolio aus
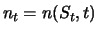 Aktien und aus
Aktien und aus
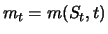 Zerobonds mit Fälligkeit
Zerobonds mit Fälligkeit  und
Nominalwert
und
Nominalwert 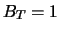 .
.
sei der auf den Zeitpunkt  abgezinste Wert eines Bonds. Den Wert des Portfolios zur Zeit
abgezinste Wert eines Bonds. Den Wert des Portfolios zur Zeit  bezeichnen
wir mit
Zu zeigen ist, dass
bezeichnen
wir mit
Zu zeigen ist, dass 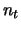 und
und 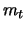 so gewählt werden können,
dass bei Ausübung bzw. am Ende der Laufzeit von
so gewählt werden können,
dass bei Ausübung bzw. am Ende der Laufzeit von 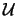 Portfolio und Derivat wertgleich sind, d.h.
Portfolio und Derivat wertgleich sind, d.h.
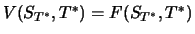 , und dass das Portfolio vorher keinen Cashflow
erzeugt, d.h. dem Portfolio darf vor der Zeit
, und dass das Portfolio vorher keinen Cashflow
erzeugt, d.h. dem Portfolio darf vor der Zeit 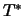 weder Geld
entnommen noch ihm Geld zugeschossen werden. Alle Änderungen im
Bestand müssen aus den Dividenden bzw. durch Kauf und Verkauf
von Aktien bzw. Bonds realisiert werden.
weder Geld
entnommen noch ihm Geld zugeschossen werden. Alle Änderungen im
Bestand müssen aus den Dividenden bzw. durch Kauf und Verkauf
von Aktien bzw. Bonds realisiert werden.
Wir untersuchen zuerst, wie sich der Wert 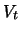 des Portfolios in einem kleinen Zeitraum
des Portfolios in einem kleinen Zeitraum 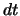 ändert. Dabei
schreiben wir
ändert. Dabei
schreiben wir
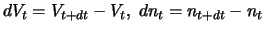 usw.
usw.
so dass
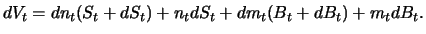 |
(8.4) |
Da der stochastische Prozess  eine geometrische Brownsche Bewegung und damit ein
Itô-Prozess (5.8) mit
eine geometrische Brownsche Bewegung und damit ein
Itô-Prozess (5.8) mit
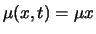 und
und
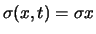 ist, folgt aus der allgemeinen
Form (5.10) des Lemmas von Itô zusammen mit (6.1)
ist, folgt aus der allgemeinen
Form (5.10) des Lemmas von Itô zusammen mit (6.1)
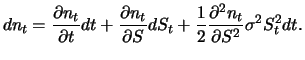 |
(8.5) |
und eine völlig analoge Beziehung für 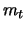 . Daraus folgt unter Verwendung von
. Daraus folgt unter Verwendung von
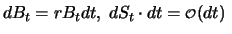
und
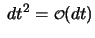
und Vernachlässigen der Terme, die klein gegenüber 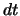 sind:
sind:
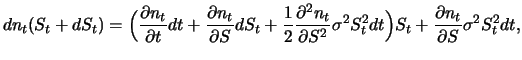 |
(8.6) |
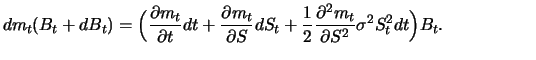 |
(8.7) |
Die entscheidende Forderung, dass das Portfolio wie das zu duplizierende Derivat vor der Zeit 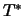 keinen Cashflow
generiert, bedeutet nun, dass die beiden Komponenten
keinen Cashflow
generiert, bedeutet nun, dass die beiden Komponenten
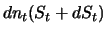 und
und
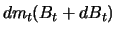 von
von
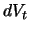 in (6.4), die dem Kauf/Verkauf von Aktien bzw. Zerobonds
entsprechen, aus den Dividenden finanziert werden müssen. Da eine Aktie in einem kleinen Zeitintervall der
Länge
in (6.4), die dem Kauf/Verkauf von Aktien bzw. Zerobonds
entsprechen, aus den Dividenden finanziert werden müssen. Da eine Aktie in einem kleinen Zeitintervall der
Länge 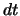 die Dividende
die Dividende
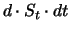 abwirft, bedeutet dies
oder, nach Einsetzen von (6.6) und (6.7),
abwirft, bedeutet dies
oder, nach Einsetzen von (6.6) und (6.7),
Einsetzen von (6.1) und Zusammenfassen der stochastischen Anteile mit Differential 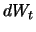 , der
deterministischen Anteile mit Differential
, der
deterministischen Anteile mit Differential 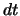 , die den Driftparameter
, die den Driftparameter 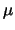 enthalten, und der
restlichen deterministischen Terme liefert
enthalten, und der
restlichen deterministischen Terme liefert
Dies ist nur möglich, wenn der stochastische Anteil verschwindet, d.h.
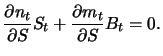 |
(8.9) |
Damit verschwindet der erste Term in (6.8) ebenfalls, und der mittlere Term muss schließlich auch 0 sein:
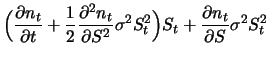 |
|
|
|
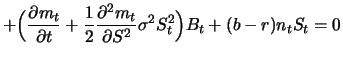 |
|
|
(8.10) |
Wir können diese Gleichung weiter vereinfachen, indem wir Gleichung (6.9) partiell nach 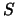 differenzieren:
differenzieren:
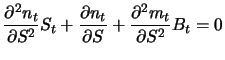 |
(8.11) |
und das Ergebnis in (6.10) einsetzen. Wir erhalten dann
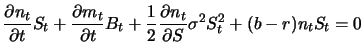 |
(8.12) |
Da der Aktienkurs  nicht explizit von der Zeit abhängt und somit
nicht explizit von der Zeit abhängt und somit
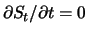 , liefert
Differenzieren des Portfoliowerts
, liefert
Differenzieren des Portfoliowerts
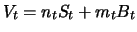 nach der Zeit
Daraus folgt
Durch Einsetzen dieser Gleichung in (6.12) eliminieren wir den
nach der Zeit
Daraus folgt
Durch Einsetzen dieser Gleichung in (6.12) eliminieren wir den 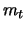 enthaltenden Term und erhalten
enthaltenden Term und erhalten
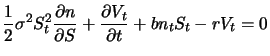 |
(8.13) |
Da der Bondwert 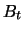 nicht vom Kurs abhängt und somit
nicht vom Kurs abhängt und somit
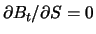 , liefert
Differenzieren des Portfoliowerts
, liefert
Differenzieren des Portfoliowerts
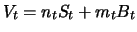 nach dem Kurs
wegen Gleichung (6.9), d.h.
nach dem Kurs
wegen Gleichung (6.9), d.h.
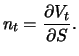 |
(8.14) |
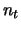 ist somit gleich dem sogenannten Delta oder der Hedge-Rate des Portfolios (vgl. Abschnitt 6.3.1). Da
können wir das gesuchte Duplikationsportfolio konstruieren, wenn
wir
ist somit gleich dem sogenannten Delta oder der Hedge-Rate des Portfolios (vgl. Abschnitt 6.3.1). Da
können wir das gesuchte Duplikationsportfolio konstruieren, wenn
wir
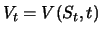 kennen. Diese Funktion von Kurs und
Zeit erhalten wir als Lösung der Differentialgleichung
von Black und Scholes
kennen. Diese Funktion von Kurs und
Zeit erhalten wir als Lösung der Differentialgleichung
von Black und Scholes
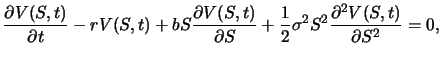 |
(8.15) |
die sich durch Einsetzen von (6.14) in Gleichung (6.13) ergibt. Zur Bestimmung von 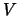 fehlt noch ein
Randbedingung, die wir aus der Forderung erhalten, dass der Cashflow des Portfolios bei Ausübung bzw. Fälligkeit des
Derivats, d.h. zur Zeit
fehlt noch ein
Randbedingung, die wir aus der Forderung erhalten, dass der Cashflow des Portfolios bei Ausübung bzw. Fälligkeit des
Derivats, d.h. zur Zeit 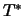 , mit dem Cashflow des Derivats übereinstimmt, also denselben Pay-off hat:
, mit dem Cashflow des Derivats übereinstimmt, also denselben Pay-off hat:
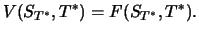 |
(8.16) |
Da das Derivat jederzeit denselben Cashflow wie das Portfolio hat, erfüllt 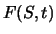 ebenfalls die Black-Scholes-
Differentialgleichung, und zu jedem Zeitpunkt
ebenfalls die Black-Scholes-
Differentialgleichung, und zu jedem Zeitpunkt
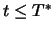 gilt
gilt
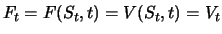 .
.

Die Differentialgleichung von Black und Scholes beruht wesentlich
auf der Annahme, dass der Kurs durch eine geometrische Brownsche
Bewegung modelliert werden kann. Eine derartige Annahme ist nur
gerechtfertigt, wenn die darauf aufbauende Theorie auch die
Arbitragebeziehungen aus Kapitel 2.1 reproduziert, Wir
überprüfen dies am Beispiel eines Terminkontraktes mit
Terminkurs  und Fälligkeit
und Fälligkeit  auf ein Objekt, mit dem
stetige Bestandshaltekosten mit Rate
auf ein Objekt, mit dem
stetige Bestandshaltekosten mit Rate 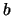 verbunden sind. Der Wert
verbunden sind. Der Wert
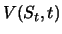 hängt nur von Kurs und Zeit ab, erfüllt also die
Bedingung von Satz 6.1. Aus Satz 2.1 erhalten wir
nach Einsetzen der Definition der Restlaufzeit
hängt nur von Kurs und Zeit ab, erfüllt also die
Bedingung von Satz 6.1. Aus Satz 2.1 erhalten wir
nach Einsetzen der Definition der Restlaufzeit
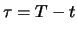 Durch Einsetzen überprüft man leicht, dass diese Funktion die
eindeutige Lösung der Differentialgleichung (6.3) mit
der Randbedingung
Durch Einsetzen überprüft man leicht, dass diese Funktion die
eindeutige Lösung der Differentialgleichung (6.3) mit
der Randbedingung
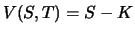 ist. Der Black-Scholes-Ansatz
liefert also denselben Preis des Terminkontrakts wie die
modellfreie Arbitragebeziehung.
ist. Der Black-Scholes-Ansatz
liefert also denselben Preis des Terminkontrakts wie die
modellfreie Arbitragebeziehung.
Zum Schluss bemerken wir noch, dass das Modell der geometrischen Brownschen Bewegung für Aktienkurse
über mittelgroße Zeiträume eine brauchbare Näherung liefert. Die Übertragung des Modells auf andere
grundlegende Finanzinstrumente wie Devisen oder Anleihen ist nicht ohne weiteres möglich. Bondoptionen
haben in der Regel eine deutlich längere Laufzeit als Aktienoptionen. Ihre Wertentwicklung
hängt nicht vom Kurs, sondern von dem dann ebenfalls als stochastischer Prozess aufzufassenden Zins ab.
Zur adäquaten Modellierung der Zinsentwicklung braucht man aber andere Arten stochastischer Prozesse, die
wir in späteren Kapiteln diskutieren werden.
Wechselkurse lassen sich eingeschränkt als geometrische
Brownsche Bewegung modellieren. Empirische Vergleiche zeigen, dass
dieses Modell für manche Währungen oder Laufzeiten nicht
geeignet ist, so dass im Einzelfall anhand von Daten überprüft
werden muss, ob der Black-Scholes-Ansatz für die Bewertung von
Devisenoptionen benutzt werden kann. Ist dies der Fall, so
entspricht die Fremdwährung, die das zugrundeliegende Objekt der
Option ist, einer Aktie mit einem kontinuierlichen
Dividendenertrag, der durch die kontinuierliche Zinsrate 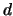 im
Land der Fremdwährung gegeben ist. Die Bestandshaltekosten
im
Land der Fremdwährung gegeben ist. Die Bestandshaltekosten 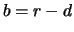 entsprechen der Differenz der Zinsen im Inland und im Land
der Fremdwährung: Kauft der Investor die Fremdwährung
vorzeitig, so kann er sein Kapital nicht mehr im Inland anlegen
und verliert den Zinssatz
entsprechen der Differenz der Zinsen im Inland und im Land
der Fremdwährung: Kauft der Investor die Fremdwährung
vorzeitig, so kann er sein Kapital nicht mehr im Inland anlegen
und verliert den Zinssatz 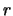 , gewinnt dafür aber den Zinssatz
, gewinnt dafür aber den Zinssatz
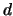 , den er für die Fremdwährung in deren Herkunftsland
erhält. Der Wert der Devisenoption ergibt
sich dann durch Lösen der Differentialgleichung (6.3)
von Black und Scholes mit der passenden, durch den Typ der Option
bestimmten Randbedingung.
, den er für die Fremdwährung in deren Herkunftsland
erhält. Der Wert der Devisenoption ergibt
sich dann durch Lösen der Differentialgleichung (6.3)
von Black und Scholes mit der passenden, durch den Typ der Option
bestimmten Randbedingung.
![]() ist damit aber nicht möglich. Hierfür wird ein Modell für
den Kurs des zugrundeliegenden Finanzinstruments (Aktie, Devise,
...) gebraucht, bei dem es sich in aller Regel um einen
stochastischen Prozess in diskreter oder stetiger Zeit handelt.
Prozesse in stetiger Zeit haben den Vorteil, dass sich mit ihnen
viele Problemstellungen leichter analytisch behandeln lassen.
Prozesse in diskreter Zeit betrachten wir vorerst nur als
Approximationen, mit denen sich leichter numerische Berechnungen
durchführen lassen. Im zweiten Teil des Buches werden sie als
eigenständige Modelle in der Finanzzeitreihenanalyse diskutiert.
ist damit aber nicht möglich. Hierfür wird ein Modell für
den Kurs des zugrundeliegenden Finanzinstruments (Aktie, Devise,
...) gebraucht, bei dem es sich in aller Regel um einen
stochastischen Prozess in diskreter oder stetiger Zeit handelt.
Prozesse in stetiger Zeit haben den Vorteil, dass sich mit ihnen
viele Problemstellungen leichter analytisch behandeln lassen.
Prozesse in diskreter Zeit betrachten wir vorerst nur als
Approximationen, mit denen sich leichter numerische Berechnungen
durchführen lassen. Im zweiten Teil des Buches werden sie als
eigenständige Modelle in der Finanzzeitreihenanalyse diskutiert.
![]() die einfache
stochastische Differentialgleichung
die einfache
stochastische Differentialgleichung
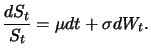
![]() im allgemeinen Modell (5.8) von der linearen
Form
im allgemeinen Modell (5.8) von der linearen
Form
![]() der geometrischen Brownschen Bewegung in
bestimmten Situationen, aber der Black-Scholes-Ansatz wird dennoch
als erste einfache Näherung zur Optionsbewertung benutzt. Die
prinzipielle Idee zur Ableitung von Optionspreisen lässt sich
außerdem auf allgemeinere Aktienkursmodelle übertragen.
der geometrischen Brownschen Bewegung in
bestimmten Situationen, aber der Black-Scholes-Ansatz wird dennoch
als erste einfache Näherung zur Optionsbewertung benutzt. Die
prinzipielle Idee zur Ableitung von Optionspreisen lässt sich
außerdem auf allgemeinere Aktienkursmodelle übertragen.
![]() , typischerweise dem
Fälligkeitstermin der Option, wertgleich sind. Dann folgt aus
der Annahme eines perfekten Marktes und insbesondere aus der
Arbitragefreiheit die Wertgleichheit zu jedem früheren
Zeitpunkt. Hierfür gibt es zwei äquivalente Möglichkeiten,
die wir am Beispiel eines Calls auf eine Aktie mit Kurs
, typischerweise dem
Fälligkeitstermin der Option, wertgleich sind. Dann folgt aus
der Annahme eines perfekten Marktes und insbesondere aus der
Arbitragefreiheit die Wertgleichheit zu jedem früheren
Zeitpunkt. Hierfür gibt es zwei äquivalente Möglichkeiten,
die wir am Beispiel eines Calls auf eine Aktie mit Kurs ![]() erläutern:
erläutern:
![]() gesetzt
werden, da ihre Anzahl frei wählbar ist. Zur Zeit
gesetzt
werden, da ihre Anzahl frei wählbar ist. Zur Zeit ![]() bestehen die beiden Portfolios aus
bestehen die beiden Portfolios aus
![]() auf ein
zugrundeliegendes Objekt mit Kurs
auf ein
zugrundeliegendes Objekt mit Kurs ![]() anwenden, wenn
anwenden, wenn ![]() eine
geometrische Brownsche Bewegung ist und wenn der Preis
eine
geometrische Brownsche Bewegung ist und wenn der Preis ![]() des
Derivats bis zu seiner Ausübung nur eine Funktion des aktuellen
Kurses und der Zeit ist:
des
Derivats bis zu seiner Ausübung nur eine Funktion des aktuellen
Kurses und der Zeit ist:
![]() . Dann existiert nach dem
folgenden Satz ein das Finanzinstrument duplizierendes Portfolio
und der obige Ansatz 1. ist auf die Preisbestimmung anwendbar. Bei
allgemeinen Derivaten muss das Duplikationsportfolio nicht nur zum
Ausübungszeitpunkt
. Dann existiert nach dem
folgenden Satz ein das Finanzinstrument duplizierendes Portfolio
und der obige Ansatz 1. ist auf die Preisbestimmung anwendbar. Bei
allgemeinen Derivaten muss das Duplikationsportfolio nicht nur zum
Ausübungszeitpunkt ![]() denselben Wert haben, sondern auch
vorher schon denselben Cashflow, d.h. dieselben
entnehmbaren Erträge oder zuzuschießenden Kosten, wie das
Derivat generieren. Die Existenz eines perfekten Hedge-Portfolios
als Grundlage von Ansatz 2. kann analog gezeigt werden.
denselben Wert haben, sondern auch
vorher schon denselben Cashflow, d.h. dieselben
entnehmbaren Erträge oder zuzuschießenden Kosten, wie das
Derivat generieren. Die Existenz eines perfekten Hedge-Portfolios
als Grundlage von Ansatz 2. kann analog gezeigt werden.
![]() Aktien und aus
Aktien und aus
![]() Zerobonds mit Fälligkeit
Zerobonds mit Fälligkeit ![]() und
Nominalwert
und
Nominalwert ![]() .
.
![]() des Portfolios in einem kleinen Zeitraum
des Portfolios in einem kleinen Zeitraum ![]() ändert. Dabei
schreiben wir
ändert. Dabei
schreiben wir
![]() usw.
usw.
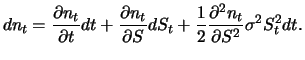
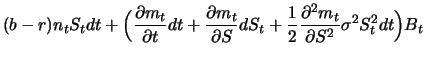
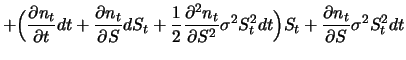
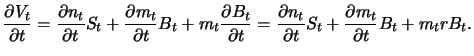
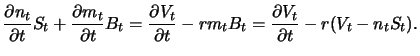
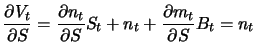
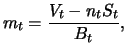
![]() im
Land der Fremdwährung gegeben ist. Die Bestandshaltekosten
im
Land der Fremdwährung gegeben ist. Die Bestandshaltekosten ![]() entsprechen der Differenz der Zinsen im Inland und im Land
der Fremdwährung: Kauft der Investor die Fremdwährung
vorzeitig, so kann er sein Kapital nicht mehr im Inland anlegen
und verliert den Zinssatz
entsprechen der Differenz der Zinsen im Inland und im Land
der Fremdwährung: Kauft der Investor die Fremdwährung
vorzeitig, so kann er sein Kapital nicht mehr im Inland anlegen
und verliert den Zinssatz ![]() , gewinnt dafür aber den Zinssatz
, gewinnt dafür aber den Zinssatz
![]() , den er für die Fremdwährung in deren Herkunftsland
erhält. Der Wert der Devisenoption ergibt
sich dann durch Lösen der Differentialgleichung (6.3)
von Black und Scholes mit der passenden, durch den Typ der Option
bestimmten Randbedingung.
, den er für die Fremdwährung in deren Herkunftsland
erhält. Der Wert der Devisenoption ergibt
sich dann durch Lösen der Differentialgleichung (6.3)
von Black und Scholes mit der passenden, durch den Typ der Option
bestimmten Randbedingung.