Generalized linear models (GLM) extend the concept of the
widely used linear regression model. The linear model
assumes that the response ![]() (the dependent variable) is equal to a
linear combination
(the dependent variable) is equal to a
linear combination
![]() and a normally distributed error term:
and a normally distributed error term:
Nelder & Wedderburn (1972) introduced the term
generalized linear models (GLM). A good resource
of material on this model is the monograph of
McCullagh & Nelder (1989).
The essential feature of the GLM is that the regression
function, i.e. the expectation
![]() of
of ![]() is a monotone function of the index
is a monotone function of the index
![]() . We denote the function which relates
. We denote the function which relates
![]() and
and ![]() by
by ![]() :
:
In the GLM framework we assume that the distribution of ![]() is a member of the exponential family. The exponential
family covers a broad range of distributions, for example discrete
as the Bernoulli or Poisson distribution and continuous as
the Gaussian (normal) or Gamma distribution.
is a member of the exponential family. The exponential
family covers a broad range of distributions, for example discrete
as the Bernoulli or Poisson distribution and continuous as
the Gaussian (normal) or Gamma distribution.
A distribution is said to be a member of the exponential family
if its probability function (if ![]() discrete) or its density
function (if
discrete) or its density
function (if ![]() continuous) has the structure
continuous) has the structure
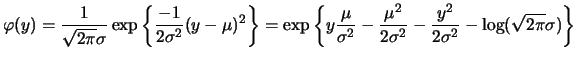
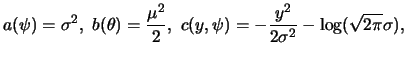
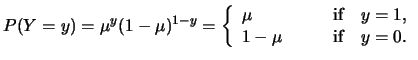
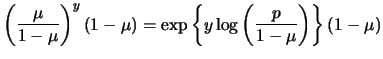 |
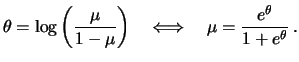
It is known that the least squares estimator
![]() in the classical linear model is also the maximum-likelihood
estimator for normally distributed errors.
By imposing that the distribution of
in the classical linear model is also the maximum-likelihood
estimator for normally distributed errors.
By imposing that the distribution of ![]() belongs to the exponential
family it is possible to stay in the framework of
maximum-likelihood for the GLM.
Moreover, the use of the general concept of exponential families has the
advantage that we can derive properties of different distributions
at the same time.
belongs to the exponential
family it is possible to stay in the framework of
maximum-likelihood for the GLM.
Moreover, the use of the general concept of exponential families has the
advantage that we can derive properties of different distributions
at the same time.
To derive the maximum-likelihood algorithm
in detail, we need to present some more
properties of the probability function or density function
![]() .
First of all,
.
First of all, ![]() is a density (w.r.t. the Lebesgue measure in the
continuous and w.r.t. the counting measure in the discrete case).
This allows us to write
is a density (w.r.t. the Lebesgue measure in the
continuous and w.r.t. the counting measure in the discrete case).
This allows us to write

| 0 | 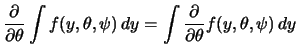 |
||
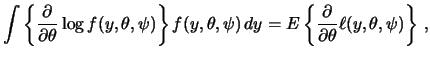 |
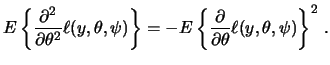
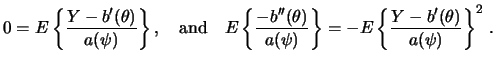
Apart from the distribution of ![]() , the link function
, the link function ![]() is another important part of the GLM. Recall the notation
is another important part of the GLM. Recall the notation
What link functions can we choose apart from the canonical?
For most of the models a number of special link functions exist.
For binomial ![]() for example, the logistic or Gaussian link functions
are often used. Recall that a binomial model with the canonical
logit link is called logit model. If the binomial distribution
is combined with the Gaussian link, it is called probit
model. A further alternative for binomial
for example, the logistic or Gaussian link functions
are often used. Recall that a binomial model with the canonical
logit link is called logit model. If the binomial distribution
is combined with the Gaussian link, it is called probit
model. A further alternative for binomial ![]() is the complementary log-log link
is the complementary log-log link
A very flexible class of link functions is the class of power functions which are also called Box-Cox transformations (Box & Cox, 1964). They can be defined for all models for which we have observations with positive mean. This family is usually specified as
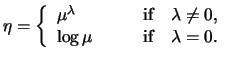
| Notation | Range | Canonical | Variance | ||||
| of |
|
|
link
|
|
|
||
|
Bernoulli
|
|
|
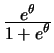
|
logit |
|
1 | |
|
Binomial
|
integer
|
|
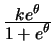
|
|
|
1 | |
|
Poisson
|
integer
|
|
|
|
|
1 | |
|
Negative
Binomial |
integer
|
|
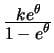
|
|
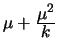
|
1 | |
|
Normal
|
|
|
|
identity | 1 | |
|
|
Gamma
|
|
|
|
reciprocal | |
|
|
|
Inverse
Gaussian |
|
|
|
squared
reciprocal
|
|
|
|
As already pointed out, the estimation method of choice for a GLM
is maximizing the likelihood function with respect to
![]() .
Suppose that we have the vector of
observations
.
Suppose that we have the vector of
observations
![]() and denote their expectations (given
and denote their expectations (given
![]() ) by
the vector
) by
the vector
![]() .
More precisely, we have
.
More precisely, we have
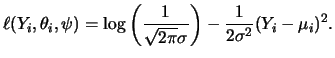
Let us remark that in the case where the distribution of
![]() itself is unknown, but its two first moments
can be specified, then the
quasi-likelihood
may replace
the log-likelihood (5.14). This means we assume that
itself is unknown, but its two first moments
can be specified, then the
quasi-likelihood
may replace
the log-likelihood (5.14). This means we assume that
Alternatively to the log-likelihood the deviance is used often. The deviance function is defined as
Before deriving the algorithm to determine
![]() , let us
have a look at (5.15) again. From
, let us
have a look at (5.15) again. From
![]() and (5.13) we see
and (5.13) we see
We will now maximize (5.21) w.r.t.
![]() .
For that purpose
take the first derivative of (5.21). This yields
the gradient
.
For that purpose
take the first derivative of (5.21). This yields
the gradient
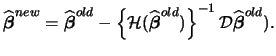
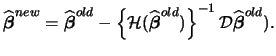
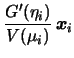 |
|||
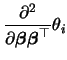 |
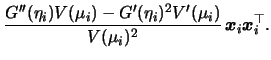 |
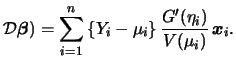
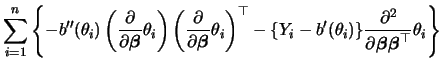 |
|||
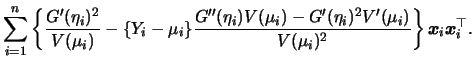 |
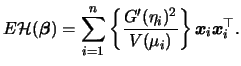
For the sake of simplicity let us concentrate on the Fisher scoring for the moment. Define the weight matrix
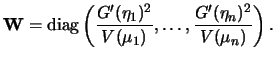
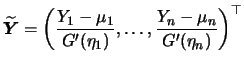
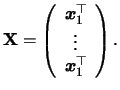
We see that each iteration step (5.23)
is the result of a weighted
least squares regression on the adjusted variables ![]() on
on
![]() . Hence, a GLM can be estimated by iteratively
reweighted least squares (IRLS).
Note further that in the linear regression model,
where we have
. Hence, a GLM can be estimated by iteratively
reweighted least squares (IRLS).
Note further that in the linear regression model,
where we have
![]() and
and
![]() ,
no iteration is necessary.
The Newton-Raphson algorithm can be given in a
similar way (with the more complicated weights and a
different formula for the adjusted variables).
There are several remarks on the algorithm:
,
no iteration is necessary.
The Newton-Raphson algorithm can be given in a
similar way (with the more complicated weights and a
different formula for the adjusted variables).
There are several remarks on the algorithm:
Additionally we have
The resulting estimator
![]() has an
asymptotic normal distribution, except of course for the standard
linear regression case with normal errors where
has an
asymptotic normal distribution, except of course for the standard
linear regression case with normal errors where
![]() has
an exact normal distribution.
has
an exact normal distribution.
The asymptotic covariance of the coefficient
![]() can be estimated by
can be estimated by
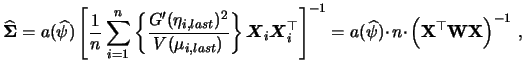
Recall that the economic model is based on the idea that a person will migrate if the utility (wage differential) exceeds the costs of migration. Of course neither one of the variables, wage differential and costs, are directly available. It is obvious that age has an important influence on migration intention. Younger people will have a higher wage differential. A currently low household income and unemployment will also increase a possible gain in wage after migration. On the other hand, the presence of friends or family members in the Western part of Germany will reduce the costs of migration. We also consider a city size indicator and gender as interesting variables (Table 5.1).
| Coefficients | ||
| constant | 0.512 | 2.39 |
| FAMILY/FRIENDS | 0.599 | 5.20 |
| UNEMPLOYED | 0.221 | 2.31 |
| CITY SIZE | 0.311 | 3.77 |
| FEMALE | -0.240 | -3.15 |
| AGE | -4.69
|
-14.56 |
| INCOME | 1.42
|
2.73 |
Now, we are interested in estimating the probability
of migration in dependence of the explanatory variables
![]() .
Recall, that
.
Recall, that
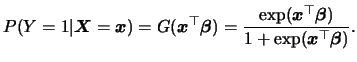
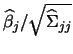 ).
).
For general aspects on semiparametric regression we refer to the textbooks of Pagan & Ullah (1999), Yatchew (2003), Ruppert et al. (1990). Comprehensive presentations of the generalized linear model can be found in Dobson (2001), McCullagh & Nelder (1989) and Hardin & Hilbe (2001). For a more compact introduction see Müller (2004), Venables & Ripley (2002, Chapter 7) and Gill (2000).
In the following notes, we give some references for topics we consider related to the considered models. References for specific models are listed in the relevant chapters later on.
The transformation model in (5.4) was first introduced in an econometric context by Box & Cox (1964). The discussion was revised many years later by Bickel & Doksum (1981). In a more recent paper, Horowitz (1996) estimates this model by considering a nonparametric transformation.
For a further reference of dimension reduction in nonparametric
estimation we mention projection pursuit and sliced
inverse regression. The projection pursuit algorithm is
introduced and investigated in detail in Friedman & Stuetzle (1981) and
Friedman (1987).
Sliced inverse regression means the estimation of
![]() where
where
![]() is the disturbance term and
is the disturbance term and ![]() the unknown
dimension of the model. Introduction and theory can be found e.g. in
Duan & Li (1991), Li (1991) or
Hsing & Carroll (1992).
the unknown
dimension of the model. Introduction and theory can be found e.g. in
Duan & Li (1991), Li (1991) or
Hsing & Carroll (1992).
More sophisticated models like censored or truncated dependent variables, models with endogenous variables or simultaneous equation systems (Maddala, 1983) will not be dealt with in this book. There are two reasons: On one hand the non- or semiparametric estimation of those models is much more complicated and technical than most of what we aim to introduce in this book. Here we only prepare the basics enabling the reader to consider more special problems. On the other hand, most of these estimation problems are rather particular and the treatment of them presupposes good knowledge of the considered problem and its solution in the parametric world. Instead of extending the book considerably by setting out this topic, we limit ourselves here to some more detailed bibliographic notes.
The non- and semiparametric literature on this is mainly separated into two directions, parametric modeling with unknown error distribution or modeling non-/semiparametrically the functional forms. In the second case a principal question is the identifiability of the model.
For an introduction to the problem of truncation, sample selection and limited dependent data, see Heckman (1976) and Heckman (1979). See also the survey of Amemiya (1984). An interesting approach was presented by Ahn & Powell (1993) for parametric censored selection models with nonparametric selection mechanism. This idea has been extended to general pairwise difference estimators for censored and truncated models in Honoré & Powell (1994). A mostly comprehensive survey about parametric and semiparametric methods for parametric models with non- or semiparametric selection bias can be found in Vella (1998). Even though implementation of and theory on these methods is often quite complicated, some of them turned out to perform reasonably well.
The second approach, i.e. relaxing the functional forms of the functions of interest, turned out to be much more complicated. To our knowledge, the first articles on the estimation of triangular simultaneous equation systems have been Newey et al. (1999) and Rodríguez-Póo et al. (1999), from which the former is purely nonparametric, whereas the latter considers nested simultaneous equation systems and needs to specify the error distribution for identifiability reasons. Finally, Lewbel & Linton (2002) found a smart way to identify nonparametric censored and truncated regression functions; however, their estimation procedure is quite technical. Note that so far neither their estimator nor the one of Newey et al. (1999) have been proved to perform well in practice.