5.1 Dimension Reduction

Researchers have looked for possible remedies, and a lot of effort has been allocated to developing methods which reduce the complexity of high dimensional regression problems. This refers to the reduction of dimensionality as well as allowance for partly parametric modeling. Not surprisingly, one follows the other. The resulting models can be grouped together as so-called semiparametric models.

All models that we will study in the following chapters can be motivated as generalizations of well-known parametric models, mainly of the linear model

$$E(Y\vert{\boldsymbol{X}}) = m({\boldsymbol{X}}) = {\boldsymbol{X}}^\top{\boldsymbol{\beta}}$$

or its generalized version

$$E(Y\vert{\boldsymbol{X}}) = m({\boldsymbol{X}}) = G\{ {\boldsymbol{X}}^\top{\boldsymbol{\beta}}\}\,.$$ (5.1)

Here $G$ denotes a known function, ${\boldsymbol{X}}$ is the $d$-dimensional vector of regressors and ${\boldsymbol{\beta}}$ is a coefficient vector that is to be estimated from observations for $Y$ and ${\boldsymbol{X}}$.

Let us take a closer look at model (5.1). This model is known as the generalized linear model. Its use and estimation are extensively treated in McCullagh & Nelder (1989). Here we give only some selected motivating examples.

What is the reason for introducing this functional $G$, called the link? (Note that other authors call its inverse $G^{-1}$ the link.) Clearly, if $G$ is the identity we are back in the classical linear model. As a first alternative let us consider a quite common approach for investigating growth models. Here, the model is often assumed to be multiplicative instead of additive, i.e.

$$Y = \prod_{j=1}^d X_j^{\beta_j} \cdot \varepsilon, \quad E\log(\varepsilon) = 0$$ (5.2)

in contrast to

$$Y = \prod_{j=1}^d X_j^{\beta_j} + \xi, \quad E\xi=0.$$ (5.3)

Depending on whether we have multiplicative errors $\varepsilon$ or additive errors $\xi$, we can transform model (5.2) to

$$E\{\log (Y) \vert{\boldsymbol{X}}\} = \sum_{j=1}^d \beta_j \log (X_j )$$ (5.4)

and model (5.3) to

$$E( Y \vert {\boldsymbol{X}}) = \exp \left\{ \sum_{j=1}^d \beta_j \log (X_j ) \right\} .$$ (5.5)

Considering now $\log ({\boldsymbol{X}})$ as the regressor instead of ${\boldsymbol{X}}$, equation (5.5) is equivalent to (5.1) with $G(\bullet) = \exp (\bullet)$. Equation (5.4), however, is a transformed model, see the bibliographic notes for references on this model family.

The most common cases in which link functions are used are binary responses ( $Y\in \{ 0,1 \}$) or multicategorical ( $Y\in \{ 0,1,\ldots ,J \}$) responses and count data ($Y \sim$ Poisson). For the binary case, let us introduce an example that we will study in more detail in Chapters 7 and 9.

Table 5.1: Descriptive statistics for migration data, $n=3235$

		Yes	No	(in %)
$Y$	MIGRATION INTENTION	38.5	61.5
$X_1$	FAMILY/FRIENDS IN WEST	85.6	11.2
$X_2$	UNEMPLOYED/JOB LOSS CERTAIN	19.7	78.9
$X_3$	CITY SIZE 10,000-100,000	29.3	64.2
$X_4$	FEMALE	51.1	49.8
		Min	Max	Mean	S.D.
$X_5$	AGE (in years)	18	65	39.84	12.61
$X_6$	HOUSEHOLD INCOME (in DM)	200	4000	2194.30	752.45

EXAMPLE 5.1  
Imagine we are interested in possible determinants of the migration decision of East Germans to leave the East for West Germany. Think of $Y^*$ as being the net-utility from migrating from the eastern part of Germany to the western part. Utility itself is not observable but we can observe characteristics of the decision makers and the alternatives that affect utility. As $Y^*$ is not observable it is called a latent variable. Let the observable characteristics be summarized in a vector ${\boldsymbol{X}}$. This vector ${\boldsymbol{X}}$ may contain variables such as education, age, sex and other individual characteristics. A selection of such characteristics is shown in Table 5.1. $\Box$

In Example 5.1, we hope that the vector of regressors ${\boldsymbol{X}}$ captures the variables that systematically affect each person's utility whereas unobserved or random influences are absorbed by the term $\varepsilon$. Suppose further, that the components of ${\boldsymbol{X}}$ influence net-utility through a multivariate function $v(\bullet)$ and that the error term is additive. Then the latent-variable model is given by

$$Y^*=v({\boldsymbol{X}})-\varepsilon \quad\textrm{ and }\quad Y=\l... ... \quad \textrm{ if }Y^*>0, \\ 0 \quad \textrm{ otherwise. } \end{array} \right.$$ (5.6)

Hence, what we really observe is the binary variable $Y$ that takes on the value 1 if net-utility is positive (person intends to migrate) and 0 otherwise (person intends to stay). Then some calculations lead to

$$P(Y=1 \mid {\boldsymbol{X}}={\boldsymbol{x}}) = E(Y \mid {\boldsy... ...{\boldsymbol{x}}) = G_{\varepsilon\vert{\boldsymbol{x}}}\{v({\boldsymbol{x}})\}$$ (5.7)

with $G_{\varepsilon\vert x}$ being the cdf of $\varepsilon$ conditional on ${\boldsymbol{x}}$.

Recall that standard parametric models assume that $\varepsilon$ is independently distributed of ${\boldsymbol{X}}$ with known distribution function $G_{\varepsilon\vert{\boldsymbol{x}}}=G$, and that the index $v(\bullet)$ has the following simple form:

$$v({\boldsymbol{x}}) = \beta_{0} + {\boldsymbol{x}}^\top{\boldsymbol{\beta}}.$$ (5.8)

The most popular distribution assumptions regarding the error are the normal and the logistic ones, leading to the so-called probit or logit models with $G (\bullet )=\Phi (\bullet )$ (Gaussian cdf), respectively $G (\bullet )=\exp (\bullet) / \{1+\exp (\bullet)\}$. We will learn how to estimate the coefficients $\beta_{0}$ and ${\boldsymbol{\beta}}$ in Section 5.2.

The binary choice model can be easily extended to the multicategorical case, which is usually called discrete choice model. We will not discuss extensions for multicategorical responses here. Some references for these models are mentioned in the bibliographic notes.

Several approaches have been proposed to reduce dimensionality or to generalize parametric regression models in order to allow for nonparametric relationships. Here, we state three different approaches:

• variable selection in nonparametric regression,
• generalization of (5.1) to a nonparametric link function,
• generalization of (5.1) to a semi- or nonparametric index,

which are discussed in more detail.

5.1.1 Variable Selection in Nonparametric Regression

The intention of variable selection is to choose an appropriate subset of variables, ${\boldsymbol{X}}_r=(X_{j_1},\ldots,X_{j_r})^\top \in {\boldsymbol{X}}=(X_{1},\ldots,X_{d})^\top$, from the set of all variables that could potentially enter the regression. Of course, the selection of the variables could be determined by the particular problem at hand, i.e. we choose the variables according to insights provided by some underlying economic theory. This approach, however, does not really solve the statistical side of our modeling process. The curse of dimensionality could lead us to keep the number of variables as low as possible. On the other hand, fewer variables could in turn reduce the explanatory power of the model. Thus, after having chosen a set of variables on theoretical grounds in a first step, we still do not know how many and, more importantly, which of these variables will lead to optimal regression results. Therefore, a variable selection method is needed that uses a statistical selection criterion.

Vieu (1994) has proposed to use the integrated square error $\ise$ to measure the quality of a given subset of variables. In theory, a subset of variables is defined to be an optimal subset if it minimizes the integrated squared error:

$$\ise({\boldsymbol{X}}_r^{opt})=\min_{{\boldsymbol{X}}_r} \ise({\boldsymbol{X}}_r)$$

where ${\boldsymbol{X}}_r \subset {\boldsymbol{X}}$. In practice, the $\ise$ is replaced by its sample analog, the multivariate analog of the cross validation function (3.38). After the variables have been selected, the conditional expectation of $Y$ on ${\boldsymbol{X}}_r$ is calculated by some kind of standard nonparametric multivariate regression technique such as the kernel regression estimator.

5.1.2 Nonparametric Link Function

Index models play an important role in econometrics. An index is a summary of different variables into one number, e.g. the price index, the growth index, or the cost-of-living index. It is clear that by summarizing all the information contained in the variables $X_{1},\ldots,X_{d}$ into one ``single index'' term we will greatly reduce the dimensionality of a problem. Models based on such an index are known as single index models (SIM). In particular we will discuss single index models of the following form:

$$E(Y\vert{\boldsymbol{X}})=m({\boldsymbol{X}})=g\left\{ v_{\boldsymbol{\beta}}({\boldsymbol{X}}) \right\},$$ (5.9)

where $g(\bullet)$ is an unknown link function and $v_{\boldsymbol{\beta}}(\bullet)$ an up to ${\boldsymbol{\beta}}$ specified index function. The estimation can be carried out in two steps. First, we estimate ${\boldsymbol{\beta}}$. Then, using the index values for our observations, we can estimate $g$ by nonparametric regression. Note that estimating $g(\bullet)$ by regressing the $Y$ on $v_{\widehat{{\boldsymbol{\beta}}}}( {\boldsymbol{X}})$ is only a one-dimensional regression problem.

Obviously, (5.9) generalizes (5.7) in that we do not assume the link function $G$ to be known. For that purpose we replaced $G$ by $g$ to emphasize that the link function needs to be estimated. Notice, that often the general index function $v_{\boldsymbol{\beta}}({\boldsymbol{X}})$ is replaced by the linear index ${\boldsymbol{X}}^\top{\boldsymbol{\beta}}$. Equations (5.5) and (5.6) together with (5.8) give examples for such linear index functions.

5.1.3 Semi- or Nonparametric Index

In many applications a canonical partitioning of the explanatory variables exists. In particular, if there are categorical or discrete explanatory variables we may want to keep them separate from the other design variables. Note that only the continuous variables in the nonparametric part of the model cause the curse of dimensionality (Delgado & Mora, 1995). In the following chapters we will study the following models:

• Additive Model (AM)
  The standard additive model is a generalization of the multiple linear regression model by introducing one-dimensional nonparametric functions in the place of the linear components. Here, the conditional expectation of $Y$ given ${\boldsymbol{X}}=(X_1,\ldots ,X_d)^\top$ is assumed to be the sum of unknown functions of the explanatory variables plus an intercept term:

  $$E(Y\vert{\boldsymbol{X}})=c + \sum_{j=1}^d g_j(X_j)$$ (5.10)

  
  
  Observe how reduction is achieved in this model: Instead of estimating one function of several variables, as we do in completely nonparametric regression, we merely have to estimate $d$ functions of one-dimensional variables $X_j$.
• Partial Linear Model (PLM)
  Suppose we only want to model parts of the index linearly. This could be for analytical reasons or for reasons going back to economic theory. For instance, the impact of a dummy variable $X_1 \in \{ 0,1 \}$ might be sufficiently explained by estimating the coefficient $\beta_1$.

  For the sake of clarity, let us now separate the $d$-dimensional vector of explanatory variables into ${\boldsymbol{U}}=(U_1,\ldots, U_p)^\top$ and ${\boldsymbol{T}}=(T_1,\ldots, T_q)^\top$. The regression of $Y$ on ${\boldsymbol{X}}=({\boldsymbol{U}},{\boldsymbol{T}})$ is assumed to have the form:

  $$E(Y\vert{\boldsymbol{U}},{\boldsymbol{T}})={\boldsymbol{U}}^\top {\boldsymbol{\beta}}+ m({\boldsymbol{T}})$$ (5.11)

  
  
  where $m(\bullet)$ is an unknown multivariate function of the vector ${\boldsymbol{T}}$. Thus, a partial linear model can be interpreted as a sum of a purely parametric part, ${\boldsymbol{U}}^\top{\boldsymbol{\beta}}$, and a purely nonparametric part, $m({\boldsymbol{T}})$. Not surprisingly, estimating ${\boldsymbol{\beta}}$ and $m(\bullet)$ involves the combination of both parametric and nonparametric regression techniques.
• Generalized Additive Model (GAM)
  Just like the (standard) additive model, generalized additive models are based on the sum of $d$ nonparametric functions of the $d$ variables ${\boldsymbol{X}}$ (plus an intercept term). In addition, they allow for a known parametric link function, $G(\bullet)$, that relates the sum of functions to the dependent variable:

  $$E(Y\vert{\boldsymbol{X}})=G \left\{c + \sum_{j=1}^d g_j(X_j) \right\}\,.$$ (5.12)

  
  

• Generalized Partial Linear Model (GPLM)
  Introducing a link $G(\bullet)$ for a partial linear model ${\boldsymbol{U}}^\top{\boldsymbol{\beta}}+ m({\boldsymbol{T}})$ yields the generalized partial linear model (GPLM):
  $$E (Y\vert{\boldsymbol{U}},{\boldsymbol{T}}) = G \left\{ {\boldsymbol{U}}^\top {\boldsymbol{\beta}}+m({\boldsymbol{T}})\right\}.$$
  $G$ denotes a known link function as in the GAM. In contrast to the GAM, $m(\bullet)$ is possibly a multivariate nonparametric function of the variable ${\boldsymbol{T}}$.
• Generalized Partial Linear Partial Additive Model (GAPLM)
  In high dimensions of ${\boldsymbol{T}}$ the estimate of the nonparametric function $m(\bullet)$ in the GPLM faces the same problems as the fully nonparametric multidimensional regression function estimates: the curse of dimensionality and the practical problem of interpretability. Hence, it is useful to think about a lower dimensional modeling of the nonparametric part. This leads to the GAPLM with an additive structure in the nonparametric component:
  $$E (Y\vert{\boldsymbol{U}},{\boldsymbol{T}}) = G \left\{ {\boldsymbol{U}}^\top {\boldsymbol{\beta}}+ \sum_{j=1}^q g_{j}(T_{j}) \right\}.$$
  Here, the $g_{j}(\bullet)$ will be univariate nonparametric functions of the variables $T_{j}$. In the case of an identity function $G$ we speak of an additive partial linear model (APLM)

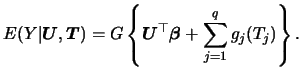
More discussion and motivation is given in the following chapters where the different models are discussed in detail and the specific estimation procedures are presented. Before proceeding with this task, however, we will first introduce some facts about the parametric generalized linear model (GLM). The following section is intended to give more insight into this model since its concept and the technical details of its estimation will be necessary for its semiparametric modification in Chapters 6 to 9.