We have still not found a way to select the bandwidth that is both applicable in practice as well as theoretically desirable. In the following two subsections we will introduce two of the most frequently used methods of bandwidth selection, the plug-in method and the method of cross-validation. The treatments of both methods will describe one representative of each method. In the case of the plug-in method we will focus on the ``quick & dirty" plug-in method introduced by Silverman. With regard to cross-validation we will focus on least squares cross-validation. For more complete treatments of plug-in and cross-validation methods of bandwidth selection, see e.g. Härdle (1991) and Park & Turlach (1992).
Generally speaking, plug-in methods derive their name from their
underlying principle: if you have an expression involving an
unknown parameter, replace the unknown parameter with an estimate.
Take (3.19) as an example. The
expression on the right hand side involves the unknown quantity
![]() .
Suppose we knew or assumed that the unknown density
.
Suppose we knew or assumed that the unknown density ![]() belongs to the family of normal distributions with mean
belongs to the family of normal distributions with mean ![]() and
variance
and
variance
![]() then we have
then we have
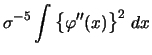 |
(3.21) | ||
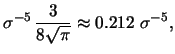 |
(3.22) |
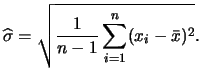
You may object by referring to what we said at the beginning of
Chapter 2. Isn't assuming normality of ![]() just the opposite of the philosophy of nonparametric density
estimation? Yes, indeed. If we knew that
just the opposite of the philosophy of nonparametric density
estimation? Yes, indeed. If we knew that ![]() had a normal distribution
then we could estimate its density much easier and more efficiently
if we simply estimate
had a normal distribution
then we could estimate its density much easier and more efficiently
if we simply estimate ![]() with the sample mean and
with the sample mean and
![]() with the sample variance, and plug these estimates into
the formula of the normal density.
with the sample variance, and plug these estimates into
the formula of the normal density.
What we achieved by working under the normality assumption is an explicit,
applicable formula for bandwidth selection. In practice, we do not know
whether ![]() is normally distributed. If it is, then
is normally distributed. If it is, then
![]() in
(3.24) gives the optimal bandwidth. If not, then
in
(3.24) gives the optimal bandwidth. If not, then
![]() in (3.24) will give a bandwidth not too far from the
optimum if the distribution of
in (3.24) will give a bandwidth not too far from the
optimum if the distribution of ![]() is not too different from the normal
distribution (the ``reference distribution'').
That's why we refer to (3.24) as a rule-of-thumb
bandwidth that will give reasonable results for all distributions that are
unimodal, fairly symmetric and do not have tails that are too fat.
is not too different from the normal
distribution (the ``reference distribution'').
That's why we refer to (3.24) as a rule-of-thumb
bandwidth that will give reasonable results for all distributions that are
unimodal, fairly symmetric and do not have tails that are too fat.
A practical problem with the rule-of-thumb bandwidth is
its sensitivity to outliers.
A single outlier may cause a too large estimate of ![]() and hence
implies a too large bandwidth.
A more robust
estimator is obtained from the interquartile range
and hence
implies a too large bandwidth.
A more robust
estimator is obtained from the interquartile range
| (3.25) |
| (3.26) | |||
As mentioned earlier, we will focus on least squares cross-validation.
To get started, consider an alternative distance measure between
![]() and
and ![]() , the integrated squared error (
, the integrated squared error (![]() ):
):
If we look at this term more closely,
we observe that
![]() is the expected value
of
is the expected value
of
![]() , where the expectation is calculated
w.r.t. an independent random variable
, where the expectation is calculated
w.r.t. an independent random variable ![]() .
We can estimate this expected value by
.
We can estimate this expected value by
Let us repeat the formula of the
integrated squared error (![]() ), the criterion function we seek to
minimize with respect to
), the criterion function we seek to
minimize with respect to ![]() :
:
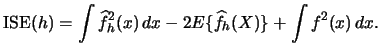 |
(3.34) |
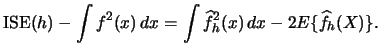 |
(3.35) |
A nice feature of the cross-validation method is that the selected
bandwidth automatically adapts to the smoothness of
![]() .
This is in contrast to plug-in methods like Silverman's rule-of-thumb
or the refined methods presented in Subsection 3.3.3. Moreover,
the cross-validation principle can analogously be applied to other
density estimators (different from the kernel method). We will also see
these advantages later in the context of regression function estimation.
.
This is in contrast to plug-in methods like Silverman's rule-of-thumb
or the refined methods presented in Subsection 3.3.3. Moreover,
the cross-validation principle can analogously be applied to other
density estimators (different from the kernel method). We will also see
these advantages later in the context of regression function estimation.
Finally, it can be shown that the bandwidth selected by minimizing
![]() fulfills an optimality property.
Denote the bandwidth selected by the cross-validation criterion by
fulfills an optimality property.
Denote the bandwidth selected by the cross-validation criterion by
![]() and assume that the density
and assume that the density ![]() is a bounded
function. Stone (1984) proved that this bandwidth
is asymptotically optimal in the following sense
is a bounded
function. Stone (1984) proved that this bandwidth
is asymptotically optimal in the following sense
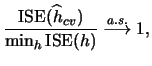
With Silverman's rule-of-thumb we introduced in Subsection 3.3.1
the simplest possible plug-in bandwidth. Recall that essentially
we assumed a normal density for a simple calculation of ![]() .
This procedure yields a relatively good estimate of the optimal
bandwidth if the true density function
.
This procedure yields a relatively good estimate of the optimal
bandwidth if the true density function ![]() is nearly normal.
However, if this is not the case (as for multimodal densities)
Silverman's rule-of-thumb will fail dramatically.
A natural refinement consists of using nonparametric estimates
for
is nearly normal.
However, if this is not the case (as for multimodal densities)
Silverman's rule-of-thumb will fail dramatically.
A natural refinement consists of using nonparametric estimates
for ![]() as well. A further refinement is the use of a better
approximation to
as well. A further refinement is the use of a better
approximation to
![]() . The following approaches apply these ideas.
. The following approaches apply these ideas.
In contrast to the cross-validation method plug-in bandwidth
selectors try to find a bandwidth that minimizes ![]() . This
means we are looking at another optimality criteria than these
from the previous section.
. This
means we are looking at another optimality criteria than these
from the previous section.
A common method
of assessing the quality of a selected bandwidth
![]() is to compare it with
is to compare it with ![]() , the
, the ![]() optimal bandwidth,
in relative value. We say that the convergence of
optimal bandwidth,
in relative value. We say that the convergence of
![]() to
to ![]() is of order
is of order
![]() if
if
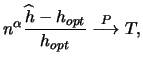
Park & Marron (1990) proposed
to estimate
![]() in
in ![]() by using a nonparametric estimate
of
by using a nonparametric estimate
of ![]() and taking the second derivative from this estimate. Suppose we use a bandwidth
and taking the second derivative from this estimate. Suppose we use a bandwidth ![]() here, then the second derivative of
here, then the second derivative of
![]() can be computed as
can be computed as
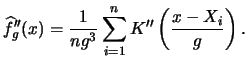
In Subsection 3.3.2 we introduced
Most of the other existing bandwidth choice methods attempt to minimize ![]() .
A condition analogous
to (3.41) for
.
A condition analogous
to (3.41) for ![]() is usually much more complicated to
prove. Hence, most of the literature
is concerned with investigating the relative rate of convergence
of a selected bandwidth
is usually much more complicated to
prove. Hence, most of the literature
is concerned with investigating the relative rate of convergence
of a selected bandwidth
![]() to
to ![]() .
Fan & Marron (1992)
derived a Fisher-type lower bound
for the relative errors of a bandwidth selector. It is given by
.
Fan & Marron (1992)
derived a Fisher-type lower bound
for the relative errors of a bandwidth selector. It is given by
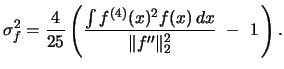
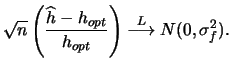
The biased cross validation method of Hall et al. (1991)
has this property, however, this selector
is only superior for very large samples.
Another ![]() -convergent method is the smoothed cross-validation method
but this selector pays with a larger asymptotic variance.
-convergent method is the smoothed cross-validation method
but this selector pays with a larger asymptotic variance.
In summary: one best method does not exist! Moreover,
even asymptotically
optimal criteria may show bad behavior in simulations. See the
bibliographic notes for references on such simulation studies.
As a consequence, we recommend determining bandwidths by
different selection methods and comparing the resulting
density estimates.