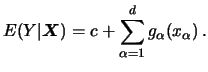9. Generalized Additive Models

In Chapter 8 we discussed additive models (AM) of the form

$$E(Y\vert {\boldsymbol{X}}) = c + \sum_{\alpha =1}^d g_\alpha ( x_\alpha )\,.$$ (9.1)

Note that we put $EY=c$ and $E\{g_\alpha (X_\alpha)\}=0$ for identification.

In this chapter we discuss variants of the model (9.1). Recall that the main advantage of an additive model is that (compared to a fully nonparametric model) it avoids the curse of dimensionality and that the component functions are easy to interpret. Stone (1986) proved that this also holds for generalized additive models.

We will focus here on the modification of (9.1) by additional parametric, in particular linear, components. The resulting additive partial linear model (APLM) can be written as

$$E(Y\vert {\boldsymbol{U}}, {\boldsymbol{T}}) = c+ {\boldsymbol{U}}^\top \beta + \sum_{\alpha =1}^q g_\alpha ( T_\alpha )\,,$$ (9.2)

where we again use the partitioning ${\boldsymbol{X}}=({\boldsymbol{U}},{\boldsymbol{T}})$ introduced in Chapter 7. Moreover, we will extend AM and APLM by a possibly nontrivial link function $G$. This leads to the generalized additive model (GAM)

$$E(Y\vert {\boldsymbol{X}}) = G \left\{ c+ \sum_{\alpha =1}^d g_\alpha ( X_\alpha ) \right\}$$ (9.3)

or to the generalized additive partial linear model (GAPLM)

$$E(Y\vert {\boldsymbol{U}}, {\boldsymbol{T}}) = G \left\{ c+{\boldsymbol{U}}^\top \beta + \sum_{\alpha =1}^q g_\alpha ( T_\alpha ) \right\} \,.$$ (9.4)

It is obvious that model (9.4) is a modification of the GPLM. Consequently we will base the estimation of the GAPLM to a significant extent on the estimation algorithms for the GPLM. In fact, most of the methodology introduced in this chapter comes from the combination of previously introduced techniques for GLM, GPLM, and AM. We will therefore frequently refer to the previous Chapters 5, 7 and 8.