8.2 Marginal Integration Estimator

We now turn to the problem of estimating the marginal effects of the regressors $X_\alpha$. The marginal effect of an explanatory variable tells how $Y$ changes on average if this variable is varying. In other words, the marginal effect represents the conditional expectation $E_{\varepsilon,{\boldsymbol{X}}_{\underline{\alpha}}}(Y\vert X_\alpha)$ where the expectation is not only taken on the error distribution but also on all other regressors. (Note, that we usually suppressed the $\varepsilon$ in all expectations up to now. This is the only case where we need to explicitely mention on which distribution the expectation is calculated.)

As already indicated, in case of true additivity the marginal effects correspond exactly to the additive component functions $g_\alpha$. The estimator here is based on an integration idea, coming from the following observation. Denote by $f_\alpha$ the marginal density of $X_\alpha$. We have from (8.2)

$$E_{X_\alpha} \{ g_\alpha (X_\alpha )\} = \int g_\alpha(t) f_\alpha (t)\, dt = 0, \quad \textrm{ for all }\ \alpha=1,\ldots ,d.$$

Denote further ${\boldsymbol{X}}_{\underline{\alpha}}$ the vector of all explanatory variables but $X_\alpha$, i.e.

$${\boldsymbol{X}}_{\underline{\alpha}} = \left( X_{i1},\ldots ,X_{i(\alpha -1)},X_{i(\alpha+1)},\ldots ,X_{id} \right)$$

and $f_{\underline{\alpha}}$ their joint pdf. If now $m({\boldsymbol{X}})=m(X_\alpha,{\boldsymbol{X}}_{\underline{\alpha}})$ is of additive form (8.1), then

$$\int m({\boldsymbol{x}}) f_{\underline{\alpha}}({\boldsymbol{x}}_{\underline{\alpha}}) \prod_{k \neq \alpha }dX_k = E_{{\boldsymbol{X}}_{\underline{\alpha}}} [ m(X_\alpha,{\boldsymbol{X}}_{\underline{\alpha}}) ]$$

$$= E_{{\boldsymbol{X}}_{\underline{\alpha}}} \{ c+g_\alpha (X_\alpha)+\sum_{k\neq \alpha} g_k (X_k) \}$$

$$= c+g_\alpha (X_\alpha ) \,.$$ (8.12)

You see that indeed we calculate $E_{\varepsilon,{\boldsymbol{X}}_{\underline{\alpha}}}(Y\vert X_\alpha)$ instead of $E_{\varepsilon}(Y\vert X_\alpha)$. We give a simple example to illustrate marginal integration:

EXAMPLE 8.3  
Suppose we have a data generating process of the form

$$Y = 4 + X_1^2 + 2\cdot \sin (X_2) + \varepsilon \,,$$

where $X_1 \sim U[-2,2]$ and $X_2 \sim U[-3,3]$ uniformly distributed and $\varepsilon$ a regular, possibly heteroscedastic noise term. The regression function obviously is

$$m(x_1,x_2) = E(Y\vert{\boldsymbol{X}}={\boldsymbol{x}}) = 4 + x_1^2 + 2\cdot \sin (x_2).$$

We have consequently marginal expectations

$$E_{X_2}\{m(X_1,X_2)\} = \int_{-3}^3 \frac{1}{6} \left\{ 4 + X_1^2 + 2\cdot \sin (u) \right\} du = 4 + X_1^2 \,,$$

$$E_{X_1}\{m(X_1,X_2)\} = \int_{-2}^2 \frac{1}{4} \left\{ 4 + u^2 + 2\cdot \sin (X_2) \right\} du = \frac{16}{3} + 2\cdot \sin (X_2)\,.$$

This yields the component functions

$$g_1 (x_1) =x_1^2-\frac 43\,,\quad g_2 (x_2)= 2 \sin (x_2)\,,\quad\textrm{and}\quad c=\frac{16}{3}\,$$

which are normalized to $E_{X_\alpha}g_\alpha(X_\alpha)=0$ $\Box$.

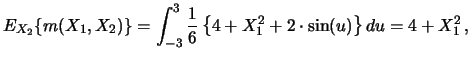
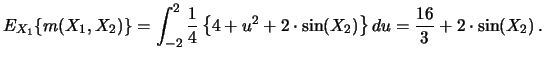
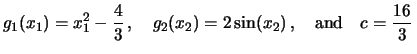
Many extensions and modifications of the integration approach have been developed recently. We consider now the simultaneous estimation of both the functions and their derivatives by combining the procedure with a local polynomial approach (Subsections 8.2.1, 8.2.2) and the estimation of interaction terms (Subsection 8.2.3).

8.2.1 Estimation of Marginal Effects

In order to estimate the marginal effect $g_\alpha (X_\alpha)$, equation (8.12) suggests the following idea: First estimate the function $m(\bullet)$ with a multidimensional pre-smoother $\widetilde{m}$ , then integrate out the variables different from $X_\alpha$. In the estimation procedure integration can be replaced by averaging (over the directions not of interest, i.e. ${\boldsymbol{X}}_{\underline{\alpha}}$) resulting in

$$\widehat{\left\{ g_\alpha (\bullet)+c \right\}} = \frac 1n \sum_{i=1}^n \widetilde{m}(\bullet,{\boldsymbol{X}}_{i\underline{\alpha}}) \ .$$ (8.13)

Note that to get the marginal effects, we just integrate $\widetilde{m}$ over all other (the nuisance) directions $\underline{\alpha}$. In case of additivity these marginal effects are the additive component functions $g_\alpha$ plus the constant $c$. As for backfitting, the constant $c$ can be estimated consistently by $\widehat{c} = \overline{Y}$ at $\sqrt{n}$-rate. Hence, a possible estimate for $g_\alpha$ is

$$\widehat{g}_\alpha (\bullet) = \frac 1n \sum_{i=1}^n \widetilde{m} (\bullet ,{\boldsymbol{X}}_{i\underline{\alpha}}) - \overline{Y}\,.$$ (8.14)

Centering the marginals yields the same asymptotic result, i.e.

$$\widehat{g}_\alpha (\bullet) = \widehat{ \left\{ g_\alpha (\bullet)+c \right\}} - \frac 1{n}\sum_{i=1}^n \widehat{ \left\{ g_\alpha (X_{i\alpha})+c \right\}}$$

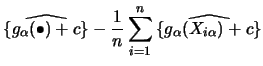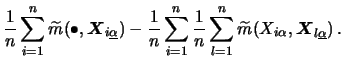$$= \frac 1n \sum_{i=1}^n \widetilde{m}(\bullet ,{\boldsymbol{X}}_{i\... ..._{l=1}^n \widetilde{m}(X_{i\alpha} ,{\boldsymbol{X}}_{l\underline{\alpha}}) \,.$$ (8.15)

It remains to discuss how to obtain a reasonable pre-estimator $\widetilde{m}(x_\alpha ,{\boldsymbol{x}}_{l\underline{\alpha}})$. Principally this could be any multivariate nonparametric estimator. We make use here of a special type of multidimensional local linear kernel estimators, cf. Ruppert & Wand (1994) and Severance-Lossin & Sperlich (1999). This estimator is given by minimizing

$${\sum_{i=1}^n \{ Y_i-\beta_0-\beta_1(X_{i\alpha}-x_\alpha )- \ldots -\beta_p (X_{i\alpha}-x_\alpha)^p \}^2}$$

$$\quad\quad\quad\quad \cdotp K_h(X_{i\alpha}-x_\alpha) {\mathcal{K... ...\boldsymbol{X}}_{i\underline{\alpha}} - {\boldsymbol{x}}_{l\underline{\alpha}})$$ (8.16)

w.r.t. to $\beta_0,\ldots,\beta_p$. Here, $K_h$ denotes a (scaled) univariate and ${\mathcal{K}}_{\mathbf{H}}$ a (scaled) $(d-1)$-dimensional kernel function. $h$ and ${\mathbf{H}}=\widetilde{h}{\mathbf{I}}_{d-1}$ are the bandwidth parameters. To obtain the estimated marginal function, we need to extract the estimated $\beta_0$. This means we use

$$\widetilde{m}(x_\alpha,{\boldsymbol{x}}_{l\underline{\alpha}}) ={... ...alpha )^{-1}{\mathbf{X}}^\top _\alpha {\mathbf{W}}_{l\alpha} {\boldsymbol{Y}},$$

where

$${\mathbf{W}}_{l\alpha} = \mathop{\hbox{diag}}\left(\left\{ \frac ... ...}} - {\boldsymbol{x}}_{l\underline{\alpha}}) \right\}_{i=1,\ldots,n}\right)\,,$$

$${\mathbf{X}}_\alpha =\left( \begin{array}{ccccc} 1 & X_{1\alpha }... ...{n\alpha}-x_\alpha)^2 & \ldots & (X_{n\alpha}-x_\alpha)^p \end{array}\right) .$$

This estimator is a local polynomial smoother of degree $p$ for the direction $\alpha$ and a local constant one for all other directions. Note that the resulting estimate is simply a weighted least squares estimate. For a more detailed discussion recall Subsection 4.1.3, where local polynomial estimators have been introduced. Bringing the estimate together, we have

$$\widehat{g}_\alpha (x_\alpha) = \frac 1n \sum_{l=1}^n {\boldsymbo... ...hbf{X}}^\top _\alpha {\mathbf{W}}_{l\alpha} {\boldsymbol{Y}} - \overline{Y} \ .$$ (8.17)

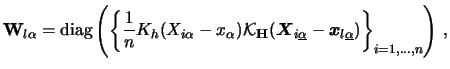
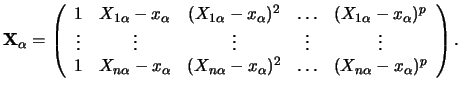
To derive asymptotic properties of these estimators the concept of equivalent kernels is used, see e.g. Ruppert & Wand (1994). The main idea is that the local polynomial smoother of degree $p$ is asymptotically equivalent (i.e. has the same leading term) to a kernel estimator using a higher order kernel given by

$$K^\star_\nu (u) = \sum^p_{t=0} s_{\nu t} u^t K(u),$$ (8.18)

where ${\mathbf{S}}=\left(\left( \int u^{t+r} K(u)\, du \right)_{0\leq t,r \leq p} \right)$ and ${\mathbf{S}}^{-1} =\left((s_{\nu t})_{0\leq \nu,t \leq p}\right)$. For the resulting asymptotics and some real data examples we refer to the following subsections.

8.2.2 Derivative Estimation for the Marginal Effects

We now extend the marginal integration method to the estimation of derivatives of the functions $g_\alpha(\bullet)$. For additive linear functions their first derivatives are constants and so all higher order derivatives vanish. However, very often in economics the derivatives of the marginal effects are of essential interest, e.g. to determine the elasticities or returns to scale as in Example 8.5.

To estimate the derivatives of the additive components, we do not need any further extension of our method, since using a local polynomial estimator of order $p$ for the pre-estimator $\widetilde{m}$ provides us simultaneously with both component functions and derivative estimates up to degree $p$. The reason is that the optimal $\beta_\nu$ in equation (8.16) is an estimate for $g_\alpha^{(\nu)}(X_\alpha ) / \nu !$, provided that dimension $\alpha$ is separable from the others. In case of additivity this is automatically given.

Thus, we can use

$$\widehat{g}_\alpha^{(\nu)} (x_\alpha) = \frac{\nu !}{n} \sum_{l=1... ...\alpha )^{-1} {\mathbf{X}}^\top _\alpha {\mathbf{W}}_{l\alpha} {\boldsymbol{Y}}$$ (8.19)

for estimating the $\nu$th derivative. Compare this with equation (8.17). Here, ${\boldsymbol{e}}_\nu$ is now the $(\nu+1)$th unit vector in order to extract the estimate for $\beta_\nu$ Asymptotic properties are derived in Severance-Lossin & Sperlich (1999). Recall that the integration estimator requires to choose two bandwidths, $h$ for the direction of interest and $\widetilde{h}$ for the nuisance direction.

THEOREM 8.3  
Consider kernels $K$ and ${\mathcal{K}}$, where ${\mathcal{K}}$ is a product of univariate kernels of order $q>2$, $h$, $\widetilde{h}$ bandwidths such that $nh\widetilde{h}^{(d-1)}/\log^2(n) \to \infty$, $\widetilde{h}^qh^{\nu-p-1}\to 0$ and $h=O\{n^{-1/(2p+3)\}}$. We assume $p-\nu$ odd and some regularity conditions. Then,

$$n^{(p+1-\nu)/(2p+3)}\left\{ \widehat{g}_\alpha ^{\left( \nu \righ... ...row}\limits_{}^{L}} N\left\{ b_\alpha (x_\alpha),v_\alpha (x_\alpha) \right\},$$

where

$$b_\alpha (x_\alpha)=\frac{\nu ! h_0^{p+1-\nu }}{(p+1)!} \,\mu _{p... ...K_\nu ^{*}\right) \left\{ g_\alpha ^{(p+1)}\left( x_\alpha \right) \right\}\,,$$

and

$$v_\alpha (x_\alpha)=\frac{(\nu !)^2}{h_0^{2\nu +1}}\left\Vert K_\... ...l{x}}_{\underline{\alpha}} \right) } \,d{\boldsymbol{x}}_{\underline{\alpha}}.$$

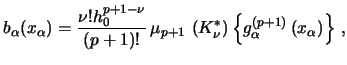
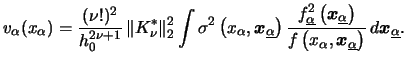
Additionally, for the regression function estimate constructed by the additive component estimates $\widehat{g}_\alpha$ and $\widehat{c}$, i.e.

$$\widehat{m}({\boldsymbol{X}}) = \widehat{c}+\sum^d_{\alpha=1} \widehat{g}_\alpha (X_\alpha)$$

we have:

THEOREM 8.4  
Using the same assumptions as in Theorem 8.3 it holds

$$n^{(p+1)/(2p+3)}\left\{ \widehat{m}\left({\boldsymbol{x}}\right) ... ...w}\limits_{}^{L}} N\left\{ b({\boldsymbol{x}}),v({\boldsymbol{x}})\right\} \,,$$

where ${\boldsymbol{x}}=(x_1,\ldots,x_d)^\top$, $b({\boldsymbol{x}})=\sum_{\alpha =1}^d b_\alpha \left( x_\alpha \right)$ and $v({\boldsymbol{x}})=\sum_{\alpha =1}^dv_\alpha \left( x_\alpha \right) .$

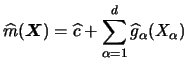
In the following example we illustrate the smoothing properties of this estimator for $\nu = 0$ and $p=1$.

EXAMPLE 8.4  
Consider the same setup as in Example 8.1, but now using $n=150$ observations. In Figure 8.4 we have plotted the true functions (at the corresponding observations $X_{i\alpha}$) and the estimated component functions using marginal integration with the local linear smoothers. The bandwidths are $h=1$ for the first and $h=1.5$ for the other dimensions. Further we set $\widetilde{h}=3$ for all nuisance directions. We used the (product) Quartic kernel for all estimates. As in Example 8.1 the estimated curves reflect almost perfectly the underlying true curves. $\Box$

Figure 8.4: Estimated local linear (solid line) versus true additive component functions (circles at the input values)

8.2.3 Interaction Terms

As pointed out before, marginal integration estimates marginal effects. These are identical to the additive components, if the model is truly additive. But what happens if the underlying model is not purely additive? How do the estimators behave when we have some interaction between explanatory variables, for example given by an additional term $g_{\alpha j}(X_\alpha,X_j)$?

An obvious weakness of the truly additive model is that those interactions are completely ignored, and in certain econometric contexts -- production function modeling being one of them -- the absence of interaction terms has often been criticized. For that reason we will now extend the regression model by pairwise interactions resulting in

$$m({\boldsymbol{x}})=c+\sum_{\alpha = 1}^d g_\alpha (X_\alpha )+\sum_{1\leq \alpha < j \leq d} g_{\alpha j}(X_\alpha ,X_j) \ .$$ (8.20)

Here we use $1\le \alpha <j \le d$ to make sure that we include each pairwise interaction only once. In other words, we assume $g_{\alpha j}= g_{j\alpha}$. Principally, we could also consider interaction terms of higher order than two, but this would make visualization and interpretation hardly possible. Furthermore, the advantage of avoiding the curse of dimensionality would get lost step by step. We will therefore restrict ourselves to the case of only bivariate interactions.

For the marginal integration estimator bivariate interaction terms have been studied in Sperlich et al. (2002). They provide asymptotic properties and additionally introduce test procedures to check for significance of the interactions. In the following we will only sketch the construction of the relevant estimation procedure and its application. For the theoretical results we remark that they are higher dimensional extensions of Theorem 8.3 and refer to the above mentioned article.

For the estimation of (8.20) by marginal integration we have to extend our identification condition

$$E g_\alpha (X_\alpha )=\int g_\alpha (x_\alpha ) f_\alpha (x_\alpha )\,dx_\alpha =0 \quad\textrm{ for all }\alpha,$$ (8.21)

by further ones for the interaction terms:

$$\int g_{\alpha j }(x_\alpha ,x_j ) f_\alpha (x_\alpha )\,dx_\alpha =\int g_{\alpha j }(x_\alpha ,x_ j ) f_ j (x_ j )\,dx_ j =0 \,,$$ (8.22)

with $f_\alpha (\bullet)$, $f_j (\bullet)$ being the marginal densities of the $X_\alpha$ and $X_j$.

As before, equations (8.21) and (8.22) should not be considered as restrictions. It is always possible to shift the functions $g_{\alpha}$ and $g_{\alpha j }$ in the vertical direction without changing the functional forms or the overall regression function. Moreover, all models of the form (8.20) are equivalent to exactly one model satisfying (8.21) and (8.22).

According to the definition of ${\boldsymbol{X}}_{\underline{\alpha}}$, let ${\boldsymbol{X}}_{\underline{\alpha j}}$ now denote the $(d-2)$-dimensional random variable obtained by removing $X_\alpha$ and $X_j$ from ${\boldsymbol{X}}=(X_1,\ldots ,X_d)^\top$. With some abuse of notation we will write ${\boldsymbol{X}}=(X_\alpha ,X_ j ,{\boldsymbol{X}}_{\underline{\alpha j }})$ to highlight the directions in $d$-dimensional space represented by the $\alpha$ and $j$ coordinates. We denote the marginal densities of $X_\alpha$, ${\boldsymbol{X}}_{\underline{\alpha j}}$ and ${\boldsymbol{X}}$ by $f_\alpha (x_\alpha )$, $f_{\underline{\alpha j }}( {\boldsymbol{x}}_{\underline{\alpha j }})$, and $f ({\boldsymbol{x}})$, respectively.

Again consider marginal integration as used before

$$\theta_\alpha (x_\alpha )=\int m(x_\alpha ,{\boldsymbol{x}}\under... ...e{_\alpha })d{\boldsymbol{x}}\underline{_\alpha }\,, \quad 1\leq \alpha \leq d,$$ (8.23)

and in addition

$$\theta_{\alpha j }(x_\alpha ,x_ j )=\int m(x_\alpha ,x_{ j ,}{\bo... ...ldsymbol{x}}\underline{_{\alpha j }})d{\boldsymbol{x}}\underline{_{\alpha j }},$$ (8.24)

$$c_{\alpha j }=\int g_{\alpha j }(x_\alpha,x_j) f_{\alpha j }(x_\alpha,x_j)\,dx_\alpha\,dx_j$$

for every pair $1\leq \alpha < j \leq d$. It can be shown that

$$\theta_{\alpha j }(x_\alpha ,x_ j )-\theta_\alpha (x_\alpha )-\th... ...dsymbol{x}})\,d{\boldsymbol{x}}= g_{\alpha j }(x_\alpha ,x_ j )+c_{\alpha j }.$$

Centering this function in an appropriate way would hence give us the interaction function of interest.

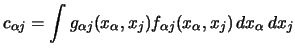
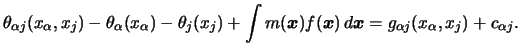
Using the same estimation procedure as described above, i.e., replacing the expectations by averages and the function $m$ by an appropriate pre-estimator, we get estimates for $g_{\alpha}$ and for the interaction terms $g_{\alpha j }$. For the ease of notation we give only the formula for $p=1$, i.e., the local linear estimator, in the pre-estimation step. We obtain

$$\widehat{\{g_{\alpha j}+c_{\alpha j}\}} = \widehat{\theta}_{\alpha j} - \widehat{\theta}_{\alpha} - \widehat{\theta}_{ j} +\widehat{c},$$ (8.25)

where

$$\widehat{\theta}_{\alpha j} = \frac 1n \sum_{j=1}^n {\boldsymbol{... ...)^{-1}{\mathbf{X}}_{\alpha j }^\top {\mathbf{W}}_{l\alpha j }{\boldsymbol{Y}},$$

and

$${\mathbf{W}}_{l\alpha j }=\textrm{diag}\left(\left\{ \frac 1n{\ma... ...}}-{\boldsymbol{x}}_{l\underline{ \alpha j }})\right\} _{i=1,\ldots,n}\right),$$

$${\mathbf{X}}_{\alpha j }=\left( \begin{array}{ccc} 1 & X_{... ... & X_{n\alpha }-x_\alpha & X_{n j }-x_ j \end{array}\right)\,.$$

This is a local linear estimator in the directions $\alpha$, $j$ and a local constant one for the nuisance directions $\underline{\alpha j}$. $\widehat{\theta}_{\alpha}=\widehat{\{g_\alpha +c\}}$, $\widehat{\theta}_{ j}=\widehat{\{g_ j +c\}}$ and $\widehat{c}$ are exactly as defined above.

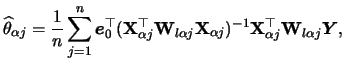
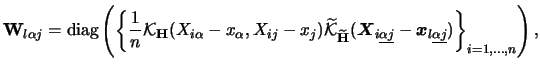
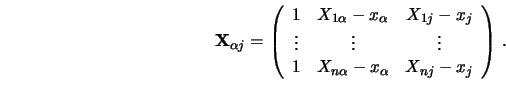
Finally, let us turn to an example, which presents the application of marginal integration estimation, derivative (elasticity) estimation and allows us to illustrate the use of interaction terms.

EXAMPLE 8.5  
Our illustration is based on the example and the data used in Severance-Lossin & Sperlich (1999) who investigated a production function for livestock in Wisconsin. The main interest here is to estimate the impact of various regressors, their return to scale and hence on derivative estimation. Additionally, we validate the additivity assumption by estimating the interaction terms $g_{\alpha j }$.

We use a subset of $n=250$ observations of an original data set of more than 1,000 Wisconsin farms collected by the Farm Credit Service of St. Paul, Minnesota in 1987. Severance-Lossin & Sperlich (1999) removed outliers and incomplete records and selected farms which only produced animal outputs. The data consist of farm level inputs and outputs measured in dollars. In more detail, output $Y$ is livestock, and the input variables are

$X_1$

family labor force,

$X_2$

hired labor force,

$X_3$

miscellaneous inputs (as e.g. repairs, rent, custom hiring, supplies, insurance, gas),

$X_4$

animal inputs (as e.g. purchased feed, breeding, or veterinary services),

$X_5$

intermediate run assets, that is assets with a useful life of one to ten years.

To get an idea of the distribution of the regressors one could plot kernel density estimates for each of them. You would recognize that the regressors are behaving almost normally distributed so that an application of kernel smoother methods should not cause serious numerical problems.

Figure 8.5: Function estimates for the additive components and observations (left), derivative estimates for the parametric (thin lines) and the nonparametric case (right), variables $X_1$ to $X_3$

Figure 8.6: Function estimate for the additive components and observations (left), derivative estimates for the parametric (thin lines) and the nonparametric case (right), variables $X_4$ and $X_5$

A purely additive model (ignoring any possible interaction) is of the form

$$\log \left( Y\right) =c +\sum\limits_{\alpha =1}^d g_\alpha \left\{ \log (X_\alpha) \right\} +\varepsilon\,.$$ (8.26)

This model can be viewed as a generalization of the Cobb-Douglas production, where $g_\alpha \left\{ \log (X_\alpha) \right\} = \beta_\alpha \log (X_\alpha )$ (see (5.4)). Additionally, we allow for inclusion of interaction terms $g_{\alpha j }$ and obtain

$$\log \left( Y\right) =c + \sum\limits_{\alpha =1}^d g_\alpha \lef... ...e d} g_{\alpha j} \left\{ \log (X_\alpha) ,\log (X_ j) \right\} +\varepsilon\,.$$ (8.27)

The important point to understand in marginal integration is that the estimation of the one-dimensional component functions is not affected by the inclusion of interaction terms. This means, whether we estimate in model (8.26) or in (8.27) does not change the results for the estimation of the marginal functions $g_\alpha$.

The results are given in Figures 8.5, 8.6. We use (product) Quartic kernels for all dimensions and bandwidths proportional to the standard deviation of $X_\alpha$ ( $h_\alpha=1.5\,\sigma_\alpha$, $\widetilde{h}_\alpha=4\,h_\alpha$). It is known that the integration estimator is quite robust against different choices of bandwidths, see e.g. Sperlich et al. (1999).

To highlight the shape of the estimates we display the main part of the point clouds including the function estimates. The graphs give some indication of nonlinearity, in particular for $X_1$, $X_2$ and $X_5$. The derivatives seem to indicate that the elasticities for these inputs increase and could finally lead to increasing returns to scale. Note that for all dimensions (especially where the mass of the observations is located) the nonparametric results differ a lot from the parametric case. An obvious conclusion from the economic point of view is that for instance larger farms are more productive (intuitively quite reasonable).

Figure 8.7: Estimates for interaction terms for Wisconsin farm data

Figure 8.8: Estimates for interaction terms for Wisconsin farm data

In Figures 8.7 to 8.8 we present the estimates of the bivariate interaction terms $g_{\alpha j }$. For their estimation and graphical presentation we trimmed the data by removing $2\%$ of the most extreme observations. Again Quartic kernels were used, here with bandwidths $h_\alpha = 1.7 \,\sigma_\alpha$ and $\widetilde{h}_\alpha$ as above.

Obviously, often it is hard to interpret those interaction terms. But as long as we can visualize relationships a careful interpretation can be tried. Sperlich et al. (2002) find that a weak form of interaction is present. The variable $X_1$ (family labor) plays an important role in the interactions, especially $g_{1,3}$ (family labor and miscellaneous inputs), $g_{1,5}$ (family labor and intermediate run assets) and $g_{3,5}$ (miscellaneous inputs and intermediate run assets) should be taken into account. $\Box$