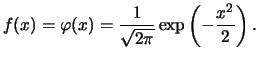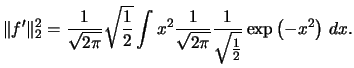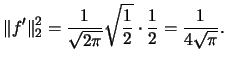Let us investigate some of the properties of the histogram as an
estimator of the unknown pdf 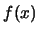 .
Suppose that the origin
.
Suppose that the origin 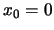 and that we want to estimate
the density at some point
and that we want to estimate
the density at some point
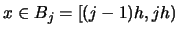 . The density
estimate assigned by the histogram to
. The density
estimate assigned by the histogram to 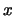 is
is
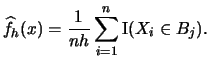 |
(2.6) |
Is
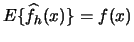 , i.e. is the histogram an
unbiased estimator? Let us calculate
, i.e. is the histogram an
unbiased estimator? Let us calculate
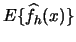 to
find out:
to
find out:
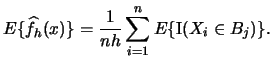 |
(2.7) |
Since the
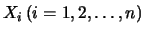 are i.i.d. random variables
it follows that the indicator functions
are i.i.d. random variables
it follows that the indicator functions
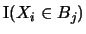 are also i.i.d. random variables,
and we can write
are also i.i.d. random variables,
and we can write
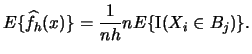 |
(2.8) |
It remains to find
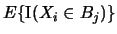 . It is
straightforward to
derive the pdf of the random variable
. It is
straightforward to
derive the pdf of the random variable
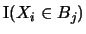 :
:
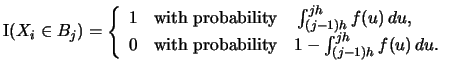 |
(2.9) |
Hence it is Bernoulli distributed and
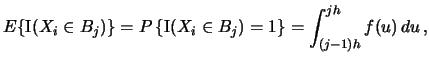 |
(2.10) |
therefore
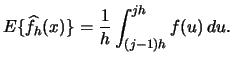 |
(2.11) |
The last term is in general not equal to 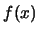 . Consequently,
the histogram is in general not an unbiased estimator of
. Consequently,
the histogram is in general not an unbiased estimator of 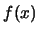 :
:
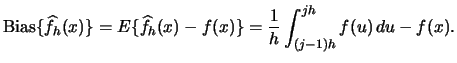 |
(2.12) |
The precise value of the bias depends on the shape of the true
density 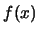 . We can, however, derive an approximative bias formula
that allows us to make some general remarks about the
situations that lead to a small or large bias.
Using
. We can, however, derive an approximative bias formula
that allows us to make some general remarks about the
situations that lead to a small or large bias.
Using
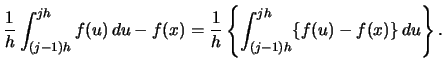 |
(2.13) |
and a first-order Taylor approximation
of 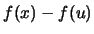 around the center
around the center
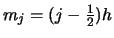 of
of 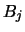 , i.e.
, i.e.
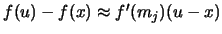 yields
yields
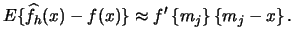 |
(2.14) |
Note that the absolute value of the approximate bias is increasing in the slope of the true density at the mid point 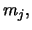 and that the approximate bias is zero if
and that the approximate bias is zero if 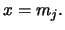
Let us calculate the variance of the histogram to see how its
volatility depends on the binwidth 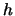 :
:
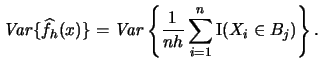 |
(2.15) |
Since the 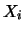 are i.i.d. we can write
are i.i.d. we can write
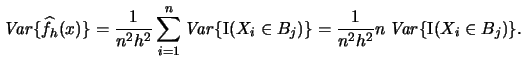 |
(2.16) |
From (2.9) we know
that
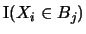 is
Bernoulli distributed with parameter
is
Bernoulli distributed with parameter
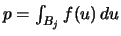 . Since
the variance of any Bernoulli random variable
. Since
the variance of any Bernoulli random variable 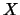 is given by
is given by
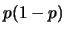 we have
we have
You are asked in Exercise 2.3 to show that the right hand side of (2.17) can be written as the sum of 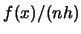 and terms that are of smaller magnitude. That is, you are asked to show that there also exists an approximate formula for the variance of
and terms that are of smaller magnitude. That is, you are asked to show that there also exists an approximate formula for the variance of
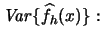
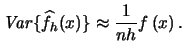 |
(2.17) |
We observe that the variance of the histogram is proportional to
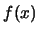 and decreases when
and decreases when 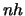 increases. This implies that increasing
increases. This implies that increasing
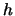 will reduce the variance.
We know from (2.14)
that increasing
will reduce the variance.
We know from (2.14)
that increasing 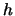 will do the opposite to the bias.
So how should we choose
will do the opposite to the bias.
So how should we choose 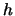 if we want to have a small
variance and a small bias?
if we want to have a small
variance and a small bias?
Since variance and bias vary in opposite directions with 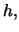 we have to
settle for finding the value of
we have to
settle for finding the value of 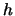 that yields (in some sense)
the optimal compromise between variance and bias reduction.
that yields (in some sense)
the optimal compromise between variance and bias reduction.
Consider the mean squared error (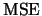 ) of the histogram
) of the histogram
![$\displaystyle \mse\{\widehat f_{h}(x)\}=E[\{\widehat f_{h}(x)-f(x)\}^{2}],$](spmhtmlimg468.gif) |
(2.18) |
which can be written as the sum of the variance and the squared
bias (this is a general result,
not limited to this particular problem)
![$\displaystyle \mse\{\widehat f_{h}(x)\} =\mathop{\mathit{Var}}\{\widehat f_{h}(x)\}+[\bias\{\widehat{f}_{h}(x)\}]^{2}.$](spmhtmlimg469.gif) |
(2.19) |
Hence, finding the binwidth 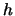 that minimizes the
that minimizes the 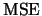 might
yield a histogram that is neither oversmoothed (i.e. one that
overemphasizes variance reduction by employing a relatively large
value of
might
yield a histogram that is neither oversmoothed (i.e. one that
overemphasizes variance reduction by employing a relatively large
value of 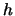 ) nor undersmoothed (i.e. one that is overemphasizes
bias reduction by using a small binwidth).
It can be shown (see Exercise 2.4) that
) nor undersmoothed (i.e. one that is overemphasizes
bias reduction by using a small binwidth).
It can be shown (see Exercise 2.4) that
where 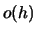 and
and
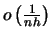 denote
terms not explicitly written down which are of lower
order than
denote
terms not explicitly written down which are of lower
order than 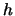 and
and
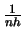 , respectively.
, respectively.
From (2.21) we can conclude that the histogram converges in mean
square to
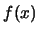 if we let
if we let 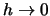 ,
,
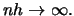 That is, if we use more and
more observations (
That is, if we use more and
more observations (
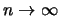 ) and smaller and smaller binwidth (
) and smaller and smaller binwidth (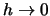 )
but do not shrink the binwidth too quickly (
)
but do not shrink the binwidth too quickly (
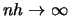 ) then the
) then the 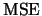 of
of
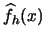 goes to zero. Since convergence in mean square
implies convergence in probability, it follows that
goes to zero. Since convergence in mean square
implies convergence in probability, it follows that
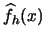 converges to
converges to 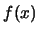 in probability or, in other words, that
in probability or, in other words, that
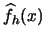 is a consistent estimator of
is a consistent estimator of 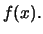
Figure 2.4 shows the 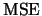 (at
(at 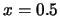 ) for estimating
the density function given in Exercise 2.9 as a function of
the binwidth
) for estimating
the density function given in Exercise 2.9 as a function of
the binwidth 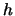 .
.
Figure:
Squared bias
(thin solid line), variance (dashed line)
and 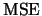 (thick line) for the histogram
(thick line) for the histogram
![\includegraphics[width=0.03\defepswidth]{quantlet.ps}](spmhtmlimg1.gif) SPMhistmse
SPMhistmse
|
|
The application of the 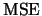 formula is difficult in practice,
since the derived formula for the
formula is difficult in practice,
since the derived formula for the 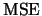 depends on
the unknown
density function
depends on
the unknown
density function 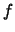 both in the variance and the squared bias term.
Instead of looking at the accuracy of
both in the variance and the squared bias term.
Instead of looking at the accuracy of
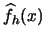 as an
estimator of
as an
estimator of 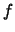 at a single point, it might be
worthwhile to have a global measure of accuracy. The most widely
used global measure of estimation accuracy is the mean integrated
squared error (
at a single point, it might be
worthwhile to have a global measure of accuracy. The most widely
used global measure of estimation accuracy is the mean integrated
squared error (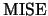 ):
):
Using (2.21) we can write for any 
Here,
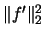 denotes the so-called
squared
denotes the so-called
squared 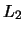 -norm of the function
-norm of the function 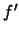 .
Now, the asymptotic
.
Now, the asymptotic 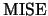 ,
denoted
,
denoted 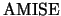 , is given by
, is given by
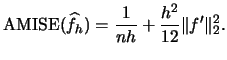 |
(2.23) |
We are now in a position to employ a precise criterion for
selecting an optimal binwidth
 : select the binwidth
: select the binwidth  that minimizes
that minimizes
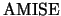 !
Differentiating
!
Differentiating 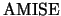 with respect to
with respect to 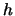 gives
gives
hence
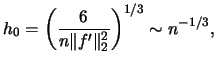 |
(2.24) |
where 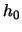 denotes the optimal binwidth.
Looking at (2.25) it becomes clear that we run into a
problem if
we want to calculate
denotes the optimal binwidth.
Looking at (2.25) it becomes clear that we run into a
problem if
we want to calculate 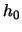 since
since
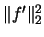 is unknown.
is unknown.
A way out of this dilemma will be described later, when we deal
with kernel density estimation. For the moment, assume that we
know the true density 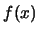 . More specifically assume a standard
normal distribution, i.e.
. More specifically assume a standard
normal distribution, i.e.
In order to calculate 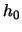 we have to find
we have to find
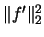 . Using the fact that for the standard normal distribution
. Using the fact that for the standard normal distribution
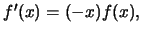 it can be shown that
Since the term inside the integral is just the formula for
computing the variance of a random variable that follows a normal
distribution with mean
it can be shown that
Since the term inside the integral is just the formula for
computing the variance of a random variable that follows a normal
distribution with mean 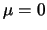 and variance
and variance
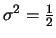 ,
we can write
,
we can write
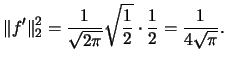 |
(2.25) |
Using this result we can calculate 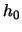 for this application:
for this application:
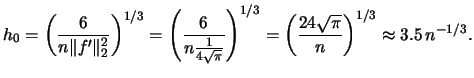 |
(2.26) |
Unfortunately, in practice we do not know 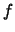 (if we
did there would be no point in estimating it). However,
(2.27) can serve as a rule-of-thumb binwidth
(Scott, 1992, Subsection 3.2.3).
(if we
did there would be no point in estimating it). However,
(2.27) can serve as a rule-of-thumb binwidth
(Scott, 1992, Subsection 3.2.3).
![]() .
Suppose that the origin
.
Suppose that the origin ![]() and that we want to estimate
the density at some point
and that we want to estimate
the density at some point
![]() . The density
estimate assigned by the histogram to
. The density
estimate assigned by the histogram to ![]() is
is
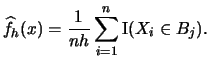
![]() , i.e. is the histogram an
unbiased estimator? Let us calculate
, i.e. is the histogram an
unbiased estimator? Let us calculate
![]() to
find out:
to
find out:
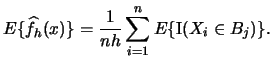
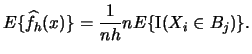
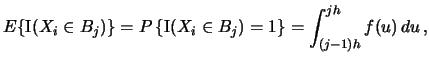
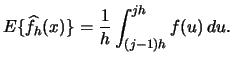
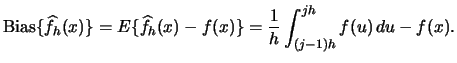
![]() :
:
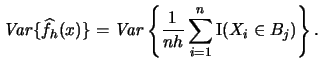
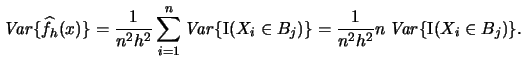
![]() and terms that are of smaller magnitude. That is, you are asked to show that there also exists an approximate formula for the variance of
and terms that are of smaller magnitude. That is, you are asked to show that there also exists an approximate formula for the variance of
![]()
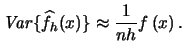
![]() we have to
settle for finding the value of
we have to
settle for finding the value of ![]() that yields (in some sense)
the optimal compromise between variance and bias reduction.
that yields (in some sense)
the optimal compromise between variance and bias reduction.
![]() ) of the histogram
) of the histogram
![]() if we let
if we let ![]() ,
,
![]() That is, if we use more and
more observations (
That is, if we use more and
more observations (
![]() ) and smaller and smaller binwidth (
) and smaller and smaller binwidth (![]() )
but do not shrink the binwidth too quickly (
)
but do not shrink the binwidth too quickly (
![]() ) then the
) then the ![]() of
of
![]() goes to zero. Since convergence in mean square
implies convergence in probability, it follows that
goes to zero. Since convergence in mean square
implies convergence in probability, it follows that
![]() converges to
converges to ![]() in probability or, in other words, that
in probability or, in other words, that
![]() is a consistent estimator of
is a consistent estimator of ![]()
![]() (at
(at ![]() ) for estimating
the density function given in Exercise 2.9 as a function of
the binwidth
) for estimating
the density function given in Exercise 2.9 as a function of
the binwidth ![]() .
.
![\includegraphics[width=1.2\defpicwidth]{SPMhistmse.ps}](spmhtmlimg482.gif)
![]() formula is difficult in practice,
since the derived formula for the
formula is difficult in practice,
since the derived formula for the ![]() depends on
the unknown
density function
depends on
the unknown
density function ![]() both in the variance and the squared bias term.
Instead of looking at the accuracy of
both in the variance and the squared bias term.
Instead of looking at the accuracy of
![]() as an
estimator of
as an
estimator of ![]() at a single point, it might be
worthwhile to have a global measure of accuracy. The most widely
used global measure of estimation accuracy is the mean integrated
squared error (
at a single point, it might be
worthwhile to have a global measure of accuracy. The most widely
used global measure of estimation accuracy is the mean integrated
squared error (![]() ):
):
![$\displaystyle E\left[\int^{\infty}_{-\infty} \{\widehat
f_{h}(x)-f(x)\}^{2}\,dx\right]$](spmhtmlimg485.gif)
![$\displaystyle \int^{\infty}_{-\infty}E\left[\{\widehat
f_{h}(x)-f(x)\}^{2}\right]\,dx$](spmhtmlimg486.gif)
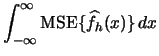
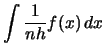
![$\displaystyle +\int \sum_{j}\Ind(x\in B_{j})
\left\{\left(j-\frac{1}{2}\right)h-x\right\}^{2} \left[f'\left\{\left(j-\frac{1}{2}\right)h\right\}
\right]^{2}\,dx$](spmhtmlimg490.gif)
![$\displaystyle \frac{1}{nh}+\sum_{j}\int_{B_{j}}
\left\{x-\left(j-\frac{1}{2}\ri...
...\right\}^{2}
\left\{f'\left[\left(j-\frac{1}{2}\right)h\right] \right\}^{2}\,dx$](spmhtmlimg491.gif)
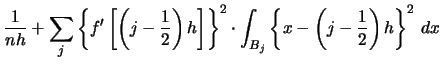
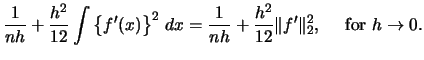
![]() : select the binwidth
: select the binwidth ![]() that minimizes
that minimizes
![]() !
Differentiating
!
Differentiating ![]() with respect to
with respect to ![]() gives
gives
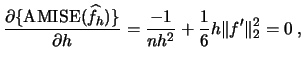
![]() . More specifically assume a standard
normal distribution, i.e.
. More specifically assume a standard
normal distribution, i.e.