2.2 Spectral Decompositions
The computation of eigenvalues and eigenvectors is an important issue in
the analysis of matrices.
The spectral decomposition or Jordan decomposition links the structure of
a matrix to the eigenvalues and the eigenvectors.
THEOREM 2.1 (Jordan Decomposition)
Each symmetric matrix
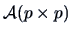
can be written as
 |
(2.18) |
where
and where
is an orthogonal matrix consisting of the eigenvectors
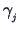
of
.
EXAMPLE 2.4
Suppose that
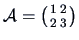
.
The eigenvalues are found by solving
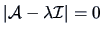
.
This is equivalent to
Hence, the eigenvalues are
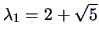
and
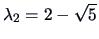
.
The eigenvectors are
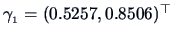
and
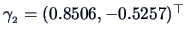
.
They are orthogonal since
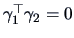
.
Using spectral decomposition, we can define powers of a matrix
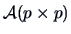 . Suppose
. Suppose 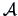 is a symmetric matrix.
Then by Theorem 2.1
is a symmetric matrix.
Then by Theorem 2.1
and we define for some
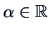
 |
(2.19) |
where
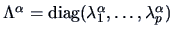 .
In particular, we can easily calculate the inverse of the matrix
.
In particular, we can easily calculate the inverse of the matrix
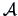 . Suppose that the eigenvalues of
. Suppose that the eigenvalues of 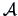 are positive. Then
with
are positive. Then
with 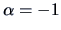 , we obtain the inverse of
, we obtain the inverse of 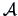 from
from
 |
(2.20) |
Another interesting decomposition which is later used is given in
the following theorem.
THEOREM 2.2 (Singular Value Decomposition
)
Each matrix
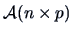
with rank
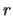
can be decomposed as
where
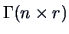
and
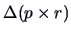
. Both
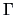
and

are column orthonormal, i.e.,
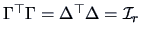
and
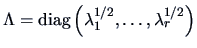
,
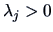
.
The values
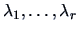
are the non-zero eigenvalues of the
matrices
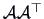
and
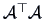
.
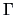
and

consist of the corresponding
eigenvectors of
these matrices.
This is obviously a generalization of Theorem 2.1 (Jordan
decomposition). With Theorem 2.2, we can find a 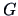 -inverse
-inverse
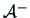 of
of 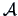 . Indeed, define
. Indeed, define
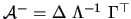 . Then
. Then
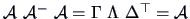 . Note that the
. Note that the 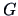 -inverse is
not unique.
-inverse is
not unique.
EXAMPLE 2.5
In Example
2.2, we showed that the generalized inverse
of
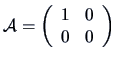
is
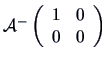
. The following also holds
which means that the matrix
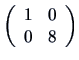
is also a generalized inverse of
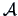
.
Summary

- The Jordan decomposition gives a representation of a
symmetric matrix in terms of eigenvalues and eigenvectors.

- The eigenvectors belonging to the largest eigenvalues
indicate the ``main direction'' of the data.

- The Jordan decomposition allows one to easily compute the power
of a symmetric matrix
 :
:
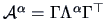 .
.

- The singular value decomposition (SVD) is a generalization
of the Jordan decomposition to non-quadratic matrices.
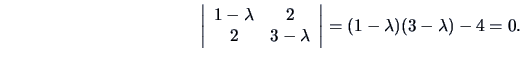
![]() . Suppose
. Suppose ![]() is a symmetric matrix.
Then by Theorem 2.1
is a symmetric matrix.
Then by Theorem 2.1
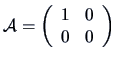 is
is
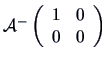 . The following also holds
. The following also holds
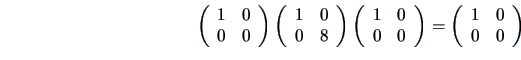
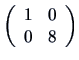 is also a generalized inverse of
is also a generalized inverse of