2.3 Quadratic Forms
A quadratic form 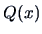 is built from a symmetric matrix
is built from a symmetric matrix
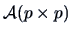 and a vector
and a vector
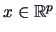 :
:
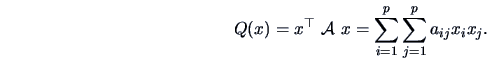 |
(2.21) |
Definiteness of Quadratic Forms and Matrices
A matrix 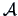 is called positive definite (semidefinite)
if the corresponding quadratic form
is called positive definite (semidefinite)
if the corresponding quadratic form 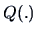 is positive definite
(semidefinite). We write
is positive definite
(semidefinite). We write
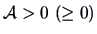 .
.
Quadratic forms can always be diagonalized, as the following result shows.
THEOREM 2.3
If
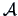
is symmetric and
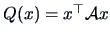
is the corresponding quadratic form,
then there exists a transformation
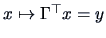
such that
where
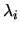
are the eigenvalues of
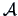
.
PROOF:
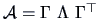 .
By Theorem 2.1 and
.
By Theorem 2.1 and
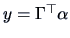 we have that
we have that
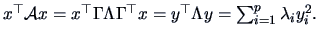

Positive definiteness of quadratic forms can be deduced from positive
eigenvalues.
PROOF:
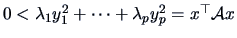 for all
for all 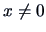 by Theorem 2.3.
by Theorem 2.3.

COROLLARY 2.1
If
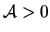
, then
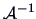
exists and
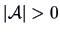
.
EXAMPLE 2.6
The quadratic form
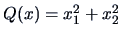
corresponds to the matrix
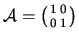
with eigenvalues
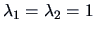
and is thus positive definite.
The quadratic form
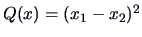
corresponds to the matrix
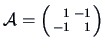
with eigenvalues
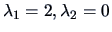
and is
positive semidefinite.
The quadratic form
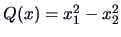
with eigenvalues
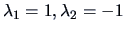
is indefinite.
In the statistical analysis of multivariate data, we are interested in
maximizing quadratic forms given some constraints.
THEOREM 2.5
If
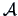
and
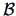
are symmetric and
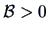
,
then the maximum of
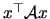
under
the constraints
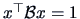
is given by the largest eigenvalue
of
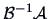
. More generally,
where
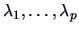
denote the eigenvalues of
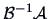
. The vector which maximizes (minimizes)
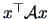
under the constraint
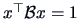
is the eigenvector of
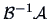
which corresponds to the
largest (smallest) eigenvalue of
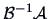
.
PROOF:
By definition,
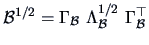 .
Set
.
Set
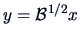 , then
, then
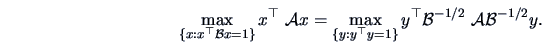 |
(2.22) |
From Theorem 2.1, let
be the spectral decomposition of
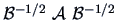 . Set
. Set
Thus (2.22) is equivalent to
But
The maximum is thus obtained by
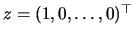 , i.e.,
, i.e.,
Since
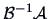 and
and
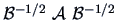 have the same eigenvalues, the
proof is complete.
have the same eigenvalues, the
proof is complete.

EXAMPLE 2.7
Consider the following matrices
We calculate
The biggest eigenvalue of the matrix
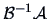
is
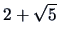
.
This means that the maximum of
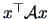
under the constraint
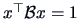
is
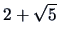
.
Notice that the constraint
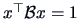 corresponds, with our choice of
corresponds, with our choice of
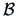 , to the points which lie on the unit circle
, to the points which lie on the unit circle 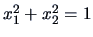 .
.
Summary

- A quadratic form can be described by a symmetric matrix
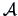 .
.

- Quadratic forms can always be diagonalized.

- Positive definiteness of a quadratic form is equivalent to positiveness
of the eigenvalues of the matrix
 .
.

- The maximum and minimum of a quadratic form given some constraints can be
expressed in terms of eigenvalues.
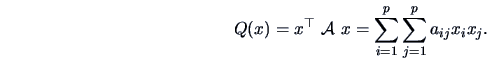
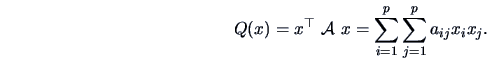
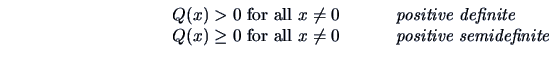

![]() .
By Theorem 2.1 and
.
By Theorem 2.1 and
![]() we have that
we have that
![]()
![]()
![]() for all
for all ![]() by Theorem 2.3.
by Theorem 2.3.
![]()
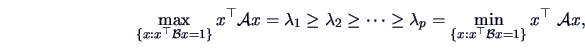
![]() .
Set
.
Set
![]() , then
, then
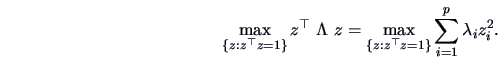
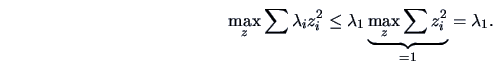
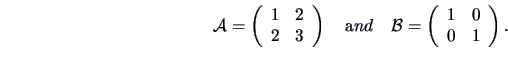

![]() corresponds, with our choice of
corresponds, with our choice of
![]() , to the points which lie on the unit circle
, to the points which lie on the unit circle ![]() .
.