3.5 Simple Analysis of Variance
In a simple (i.e., one-factorial) analysis of variance
(ANOVA), it is
assumed that the average values of the response variable 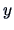 are induced by one simple factor. Suppose that this factor
takes on
are induced by one simple factor. Suppose that this factor
takes on  values and that for each factor level, we have
values and that for each factor level, we have
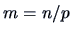 observations. The sample is of the
form given in Table 3.1, where all of
the observations are independent.
observations. The sample is of the
form given in Table 3.1, where all of
the observations are independent.
Table 3.1:
Observation
structure of a simple ANOVA.
| sample element |
factor levels 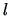 |
| 1 |
 |
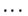 |
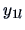 |
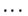 |
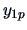 |
| 2 |
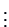 |
|
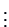 |
|
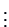 |
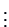 |
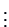 |
|
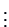 |
|
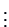 |
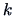 |
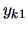 |
 |
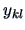 |
 |
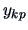 |
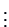 |
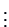 |
|
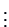 |
|
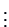 |
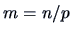 |
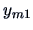 |
 |
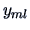 |
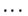 |
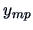 |
|
The goal of a simple ANOVA is to analyze the observation structure
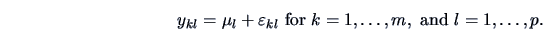 |
(3.41) |
Each factor has a mean value 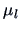 . Each observation
. Each observation 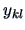 is assumed to be a sum of the corresponding factor mean value
is assumed to be a sum of the corresponding factor mean value
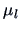 and a zero mean random error
and a zero mean random error
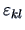 .
The linear regression model falls into this scheme with
.
The linear regression model falls into this scheme with 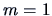 ,
, 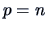 and
and
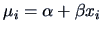 , where
, where 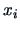 is the
is the 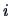 -th level
value of the factor.
-th level
value of the factor.
EXAMPLE 3.14
The ``classic blue'' pullover company analyzes the effect of three
marketing strategies
| 1 |
advertisement in local newspaper, |
| 2 |
presence of sales assistant, |
| 3 |
luxury presentation in shop windows. |
All of these strategies are tried in 10 different shops.
The resulting sale observations are given in Table 3.2.
Table 3.2:
Pullover
sales as function of marketing strategy.
| shop |
marketing strategy |
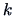 |
factor l |
| |
1 |
|
2 |
|
3 |
| 1 |
9 |
|
10 |
|
18 |
| 2 |
11 |
|
15 |
|
14 |
| 3 |
10 |
|
11 |
|
17 |
| 4 |
12 |
|
15 |
|
9 |
| 5 |
7 |
|
15 |
|
14 |
| 6 |
11 |
|
13 |
|
17 |
| 7 |
12 |
|
7 |
|
16 |
| 8 |
10 |
|
15 |
|
14 |
| 9 |
11 |
|
13 |
|
17 |
| 10 |
13 |
|
10 |
|
15 |
|
There are 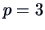 factors and
factors and 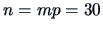 observations in the data.
The ``classic blue'' pullover company wants to know whether all three
marketing strategies have the same mean effect or whether there are
differences. Having the same effect means that all
observations in the data.
The ``classic blue'' pullover company wants to know whether all three
marketing strategies have the same mean effect or whether there are
differences. Having the same effect means that all 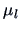 in
(3.41)
equal one value,
in
(3.41)
equal one value, 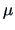 . The hypothesis to be tested is therefore
. The hypothesis to be tested is therefore
The alternative hypothesis, that the
marketing strategies have different effects, can be formulated as
This means that one marketing strategy is better than the others.
The method used to test this problem is to compute as in
(3.38) the
total variation and to decompose it into the sources of variation.
This gives:
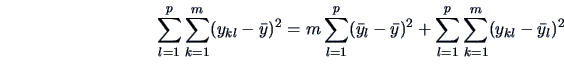 |
(3.42) |
The total variation (sum of squares=SS) is:
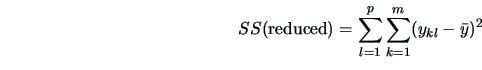 |
(3.43) |
where
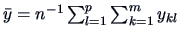 is the
overall mean.
Here the total variation is denoted as
is the
overall mean.
Here the total variation is denoted as
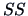 ( reduced), since in comparison
with the model under the alternative
( reduced), since in comparison
with the model under the alternative 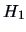 ,
we have a reduced set of parameters. In fact there is
1 parameter
,
we have a reduced set of parameters. In fact there is
1 parameter 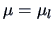 under
under 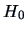 . Under
. Under 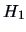 , the ``full'' model, we
have three parameters, namely the three different means
, the ``full'' model, we
have three parameters, namely the three different means 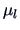 .
.
The variation under
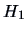 is therefore:
is therefore:
 |
(3.44) |
where
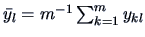 is the mean of each
factor
is the mean of each
factor 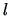 . The hypothetical model
. The hypothetical model 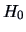 is called reduced, since it has
(relative to
is called reduced, since it has
(relative to 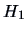 ) fewer parameters.
) fewer parameters.
The 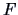 -test of the linear hypothesis is used to compare the
difference in the variations under the reduced model
-test of the linear hypothesis is used to compare the
difference in the variations under the reduced model 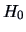 (3.43) and
the full model
(3.43) and
the full model 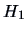 (3.44) to the variation under the full model
(3.44) to the variation under the full model
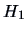 :
:
 |
(3.45) |
Here 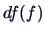 and
and 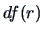 denote the
degrees of freedom
under the full model and the reduced model respectively.
The degrees of freedom are essential in specifying the shape
of the
denote the
degrees of freedom
under the full model and the reduced model respectively.
The degrees of freedom are essential in specifying the shape
of the 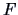 -distribution. They have a simple interpretation:
-distribution. They have a simple interpretation:
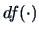 is equal to the
number of observations minus the number of parameters in the model.
is equal to the
number of observations minus the number of parameters in the model.
From Example 3.14, 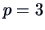 parameters are estimated under the full
model, i.e.,
parameters are estimated under the full
model, i.e.,
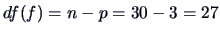 . Under the reduced model, there is one parameter to estimate,
namely the overall mean, i.e.,
. Under the reduced model, there is one parameter to estimate,
namely the overall mean, i.e., 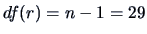 . We can compute
. We can compute
and
The 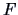 -statistic (3.45) is therefore
-statistic (3.45) is therefore
This value needs to be compared to the quantiles of the 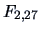 distribution.
Looking up the critical values in a
distribution.
Looking up the critical values in a 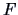 -distribution shows that the test
statistic above is highly significant.
We conclude that the marketing strategies
have different effects.
-distribution shows that the test
statistic above is highly significant.
We conclude that the marketing strategies
have different effects.
The 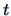 -test of a linear regression model can be put into this
framework. For a linear regression model (3.27),
the reduced model is the one with
-test of a linear regression model can be put into this
framework. For a linear regression model (3.27),
the reduced model is the one with 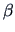 = 0:
= 0:
The reduced model has 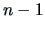 degrees of freedom and one parameter,
the intercept
degrees of freedom and one parameter,
the intercept 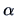 .
.
The full model is given by 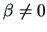 ,
,
and has 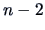 degrees of freedom, since there are
two parameters
degrees of freedom, since there are
two parameters
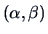 .
.
The 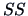 ( reduced) equals
( reduced) equals
The 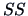 ( full) equals
( full) equals
The 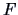 -test is therefore, from (3.45),
-test is therefore, from (3.45),
Using the estimators 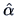 and
and
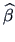 the explained variation is:
the explained variation is:
From (3.32) the 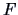 -ratio (3.46) is therefore:
-ratio (3.46) is therefore:
The 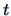 -test statistic (3.33)
is just the square root of the
-test statistic (3.33)
is just the square root of the 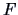 - statistic (3.49).
- statistic (3.49).
Note, using (3.39) the 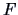 -statistic can be rewritten as
-statistic can be rewritten as
In the pullover Example 3.11, we obtain
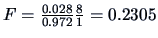 ,
so that the null hypothesis
,
so that the null hypothesis 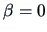 cannot be rejected. We conclude
therefore that there is only a minor influence of prices on sales.
cannot be rejected. We conclude
therefore that there is only a minor influence of prices on sales.
Summary

- Simple ANOVA models an output
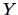 as a function of
one factor.
as a function of
one factor.

- The reduced model is the hypothesis of equal
means.

- The full model is the alternative hypothesis of
different means.

- The
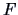 -test is based on a comparison of the sum of
squares under the full and the reduced models.
-test is based on a comparison of the sum of
squares under the full and the reduced models.

- The degrees of freedom are calculated as the number of
observations minus the number of parameters.

- The
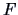 -statistic is
-statistic is

- The
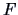 -test rejects the null hypothesis
if the
-test rejects the null hypothesis
if the 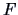 -statistic is larger than the 95%
quantile of the
-statistic is larger than the 95%
quantile of the
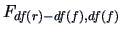 distribution.
distribution.

- The
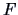 -test statistic for the slope of the linear regression
model
-test statistic for the slope of the linear regression
model
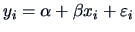 is the square of the
is the square of the
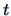 -test statistic.
-test statistic.
![]() factors and
factors and ![]() observations in the data.
The ``classic blue'' pullover company wants to know whether all three
marketing strategies have the same mean effect or whether there are
differences. Having the same effect means that all
observations in the data.
The ``classic blue'' pullover company wants to know whether all three
marketing strategies have the same mean effect or whether there are
differences. Having the same effect means that all ![]() in
(3.41)
equal one value,
in
(3.41)
equal one value, ![]() . The hypothesis to be tested is therefore
. The hypothesis to be tested is therefore
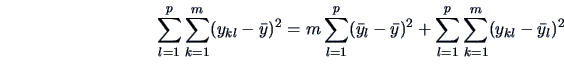
![]() is therefore:
is therefore:
![]() -test of the linear hypothesis is used to compare the
difference in the variations under the reduced model
-test of the linear hypothesis is used to compare the
difference in the variations under the reduced model ![]() (3.43) and
the full model
(3.43) and
the full model ![]() (3.44) to the variation under the full model
(3.44) to the variation under the full model
![]() :
:
![]() and
and ![]() denote the
degrees of freedom
under the full model and the reduced model respectively.
The degrees of freedom are essential in specifying the shape
of the
denote the
degrees of freedom
under the full model and the reduced model respectively.
The degrees of freedom are essential in specifying the shape
of the ![]() -distribution. They have a simple interpretation:
-distribution. They have a simple interpretation:
![]() is equal to the
number of observations minus the number of parameters in the model.
is equal to the
number of observations minus the number of parameters in the model.
![]() parameters are estimated under the full
model, i.e.,
parameters are estimated under the full
model, i.e.,
![]() . Under the reduced model, there is one parameter to estimate,
namely the overall mean, i.e.,
. Under the reduced model, there is one parameter to estimate,
namely the overall mean, i.e., ![]() . We can compute
. We can compute
![]() -statistic (3.45) is therefore
-statistic (3.45) is therefore
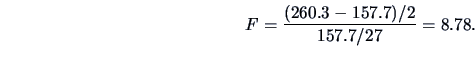
![]() -test of a linear regression model can be put into this
framework. For a linear regression model (3.27),
the reduced model is the one with
-test of a linear regression model can be put into this
framework. For a linear regression model (3.27),
the reduced model is the one with ![]() = 0:
= 0:
![]() ,
,
![]() ( reduced) equals
( reduced) equals
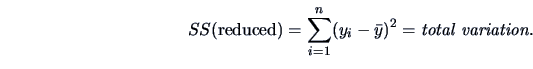
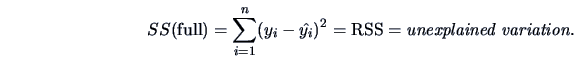
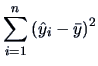
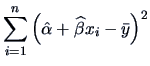
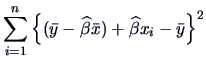
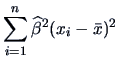
![]() -statistic can be rewritten as
-statistic can be rewritten as

