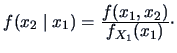4.1 Distribution and Density Function
Let
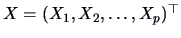 be a random vector.
The cumulative distribution function (cdf) of
be a random vector.
The cumulative distribution function (cdf) of  is defined by
is defined by
For continuous  ,
there exists a nonnegative probability density function (pdf)
,
there exists a nonnegative probability density function (pdf) 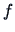 , such that
, such that
 |
(4.1) |
Note that
Most of the
integrals appearing below are multidimensional. For instance,
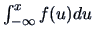 means
means
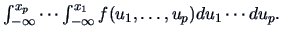 Note also that the cdf
Note also that the cdf 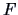 is differentiable with
is differentiable with
For discrete  , the values of this random variable are concentrated on a
countable or finite set of points
, the values of this random variable are concentrated on a
countable or finite set of points
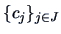 , the
probability of events of the form
, the
probability of events of the form 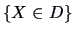 can then be computed as
can then be computed as
If we partition  as
as
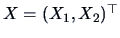 with
with
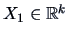 and
and
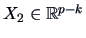 , then the function
, then the function
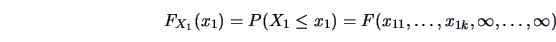 |
(4.2) |
is called the marginal cdf. 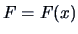 is called the joint cdf.
For continuous
is called the joint cdf.
For continuous  the marginal pdf can be computed from the joint density
by ``integrating out'' the variable not of interest.
the marginal pdf can be computed from the joint density
by ``integrating out'' the variable not of interest.
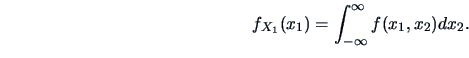 |
(4.3) |
The conditional pdf of 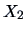 given
given 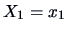 is given as
is given as
 |
(4.4) |
EXAMPLE 4.1
Consider the pdf
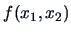
is a density since
The marginal densities
are
The conditional densities
are therefore
Note that these conditional pdf's are nonlinear in
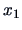
and
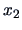
although the joint pdf has a simple (linear) structure.
Independence of two random variables is defined as follows.
DEFINITION 4.1
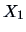
and
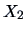
are independent
iff
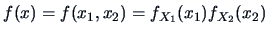
.
That is, 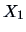 and
and 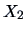 are independent if
the conditional pdf's are equal to the marginal
densities, i.e.,
are independent if
the conditional pdf's are equal to the marginal
densities, i.e.,
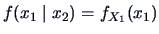 and
and
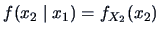 . Independence can be interpreted
as follows: knowing
. Independence can be interpreted
as follows: knowing 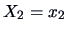 does not change the probability assessments
on
does not change the probability assessments
on 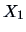 , and conversely.
, and conversely.
1mm
![\begin{picture}(2.00,2.00)
\par\linethickness{1.0pt}\put(0.00,0.00){\line(1,0){1...
...\line(1,-2){5.00}}
\put(5.00,4.00){\makebox(0,0)[cc]{\LARGE\bf !}}
\end{picture}](mvahtmlimg711.gif)
Different joint pdf's
may have the same marginal pdf's.
EXAMPLE 4.2
Consider the pdf's
and
We compute in both cases the marginal pdf's as
Indeed
Hence we obtain identical marginals from
different joint distributions!
Let us study the concept of independence using the bank notes example.
Consider the variables 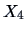 (lower inner frame) and
(lower inner frame) and 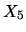 (upper
inner frame).
From Chapter 3, we already know that they
have significant correlation, so they are almost surely not independent.
Kernel estimates of the marginal densities,
(upper
inner frame).
From Chapter 3, we already know that they
have significant correlation, so they are almost surely not independent.
Kernel estimates of the marginal densities,
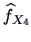 and
and
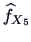 , are given in Figure 4.1.
In Figure 4.2 (left) we show the product of these two
densities.
The kernel density technique was presented in Section 1.3.
If
, are given in Figure 4.1.
In Figure 4.2 (left) we show the product of these two
densities.
The kernel density technique was presented in Section 1.3.
If 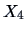 and
and 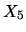 are independent, this product
are independent, this product
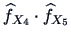 should be roughly equal to
should be roughly equal to
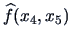 , the estimate of the joint density of
, the estimate of the joint density of
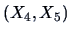 .
Comparing the two graphs in Figure 4.2
reveals that the two densities are different.
The two variables
.
Comparing the two graphs in Figure 4.2
reveals that the two densities are different.
The two variables 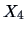 and
and 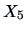 are therefore not independent.
are therefore not independent.
Figure 4.1:
Univariate estimates of the density of 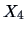 (left) and
(left) and 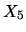 (right) of the bank notes.
(right) of the bank notes.
 MVAdenbank2.xpl
MVAdenbank2.xpl
|
|
Figure 4.2:
The product of univariate density estimates
(left) and the joint density estimate (right) for 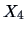 (left) and
(left) and 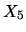 of the bank notes.
of the bank notes.
 MVAdenbank3.xpl
MVAdenbank3.xpl
|
|
An elegant concept of connecting marginals with joint cdfs is given by
copulas.
Copulas are important in Value-at-Risk calculations and
are an essential tool in quantitative finance (Härdle et al.; 2002).
For simplicity of presentation we concentrate on the 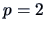 dimensional case.
A 2-dimensional copula is a function
dimensional case.
A 2-dimensional copula is a function
![$C: \, [0,1]^2 \to [0,1]$](mvahtmlimg1133.gif) with the following properties:
with the following properties:
The usage of the name ``copula'' for the function 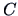 is explained by the
following theorem.
is explained by the
following theorem.
THEOREM 4.1 (Sklar's theorem)
Let
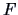
be a joint distribution function with marginal distribution
functions
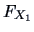
and
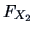
. Then there exists a copula
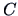
with
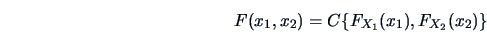 |
(4.5) |
for every
. If
and
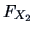
are
continuous, then
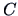
is unique.
On the other hand, if
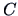
is a copula and
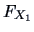
and
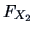
are distribution functions, then
the function
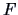
defined by (
4.5) is a joint distribution function
with marginals
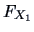
and
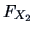
.
With Sklar's Theorem, the use of the name ``copula''
becomes obvious.
It was chosen to describe ``a function that
links a multidimensional distribution to its one-dimensional
margins'' and appeared in the mathematical literature for the first
time in Sklar (1959).
EXAMPLE 4.3
The
structure of independence implies that
the product of the distribution functions
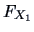
and
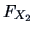
equals their joint distribution function
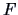
,
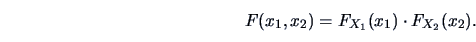 |
(4.6) |
Thus, we obtain the
independence copula
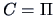
from
THEOREM 4.2
Let
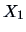
and
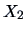
be random variables with continuous
distribution functions
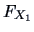
and
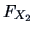
and the joint distribution
function
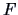
.
Then
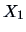
and
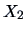
are independent if and only if
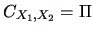
.
PROOF:
From Sklar's Theorem we know that there exists an
unique copula 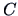 with
with
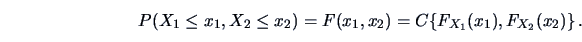 |
(4.7) |
Independence can be seen using (4.5) for the joint
distribution function 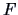 and the definition of
and the definition of  ,
,
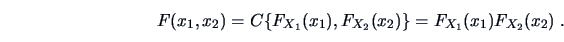 |
(4.8) |

EXAMPLE 4.4
The Gumbel-Hougaard family of
copulas (Nelsen; 1999) is given by the function
![\begin{displaymath}
C_{\theta}(u, v) = \exp \left\{ - \left[ (-\ln u)^{\theta}
+ (-\ln v)^{\theta} \right]^{1 / \theta} \right\} \; .
\end{displaymath}](mvahtmlimg1154.gif) |
(4.9) |
The parameter
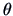
may take all values in the interval
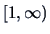
.
The Gumbel-Hougaard copulas are suited to describe bivariate extreme
value distributions.
For  , the expression (4.9)
reduces to the product copula, i.e.,
, the expression (4.9)
reduces to the product copula, i.e.,
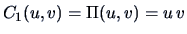 .
For
.
For
 one finds for the Gumbel-Hougaard copula:
one finds for the Gumbel-Hougaard copula:
where the function
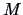
is also a copula such that
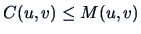
for
arbitrary copula
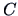
. The copula
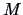
is called the
Fréchet-Hoeffding upper bound.
Similarly, we obtain the Fréchet-Hoeffding lower bound
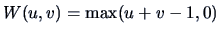 which satisfies
which satisfies
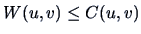 for any other copula
for any other copula 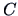 .
.
Summary

-
The cumulative distribution function (cdf) is defined as
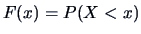 .
.

-
If a probability density function (pdf)
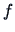 exists then
exists then
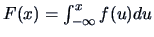 .
.

-
The pdf integrates to one, i.e.,
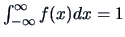 .
.

-
Let
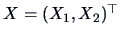 be partitioned into sub-vectors
be partitioned into sub-vectors 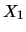 and
and
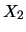 with joint cdf
with joint cdf 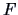 . Then
. Then
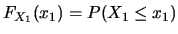 is the marginal cdf of
is the marginal cdf of
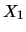 .
The marginal pdf of
.
The marginal pdf of 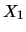 is obtained by
is obtained by
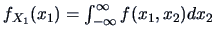 . Different joint pdf's
may have the same marginal pdf's.
. Different joint pdf's
may have the same marginal pdf's.

-
The conditional pdf of
 given
given  is defined as
is defined as
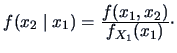

-
Two random variables
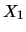 and
and 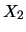 are called independent iff
are called independent iff
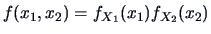 . This is equivalent to
. This is equivalent to
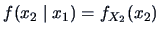 .
.

- Different joint pdf's may have identical marginal pdf's.



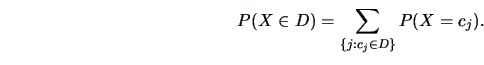
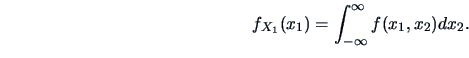

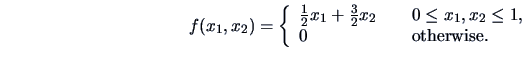
![\begin{displaymath}\int f(x_1,x_2) dx_1 dx_2 = \frac{1}{2} \left[
\frac{x^2_1}...
...
\frac{x^2_2}{2} \right]^1_0 = \frac{1}{4} + \frac{3}{4} = 1.\end{displaymath}](mvahtmlimg1113.gif)
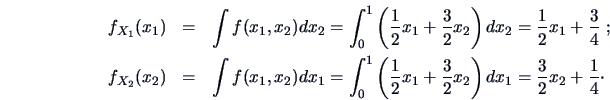
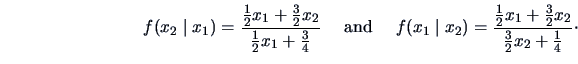
![]() and
and ![]() are independent if
the conditional pdf's are equal to the marginal
densities, i.e.,
are independent if
the conditional pdf's are equal to the marginal
densities, i.e.,
![]() and
and
![]() . Independence can be interpreted
as follows: knowing
. Independence can be interpreted
as follows: knowing ![]() does not change the probability assessments
on
does not change the probability assessments
on ![]() , and conversely.
, and conversely.
![]()
![\begin{displaymath}\int ^1_01+\alpha (2x_1-1)(2x_2-1)dx_2
=1+\alpha(2x_1-1)[x^2_2-x_2]^1_0=1. \end{displaymath}](mvahtmlimg1125.gif)
![]() (lower inner frame) and
(lower inner frame) and ![]() (upper
inner frame).
From Chapter 3, we already know that they
have significant correlation, so they are almost surely not independent.
Kernel estimates of the marginal densities,
(upper
inner frame).
From Chapter 3, we already know that they
have significant correlation, so they are almost surely not independent.
Kernel estimates of the marginal densities,
![]() and
and
![]() , are given in Figure 4.1.
In Figure 4.2 (left) we show the product of these two
densities.
The kernel density technique was presented in Section 1.3.
If
, are given in Figure 4.1.
In Figure 4.2 (left) we show the product of these two
densities.
The kernel density technique was presented in Section 1.3.
If ![]() and
and ![]() are independent, this product
are independent, this product
![]() should be roughly equal to
should be roughly equal to
![]() , the estimate of the joint density of
, the estimate of the joint density of
![]() .
Comparing the two graphs in Figure 4.2
reveals that the two densities are different.
The two variables
.
Comparing the two graphs in Figure 4.2
reveals that the two densities are different.
The two variables ![]() and
and ![]() are therefore not independent.
are therefore not independent.
![\includegraphics[width=1.3\defpicwidth]{MVAdenbank2.ps}](mvahtmlimg1131.gif)
![\includegraphics[width=1.3\defpicwidth]{MVAdenbank3.ps}](mvahtmlimg1132.gif)
![]() dimensional case.
A 2-dimensional copula is a function
dimensional case.
A 2-dimensional copula is a function
![]() with the following properties:
with the following properties:

![]() , the expression (4.9)
reduces to the product copula, i.e.,
, the expression (4.9)
reduces to the product copula, i.e.,
![]() .
For
.
For
![]() one finds for the Gumbel-Hougaard copula:
one finds for the Gumbel-Hougaard copula:
![]() which satisfies
which satisfies
![]() for any other copula
for any other copula ![]() .
.