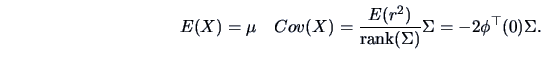5.4 Spherical and Elliptical Distributions
The multinormal distribution belongs to the large family of elliptical distributions
which has recently gained a lot of attention in financial mathematics. Elliptical distributions
are often used, particularly in risk management.
DEFINITION 5.1
A
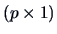
random vector
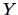
is said to have a spherical
distribution
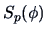
if its characteristic function
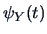
satisfies:
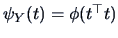
for some scalar function
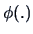
which is then called
the characteristic generator of the spherical distribution
.
We will write
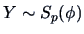
.
This is only one of several possible ways to define spherical distributions.
We can see spherical distributions as an extension of the standard multinormal
distribution
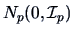 .
.
The random radius 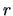 is related to the generator
is related to the generator 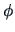 by a relation described
in Fang et al. (1990, p.29).
The moments of
by a relation described
in Fang et al. (1990, p.29).
The moments of
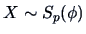 , provided that they exist, can be expressed
in terms of one-dimensional integrals (Fang et al.; 1990).
, provided that they exist, can be expressed
in terms of one-dimensional integrals (Fang et al.; 1990).
A spherically distributed random vector does not, in general, necessarily possess a density.
However, if it does, the marginal densities of dimension smaller than 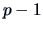 are continuous and the marginal
densities of dimension smaller than
are continuous and the marginal
densities of dimension smaller than 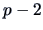 are differentiable (except possibly at the origin in
both cases).
Univariate marginal densities for
are differentiable (except possibly at the origin in
both cases).
Univariate marginal densities for  greater than
greater than 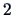 are nondecreasing on
are nondecreasing on 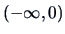 and
nonincreasing on
and
nonincreasing on 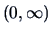 .
.
DEFINITION 5.2
A
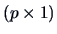
random vector

is said to have an elliptical
distribution
with parameters
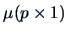
and
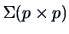
if

has the same distribution as
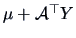
,
where
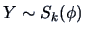
and
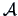
is a
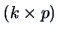
matrix such that
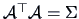
with
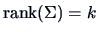
. We shall write
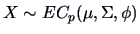
.
REMARK 5.1
The elliptical distribution can be seen as an extension of
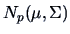
.
EXAMPLE 5.6
The multivariate t-distribution.
Let
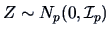
and
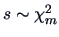
be independent. The random vector

has a multivariate
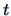
-distribution with
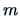
degrees of freedom.
Moreover the
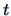
-distribution belongs to the family of p-dimensioned spherical distributions.
EXAMPLE 5.7
The multinormal distribution.
Let
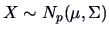
. Then
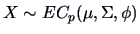
and
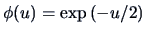
.
Figure
4.3 shows a density surface of the multivariate normal distribution:
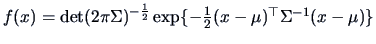
with
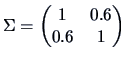
and
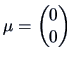
Notice that the density is constant on ellipses. This is the reason for calling
this family of distributions ``elliptical''.
![]() .
.
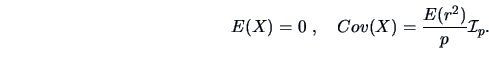
![]() is related to the generator
is related to the generator ![]() by a relation described
in Fang et al. (1990, p.29).
The moments of
by a relation described
in Fang et al. (1990, p.29).
The moments of
![]() , provided that they exist, can be expressed
in terms of one-dimensional integrals (Fang et al.; 1990).
, provided that they exist, can be expressed
in terms of one-dimensional integrals (Fang et al.; 1990).
![]() are continuous and the marginal
densities of dimension smaller than
are continuous and the marginal
densities of dimension smaller than ![]() are differentiable (except possibly at the origin in
both cases).
Univariate marginal densities for
are differentiable (except possibly at the origin in
both cases).
Univariate marginal densities for ![]() greater than
greater than ![]() are nondecreasing on
are nondecreasing on ![]() and
nonincreasing on
and
nonincreasing on ![]() .
.
 has a multivariate
has a multivariate 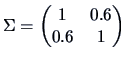 and
and
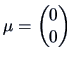 Notice that the density is constant on ellipses. This is the reason for calling
this family of distributions ``elliptical''.
Notice that the density is constant on ellipses. This is the reason for calling
this family of distributions ``elliptical''.