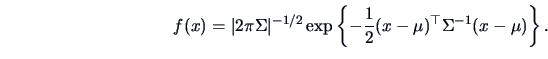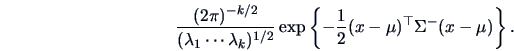The multinormal distribution with mean 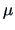 and covariance
and covariance 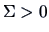 has the density
has the density
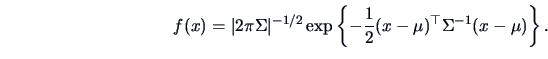 |
(4.47) |
We write
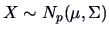 .
.
How is this multinormal distribution with mean 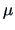 and covariance
and covariance
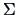 related to the multivariate standard normal
related to the multivariate standard normal
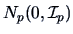 ?
Through a linear transformation
using the results of Section 4.3, as shown in the next theorem.
?
Through a linear transformation
using the results of Section 4.3, as shown in the next theorem.
THEOREM 4.5
Let
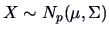
and
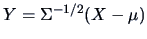
(Mahalanobis transformation
). Then
i.e., the elements
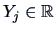
are independent, one-dimensional
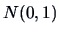
variables.
PROOF:
Note that
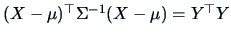 .
Application of (4.45) gives
.
Application of (4.45) gives
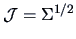 , hence
, hence
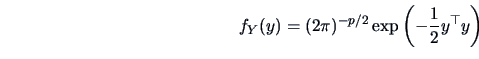 |
(4.48) |
which is by (4.47) the pdf of a
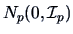 .
.

Note that
the above Mahalanobis transformation yields
in fact a random variable
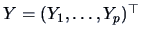 composed of independent
one-dimensional
composed of independent
one-dimensional
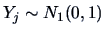 since
since
Here each 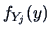 is a standard normal density
is a standard normal density
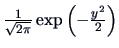 .
From this it is clear that
.
From this it is clear that 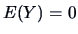 and
and
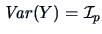 .
.
How can we create
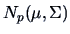 variables on the basis of
variables on the basis of
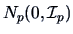 variables? We use the inverse linear transformation
variables? We use the inverse linear transformation
 |
(4.49) |
Using (4.11) and (4.23) we can also check that 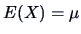 and
and
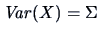 .
The following theorem is useful because it presents the distribution
of a variable after it has been linearly transformed.
The proof is left as an exercise.
.
The following theorem is useful because it presents the distribution
of a variable after it has been linearly transformed.
The proof is left as an exercise.
THEOREM 4.6
Let
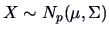
and
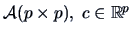
,
where
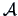
is nonsingular.
Then
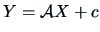 is again a
is again a  -variate Normal, i.e.,
-variate Normal, i.e.,
 |
(4.50) |
From (4.47) we see that the density of the
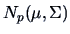 distribution
is constant on ellipsoids of the form
distribution
is constant on ellipsoids of the form
 |
(4.51) |
EXAMPLE 4.14
Figure
4.3 shows the contour ellipses of a
two-dimensional normal distribution. Note that these contour ellipses
are the iso-distance curves (
2.34) from the mean of
this normal distribution corresponding to the metric
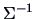
.
Figure 4.3:
Scatterplot
of a normal sample and contour ellipses for
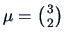 and
and
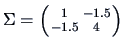 .
.
 MVAcontnorm.xpl
MVAcontnorm.xpl
|
|
According to Theorem 2.7 in Section 2.6 the
half-lengths of the axes in the contour
ellipsoid are
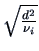 where
where
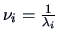 are
the eigenvalues of
are
the eigenvalues of 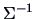 and
and 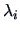 are the eigenvalues of
are the eigenvalues of
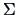 .
The rectangle inscribing an ellipse has sides with length
.
The rectangle inscribing an ellipse has sides with length 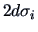 and is thus
naturally proportional to the standard deviations of
and is thus
naturally proportional to the standard deviations of 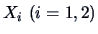 .
.
The distribution of the quadratic form in (4.51) is given in
the next theorem.
THEOREM 4.8
The characteristic function (cf) of a multinormal
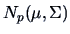
is given by
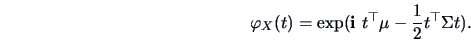 |
(4.52) |
We can check Theorem 4.8 by transforming the cf back:
since
Note that if
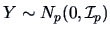 (e.g., the Mahalanobis-transform), then
(e.g., the Mahalanobis-transform), then
which is consistent with (4.33).
Singular Normal Distribution
Suppose that we have
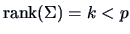 , where
, where  is
the dimension of
is
the dimension of  .
We define the (singular) density of
.
We define the (singular) density of  with the aid of the
with the aid of the 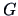 -Inverse
-Inverse
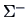 of
of 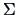 ,
,
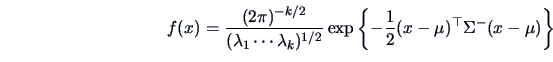 |
(4.53) |
where
- (1)
 lies on the hyperplane
lies on the hyperplane
 with
with
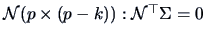 and
and
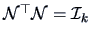 .
.
- (2)
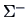 is the
is the  -Inverse of
-Inverse of 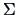 , and
, and
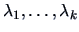 are the nonzero eigenvalues of
are the nonzero eigenvalues of 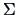 .
.
What is the connection to a multinormal with 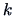 -dimensions? If
-dimensions? If
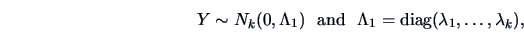 |
(4.54) |
then there exists an orthogonal matrix
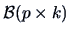 with
with
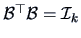 so that
so that
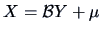 where
where  has a singular pdf of the form (4.53).
has a singular pdf of the form (4.53).
The second important copula that we want to present is the
Gaussian or normal copula,
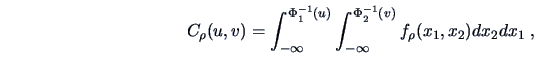 |
(4.55) |
see Embrechts et al. (1999). In (4.55), 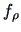 denotes the bivariate normal density
function with correlation
denotes the bivariate normal density
function with correlation 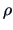 for
for 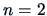 . The functions
. The functions 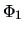 and
and 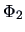 in (4.55) refer to the corresponding
one-dimensional standard normal cdfs of the margins.
in (4.55) refer to the corresponding
one-dimensional standard normal cdfs of the margins.
In the case of vanishing correlation, 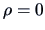 , the Gaussian copula becomes
, the Gaussian copula becomes
Summary

- The pdf of a
 -dimensional multinormal
-dimensional multinormal
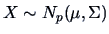 is
is
The contour curves of a multinormal are ellipsoids with half-lengths
proportional to
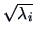 , where
, where 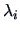 denotes the eigenvalues of
denotes the eigenvalues of 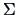 (
(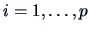 ).
).

-
The Mahalanobis transformation transforms
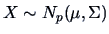 to
to
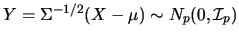 .
Going the other direction,
one can create a
.
Going the other direction,
one can create a
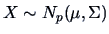 from
from
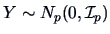 via
via
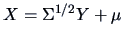 .
.

-
If the covariance matrix
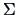 is singular (i.e.,
is singular (i.e.,
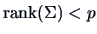 ),
then it defines a singular normal distribution.
),
then it defines a singular normal distribution.

-
The density of a singular normal distribution is given by
![]() and covariance
and covariance ![]() has the density
has the density
![]() and covariance
and covariance
![]() related to the multivariate standard normal
related to the multivariate standard normal
![]() ?
Through a linear transformation
using the results of Section 4.3, as shown in the next theorem.
?
Through a linear transformation
using the results of Section 4.3, as shown in the next theorem.
![]() .
Application of (4.45) gives
.
Application of (4.45) gives
![]() , hence
, hence
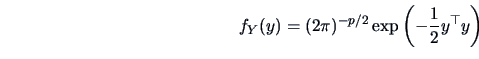
![]() composed of independent
one-dimensional
composed of independent
one-dimensional
![]() since
since
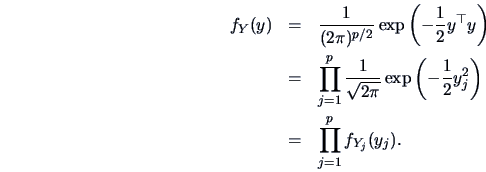
![]() variables on the basis of
variables on the basis of
![]() variables? We use the inverse linear transformation
variables? We use the inverse linear transformation
![]() distribution
is constant on ellipsoids of the form
distribution
is constant on ellipsoids of the form
![]() where
where
![]() are
the eigenvalues of
are
the eigenvalues of ![]() and
and ![]() are the eigenvalues of
are the eigenvalues of
![]() .
The rectangle inscribing an ellipse has sides with length
.
The rectangle inscribing an ellipse has sides with length ![]() and is thus
naturally proportional to the standard deviations of
and is thus
naturally proportional to the standard deviations of ![]() .
.
![\begin{eqnarray*}
f(x) & = & \frac{1}{(2\pi)^p} \int \exp\left(-{\bf i}t^{\top}x...
...} \exp\left[-\frac{1}{2}\{(x-\mu)^{\top}\Sigma
(x-\mu)\}\right]
\end{eqnarray*}](mvahtmlimg1412.gif)
![\begin{eqnarray*}
&&\int \frac{1}{\vert 2\pi\Sigma^{-1}\vert^{1/2}} \exp \left[-...
...top}\Sigma(t+{\bf i}\Sigma^{-1}(x-\mu))\}\right]\,dt \\
&&= 1.
\end{eqnarray*}](mvahtmlimg1413.gif)
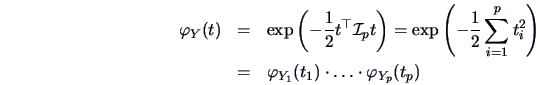
![]() , where
, where ![]() is
the dimension of
is
the dimension of ![]() .
We define the (singular) density of
.
We define the (singular) density of ![]() with the aid of the
with the aid of the ![]() -Inverse
-Inverse
![]() of
of ![]() ,
,
![]() , the Gaussian copula becomes
, the Gaussian copula becomes