4.2 Moments and Characteristic Functions
Moments--Expectation and Covariance Matrix
If  is a random vector with density
is a random vector with density
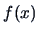 then the
expectation of
then the
expectation of  is
is
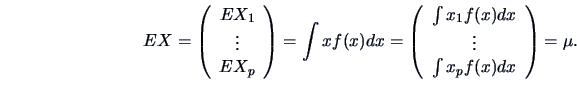 |
(4.10) |
Accordingly, the expectation of a matrix of random elements has to be understood
component by component.
The operation of forming expectations is linear:
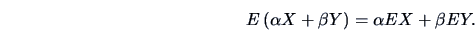 |
(4.11) |
If 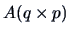 is a matrix of real numbers, we have:
is a matrix of real numbers, we have:
 |
(4.12) |
When  and
and 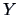 are independent,
are independent,
 |
(4.13) |
The matrix
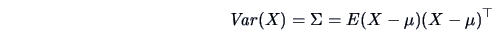 |
(4.14) |
is the (theoretical) covariance matrix.
We write for a vector  with mean vector
with mean vector 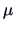 and covariance matrix
and covariance matrix
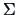 ,
,
 |
(4.15) |
The 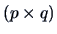 matrix
matrix
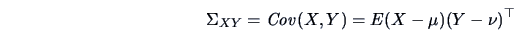 |
(4.16) |
is the covariance matrix of
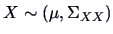 and
and
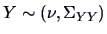 . Note that
. Note that
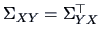 and
that
and
that
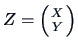 has covariance
has covariance
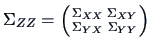 . From
. From
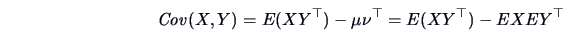 |
(4.17) |
it follows that 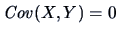 in the case where
in the case where  and
and 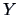 are independent.
We often say that
are independent.
We often say that 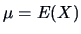 is the first order moment of
is the first order moment of  and that
and that
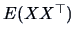 provides the second order moments of
provides the second order moments of  :
:
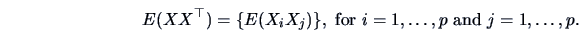 |
(4.18) |
Properties of the Covariance Matrix
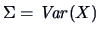
| |
|
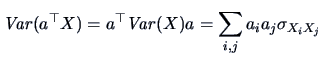 |
(4.22) |
| |
|
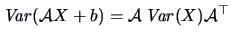 |
(4.23) |
| |
|
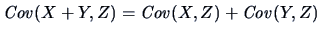 |
(4.24) |
| |
|
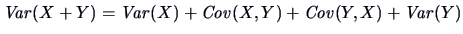 |
(4.25) |
| |
|
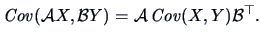 |
(4.26) |
Let us compute these quantities for a specific joint density.
EXAMPLE 4.5
Consider the pdf of Example
4.1.
The mean vector
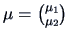
is
The elements of the covariance matrix are
Hence the covariance matrix is
Conditional Expectations
The conditional expectations are
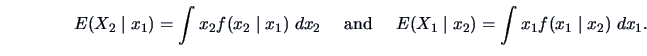 |
(4.27) |
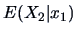 represents the location
parameter of the conditional pdf of
represents the location
parameter of the conditional pdf of 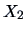 given that
given that 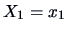 . In the same
way, we can define
. In the same
way, we can define
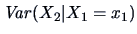 as a measure of the dispersion of
as a measure of the dispersion of
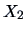 given that
given that 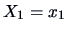 . We have from (4.20) that
. We have from (4.20) that
Using the conditional covariance matrix, the
conditional correlations may be defined as:
These conditional correlations are known as partial
correlations between 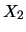 and
and
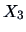 , conditioned on
, conditioned on 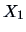 being equal to
being equal to 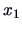 .
.
EXAMPLE 4.6
Consider the following pdf
Note that the pdf is symmetric in
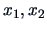
and
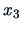
which facilitates the computations.
For instance,
and the other marginals are similar. We also have
It is easy to compute the following moments:
![$ E(X_i)=\frac{5}{9};\ E(X_i^2)=\frac{7}{18};\ E(X_iX_j)=\frac{11}{36}\ \ \left(...
...}\\ [3mm]
E(X_1X_2\vert X_3=x_3)=\frac{1}{12}\left(\frac{3x_3+4}{x_3+1}\right).$](mvahtmlimg1216.gif)
Note that the conditional means of 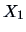 and of
and of 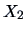 , given
, given 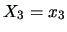 , are not linear in
, are not linear in 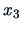 .
From these moments we obtain:
.
From these moments we obtain:
The conditional covariance matrix of
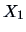
and
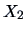
,
given
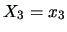
is
In particular, the partial correlation between
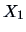
and
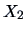
, given
that
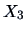
is fixed at
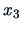
,
is given by

which ranges
from
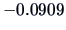
to
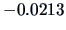
when
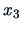
goes from 0 to 1. Therefore, in this example,
the partial correlation may be larger or smaller than the simple correlation, depending on the value
of the condition
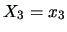
.
EXAMPLE 4.7
Consider the following joint pdf
Note the symmetry of
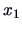
and
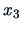
in the pdf and that
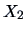
is independent
of
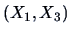
. It immediately follows that
Simple computations lead to
Let us analyze the conditional distribution of
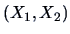
given
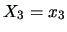
.
We have
so that again
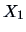
and
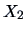
are independent conditional on
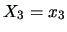
.
In this case
Since
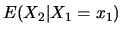 is a function of
is a function of 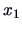 , say
, say 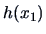 , we can define
the random variable
, we can define
the random variable
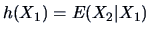 . The same can be done when defining
the random variable
. The same can be done when defining
the random variable 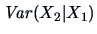 . These two
random variables share some interesting properties:
. These two
random variables share some interesting properties:
EXAMPLE 4.8
Consider the following pdf
It is easy to show that
Without explicitly computing
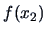
, we can obtain:
The conditional expectation 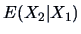 viewed as a function
viewed as a function 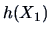 of
of
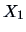 (known as the regression function of
(known as the regression function of 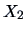 on
on 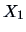 ), can be interpreted
as a conditional approximation of
), can be interpreted
as a conditional approximation of 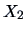 by a function of
by a function of 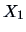 . The error term
of the approximation is then given by:
. The error term
of the approximation is then given by:
Characteristic Functions
The characteristic function (cf) of a random vector
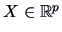 (respectively its density
(respectively its density 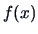 ) is defined as
) is defined as
where 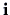 is the complex unit:
is the complex unit:
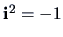 .
The cf has the following properties:
.
The cf has the following properties:
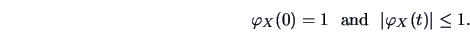 |
(4.30) |
If 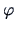 is absolutely integrable, i.e., the integral
is absolutely integrable, i.e., the integral
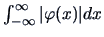 exists and is finite, then
exists and is finite, then
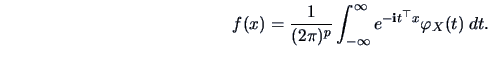 |
(4.31) |
If
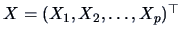 , then for
, then for
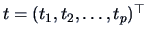
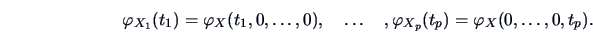 |
(4.32) |
If
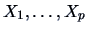 are independent random variables, then
for
are independent random variables, then
for
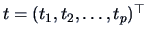
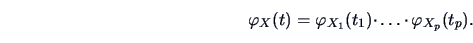 |
(4.33) |
If
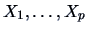 are independent random variables, then for
are independent random variables, then for
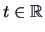
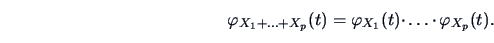 |
(4.34) |
The characteristic function can recover all the cross-product
moments of any order:
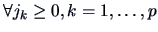 and for
and for
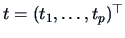 we have
we have
![\begin{displaymath}
E \left( X_1^{j_1}\cdotp\ldots\cdotp X_p^{j_p} \right) =
\fr...
...\partial t_1^{j_1} \ldots \partial t_p^{j_p} } \right]_{t=0}.
\end{displaymath}](mvahtmlimg1267.gif) |
(4.35) |
EXAMPLE 4.9
The cf of the density in example
4.5 is given by
EXAMPLE 4.10
Suppose
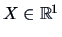
follows the density of the standard normal distribution
(see Section
4.4) then the cf can be computed via
since
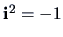
and
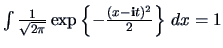
.
A variety of distributional characteristics can be computed from
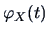 . The standard normal distribution has a very simple cf,
as was seen in Example 4.10. Deviations from normal covariance
structures can be measured by the deviations from the
cf (or characteristics of it). In Table 4.1 we give an
overview of the cf's for a variety of distributions.
. The standard normal distribution has a very simple cf,
as was seen in Example 4.10. Deviations from normal covariance
structures can be measured by the deviations from the
cf (or characteristics of it). In Table 4.1 we give an
overview of the cf's for a variety of distributions.
Table 4.1:
Characteristic functions for some common distributions.
|
|
THEOREM 4.4 (Cramer-Wold
)
The distribution of
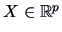
is completely determined by the set of all
(one-dimensional) distributions of
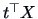
where
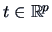
.
This theorem says that we can determine the distribution of  in
in
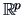 by specifying all of the one-dimensional distributions of the
linear combinations
by specifying all of the one-dimensional distributions of the
linear combinations
Cumulant functions
Moments
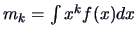 often help in describing distributional
characteristics. The normal distribution in
often help in describing distributional
characteristics. The normal distribution in 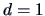 dimension is completely
characterized by its standard normal density
dimension is completely
characterized by its standard normal density 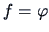 and the
moment parameters are
and the
moment parameters are
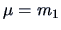 and
and
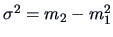 . Another helpful class of parameters are the cumulants or
semi-invariants of a distribution. In order to simplify notation we
concentrate here on the one-dimensional (
. Another helpful class of parameters are the cumulants or
semi-invariants of a distribution. In order to simplify notation we
concentrate here on the one-dimensional (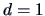 ) case.
) case.
For a given random variable  with density
with density 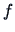 and finite
moments of order
and finite
moments of order 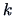 the characteristic function
the characteristic function
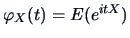 has the derivative
has the derivative
The values 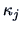 are called cumulants or semi-invariants since
are called cumulants or semi-invariants since
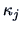 does not change (for
does not change (for 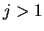 ) under a shift transformation
) under a shift transformation
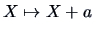 . The cumulants are natural parameters for dimension
reduction methods, in particular the Projection Pursuit method
(see Section 18.2).
. The cumulants are natural parameters for dimension
reduction methods, in particular the Projection Pursuit method
(see Section 18.2).
The relationship between the first 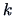 moments
moments 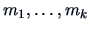 and the
cumulants is given by
and the
cumulants is given by
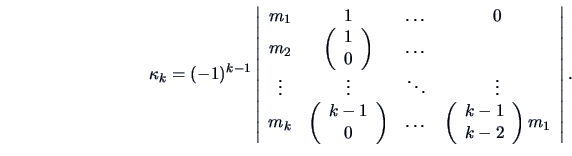 |
(4.36) |
EXAMPLE 4.11
Suppose that
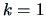
, then formula (
4.36) above yields
For
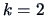
we obtain
For
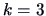
we have to calculate
Calculating the determinant we have:
Similarly one calculates
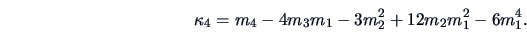 |
(4.38) |
The same type of process is used to find the moments of the cumulants:
A very simple relationship can be observed between the semi-invariants
and the central moments
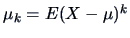 , where
, where 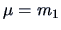 as
defined before. In fact,
as
defined before. In fact,
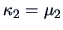 ,
,
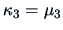 and
and
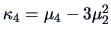 .
.
Skewness 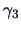 and kurtosis
and kurtosis 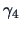 are defined as:
are defined as:
The skewness and kurtosis determine the shape of one-dimensional distributions.
The skewness of a normal distribution is 0 and the kurtosis equals 3.
The relation of these parameters to the cumulants is given by:
These relations will be used later in Section 18.2 on
Projection Pursuit to determine deviations from normality.
Summary

-
The expectation of a random vector
 is
is
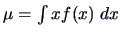 ,
the covariance matrix
,
the covariance matrix
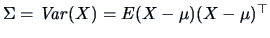 . We denote
. We denote
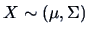 .
.

-
Expectations are linear, i.e.,
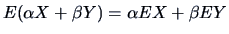 . If
. If  and
and 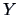 are
independent, then
are
independent, then
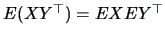 .
.

-
The covariance between two random vectors
 and
and 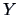 is
is
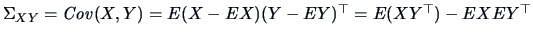 . If
. If  and
and
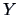 are independent, then
are independent, then 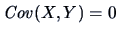 .
.

-
The characteristic function (cf) of a random vector
 is
is
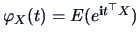 .
.

-
The distribution of a
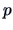 -dimensional random variable
-dimensional random variable  is
completely determined by all one-dimensional distributions of
is
completely determined by all one-dimensional distributions of 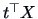 where
where
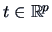 (Theorem of Cramer-Wold).
(Theorem of Cramer-Wold).

-
The conditional expectation
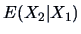 is the MSE best approximation
of
is the MSE best approximation
of 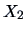 by a function of
by a function of 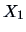 .
.
![]() is a random vector with density
is a random vector with density
![]() then the
expectation of
then the
expectation of ![]() is
is
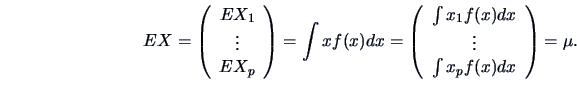
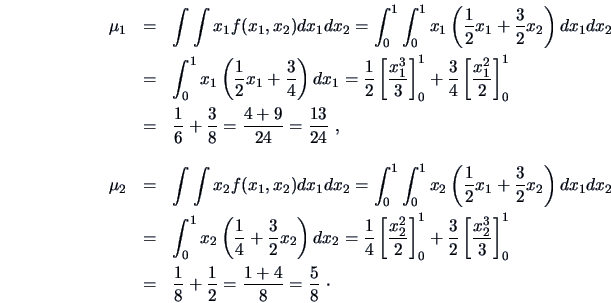
![\begin{eqnarray*}
\sigma_{X_{1}X_{1}} & = & EX^2_1 - \mu^2_1 \quad \textrm{ with...
...+ \frac{3}{4}
\left[ \frac{x^3_2}{3} \right]^1_0 = \frac{1}{3}.
\end{eqnarray*}](mvahtmlimg1203.gif)

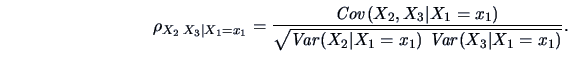
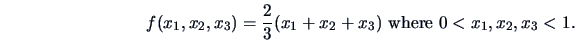
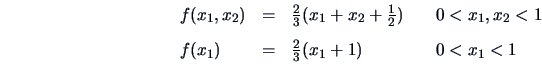
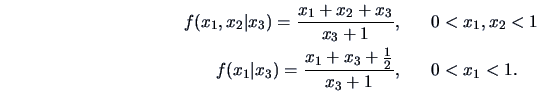
![]() and of
and of ![]() , given
, given ![]() , are not linear in
, are not linear in ![]() .
From these moments we obtain:
.
From these moments we obtain:
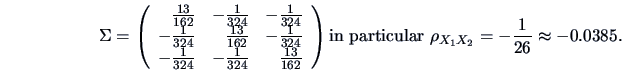
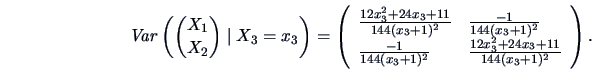

![\begin{displaymath}E(X)=\left(\begin{array}{c}
\frac{7}{12}\\ [3mm]
\frac{2}{3}\...
... 0\\
-\frac{1}{144} & 0 & \frac{11}{144}
\end{array}\right).\end{displaymath}](mvahtmlimg1227.gif)
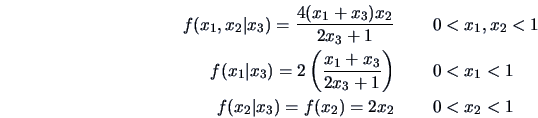
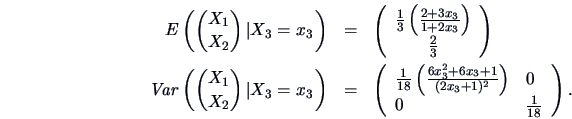
![]() is a function of
is a function of ![]() , say
, say ![]() , we can define
the random variable
, we can define
the random variable
![]() . The same can be done when defining
the random variable
. The same can be done when defining
the random variable ![]() . These two
random variables share some interesting properties:
. These two
random variables share some interesting properties:
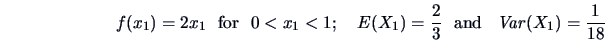
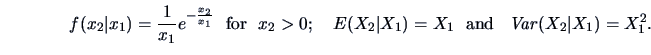
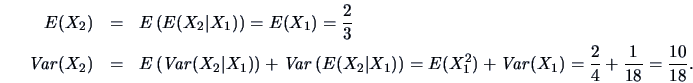
![]() viewed as a function
viewed as a function ![]() of
of
![]() (known as the regression function of
(known as the regression function of ![]() on
on ![]() ), can be interpreted
as a conditional approximation of
), can be interpreted
as a conditional approximation of ![]() by a function of
by a function of ![]() . The error term
of the approximation is then given by:
. The error term
of the approximation is then given by:
![]() (respectively its density
(respectively its density ![]() ) is defined as
) is defined as
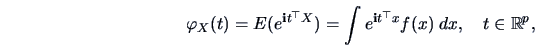
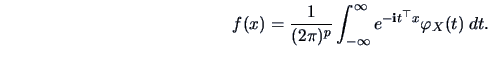
![\begin{displaymath}
E \left( X_1^{j_1}\cdotp\ldots\cdotp X_p^{j_p} \right) =
\fr...
...\partial t_1^{j_1} \ldots \partial t_p^{j_p} } \right]_{t=0}.
\end{displaymath}](mvahtmlimg1267.gif)

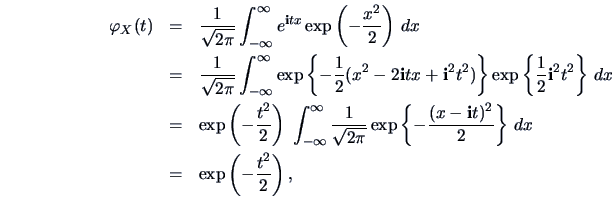
![]() . The standard normal distribution has a very simple cf,
as was seen in Example 4.10. Deviations from normal covariance
structures can be measured by the deviations from the
cf (or characteristics of it). In Table 4.1 we give an
overview of the cf's for a variety of distributions.
. The standard normal distribution has a very simple cf,
as was seen in Example 4.10. Deviations from normal covariance
structures can be measured by the deviations from the
cf (or characteristics of it). In Table 4.1 we give an
overview of the cf's for a variety of distributions.
![]() in
in
![]() by specifying all of the one-dimensional distributions of the
linear combinations
by specifying all of the one-dimensional distributions of the
linear combinations
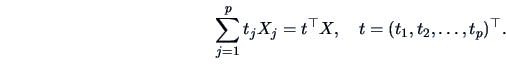
![]() often help in describing distributional
characteristics. The normal distribution in
often help in describing distributional
characteristics. The normal distribution in ![]() dimension is completely
characterized by its standard normal density
dimension is completely
characterized by its standard normal density ![]() and the
moment parameters are
and the
moment parameters are
![]() and
and
![]() . Another helpful class of parameters are the cumulants or
semi-invariants of a distribution. In order to simplify notation we
concentrate here on the one-dimensional (
. Another helpful class of parameters are the cumulants or
semi-invariants of a distribution. In order to simplify notation we
concentrate here on the one-dimensional (![]() ) case.
) case.
![]() with density
with density ![]() and finite
moments of order
and finite
moments of order ![]() the characteristic function
the characteristic function
![]() has the derivative
has the derivative
![\begin{displaymath}
\frac{1}{i^j}
\left[ \frac{\partial^j \varphi_X(t)}{\partial t^j }\right]_{t=0} = \kappa_j,
\qquad j=1,\dots,k.
\end{displaymath}](mvahtmlimg1294.gif)
![]() moments
moments ![]() and the
cumulants is given by
and the
cumulants is given by
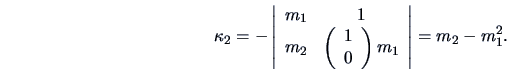

![]() and kurtosis
and kurtosis ![]() are defined as:
are defined as: