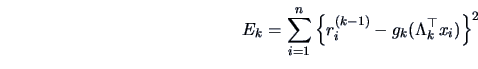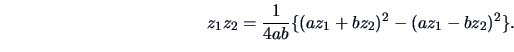18.2 Projection Pursuit
``Projection Pursuit'' stands for a
class of exploratory projection techniques. This class contains
statistical methods designed for analyzing high-dimensional data using
low-dimensional projections.
The aim of projection pursuit is to reveal possible nonlinear
and therefore interesting structures
hidden in the high-dimensional data. To what extent these
structures are ``interesting'' is measured by an index.
Exploratory Projection Pursuit (EPP) goes back to
Kruskal(1972,1969). The approach was
successfully implemented for exploratory purposes by various other authors.
The idea has been applied to regression analysis, density estimation,
classification and discriminant analysis.
Exploratory Projection Pursuit
In EPP, we try to find ``interesting'' low-dimensional projections of
the data. For this purpose, a suitable index function 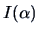 ,
depending on a normalized projection vector
,
depending on a normalized projection vector 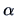 , is used.
This function will be defined such that ``interesting'' views correspond to
local and global maxima of the function.
This approach naturally accompanies the technique
of principal component analysis (PCA) of the covariance structure of
a random vector
, is used.
This function will be defined such that ``interesting'' views correspond to
local and global maxima of the function.
This approach naturally accompanies the technique
of principal component analysis (PCA) of the covariance structure of
a random vector  .
In PCA we are interested in finding the axes of the covariance
ellipsoid.
The index function
.
In PCA we are interested in finding the axes of the covariance
ellipsoid.
The index function 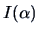 is in this case the variance
of a linear combination
is in this case the variance
of a linear combination
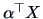 subject to the normalizing constraint
subject to the normalizing constraint
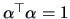 (see Theorem 9.2).
If we analyze a sample with a
(see Theorem 9.2).
If we analyze a sample with a  -dimensional normal distribution,
the ``interesting'' high-dimensional structure we find by
maximizing this index is of course linear.
-dimensional normal distribution,
the ``interesting'' high-dimensional structure we find by
maximizing this index is of course linear.
There are many possible projection indices, for simplicity the
kernel based and polynomial based indices are reported.
Assume that the  -dimensional random variable
-dimensional random variable  is
sphered and centered, that is,
is
sphered and centered, that is, 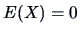 and
and
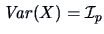 . This
will remove the effect of location, scale, and correlation structure.
This covariance structure can be achieved easily by the Mahalanobis
transformation (3.26).
. This
will remove the effect of location, scale, and correlation structure.
This covariance structure can be achieved easily by the Mahalanobis
transformation (3.26).
Friedman and Tukey (1974) proposed to investigate the high-dimensional distribution of  by considering the index
by considering the index
where
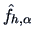 denotes the kernel estimator (see Section 1.3)
denotes the kernel estimator (see Section 1.3)
of the projected data. Note that (18.5) is an estimate of
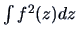 where
where
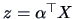 is a one-dimensional random variable with
mean zero and unit variance.
If the high-dimensional distribution of
is a one-dimensional random variable with
mean zero and unit variance.
If the high-dimensional distribution of  is normal,
then each projection
is normal,
then each projection
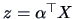 is standard normal
since
is standard normal
since 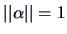 and since
and since
 has been centered and sphered by, e.g., the Mahalanobis transformation.
has been centered and sphered by, e.g., the Mahalanobis transformation.
The index should therefore be stable as a function of 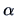 if the high-dimensional
data is in fact normal.
Changes in
if the high-dimensional
data is in fact normal.
Changes in
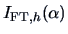 with respect to
with respect to 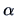 therefore indicate deviations from normality.
Hodges and Lehman (1956) showed that, given a
mean of zero and unit variance, the (compact support)
density which minimizes
therefore indicate deviations from normality.
Hodges and Lehman (1956) showed that, given a
mean of zero and unit variance, the (compact support)
density which minimizes 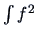 is uniquely given by
is uniquely given by
where
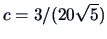 and
and 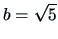 .
This is a parabolic density function,
which is equal to zero outside
the interval (
.
This is a parabolic density function,
which is equal to zero outside
the interval (
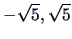 ).
A high value of the Friedman-Tukey index indicates
a larger departure from the parabolic form.
).
A high value of the Friedman-Tukey index indicates
a larger departure from the parabolic form.
An alternative index is based on the negative of the entropy measure,
i.e.,
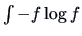 . The
density for zero mean and unit variance which minimizes the index
. The
density for zero mean and unit variance which minimizes the index
is the standard normal density, a far more plausible candidate than the parabolic density as a
norm from which departure is to be regarded as ``interesting''. Thus in using 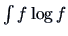 as
a projection index we are really implementing the viewpoint of seeing ``interesting'' projections as
departures from normality. Yet another index could be based on the Fisher information (see Section 6.2)
as
a projection index we are really implementing the viewpoint of seeing ``interesting'' projections as
departures from normality. Yet another index could be based on the Fisher information (see Section 6.2)
To optimize the entropy index, it is necessary to recalculate it at each step of the
numerical procedure. There is no method of obtaining the index via summary statistics
of the multivariate data set, so the workload of the calculation at each iteration is
determined by the number of observations. It is therefore interesting to look for
approximations to the entropy index.
Jones and Sibson (1987) suggested that deviations
from the normal density should be considered as
 |
(18.7) |
where the function 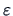 satisfies
satisfies
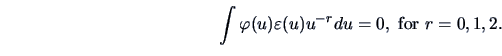 |
(18.8) |
In order to develop the Jones and Sibson index it is convenient to think in terms of cumulants
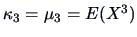 ,
,
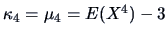 (see Section 4.2). The standard normal density
satisfies
(see Section 4.2). The standard normal density
satisfies
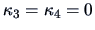 , an index with any hope of tracking the entropy index
must at least incorporate information up to the level of symmetric departures (
, an index with any hope of tracking the entropy index
must at least incorporate information up to the level of symmetric departures (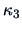 or
or 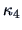 not zero) from normality. The simplest
of such indices is a positive definite quadratic
form in
not zero) from normality. The simplest
of such indices is a positive definite quadratic
form in 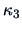 and
and 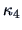 . It must be invariant under sign-reversal of the data since
both
. It must be invariant under sign-reversal of the data since
both
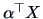 and
and
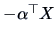 should show the same kind of departure from normality. Note that
should show the same kind of departure from normality. Note that
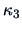 is odd under sign-reversal, i.e.,
is odd under sign-reversal, i.e.,
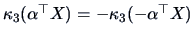 .
The cumulant
.
The cumulant 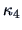 is even under sign-reversal, i.e.,
is even under sign-reversal, i.e.,
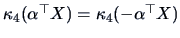 .
The quadratic form in
.
The quadratic form in 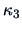 and
and 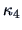 measuring departure
from normality cannot include a mixed
measuring departure
from normality cannot include a mixed
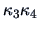 term.
term.
For the density (18.7) one may conclude with (18.8) that
Now if 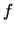 is expressed as a Gram-Charliér expansion
is expressed as a Gram-Charliér expansion
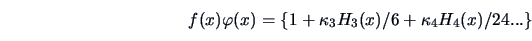 |
(18.9) |
(Kendall and Stuart; 1977, p. 169) where 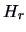 is the
is the 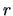 -th Hermite polynomial, then the
truncation of (18.9) and use of orthogonality and normalization properties of
Hermite polynomials with respect to
-th Hermite polynomial, then the
truncation of (18.9) and use of orthogonality and normalization properties of
Hermite polynomials with respect to 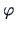 yields
yields
The index proposed by Jones and Sibson (1987) is therefore
This index measures in fact the difference
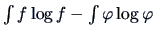 .
.
EXAMPLE 18.1
The exploratory Projection Pursuit is used on the Swiss bank note data.
For 50 randomly chosen one-dimensional projections of this
six-dimensional dataset we calculate the
Friedman-Tukey index to evaluate how ``interesting'' their structures are.
Figure:
Exploratory Projection Pursuit for the Swiss bank notes data
(green = standard normal, red = best, blue = worst).
 MVAppexample.xpl
MVAppexample.xpl
|
|
Figure 18.3 shows the density for the standard,
normally distributed data (green) and the estimated
densities for the best (red) and the worst (blue)
projections found. A dotplot of the projections is also presented.
In the lower part of the figure we see the
estimated value of the Friedman-Tukey index for each computed projection.
From this information we can judge the non normality of the bank note data set
since there is a lot of variation across the 50 random projections.
Projection Pursuit Regression
The problem in projection pursuit regression is to estimate a response surface
via approximating functions of the form
with non-parametric regression functions 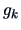 .
Given observations
.
Given observations
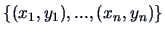 with
with
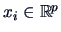 and
and
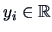 the basic algorithm works as follows.
the basic algorithm works as follows.
- Set
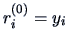 and
and 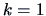 .
.
- Minimize
where 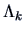 is an orthogonal projection matrix and
is an orthogonal projection matrix and 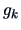 is a
non-parametric regression estimator.
is a
non-parametric regression estimator.
- Compute new residuals
- Increase
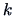 and repeat the last two steps until
and repeat the last two steps until 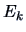 becomes
small.
becomes
small.
Although this approach seems to be simple, we encounter some problems.
One of the most serious is that the decomposition of a function into
sums of functions of projections may not be unique. An
example is
Improvements of this algorithm were suggested by Friedman and Stuetzle (1981).
Summary

-
Exploratory Projection Pursuit is a technique used
to find interesting structures in
high-dimensional data via low-dimensional projections. Since the
Gaussian distribution represents a standard situation, we define the
Gaussian distribution as the most uninteresting.

-
The search for interesting structures is done via a projection score like the
Friedman-Tukey index
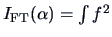 .
The parabolic distribution
has the minimal score. We maximize this score over all projections.
.
The parabolic distribution
has the minimal score. We maximize this score over all projections.

-
The Jones-Sibson index maximizes
as a function of 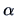 .
.

-
The entropy index maximizes
where 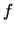 is the density of
is the density of
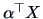 .
.

-
In Projection Pursuit Regression the idea is to
represent the unknown function by a sum of non-parametric regression functions
on projections. The key problem is in choosing the number of terms and often
the interpretability.
![]() ,
depending on a normalized projection vector
,
depending on a normalized projection vector ![]() , is used.
This function will be defined such that ``interesting'' views correspond to
local and global maxima of the function.
This approach naturally accompanies the technique
of principal component analysis (PCA) of the covariance structure of
a random vector
, is used.
This function will be defined such that ``interesting'' views correspond to
local and global maxima of the function.
This approach naturally accompanies the technique
of principal component analysis (PCA) of the covariance structure of
a random vector ![]() .
In PCA we are interested in finding the axes of the covariance
ellipsoid.
The index function
.
In PCA we are interested in finding the axes of the covariance
ellipsoid.
The index function ![]() is in this case the variance
of a linear combination
is in this case the variance
of a linear combination
![]() subject to the normalizing constraint
subject to the normalizing constraint
![]() (see Theorem 9.2).
If we analyze a sample with a
(see Theorem 9.2).
If we analyze a sample with a ![]() -dimensional normal distribution,
the ``interesting'' high-dimensional structure we find by
maximizing this index is of course linear.
-dimensional normal distribution,
the ``interesting'' high-dimensional structure we find by
maximizing this index is of course linear.
![]() -dimensional random variable
-dimensional random variable ![]() is
sphered and centered, that is,
is
sphered and centered, that is, ![]() and
and
![]() . This
will remove the effect of location, scale, and correlation structure.
This covariance structure can be achieved easily by the Mahalanobis
transformation (3.26).
. This
will remove the effect of location, scale, and correlation structure.
This covariance structure can be achieved easily by the Mahalanobis
transformation (3.26).
![]() by considering the index
by considering the index
![]() if the high-dimensional
data is in fact normal.
Changes in
if the high-dimensional
data is in fact normal.
Changes in
![]() with respect to
with respect to ![]() therefore indicate deviations from normality.
Hodges and Lehman (1956) showed that, given a
mean of zero and unit variance, the (compact support)
density which minimizes
therefore indicate deviations from normality.
Hodges and Lehman (1956) showed that, given a
mean of zero and unit variance, the (compact support)
density which minimizes ![]() is uniquely given by
is uniquely given by
![]() . The
density for zero mean and unit variance which minimizes the index
. The
density for zero mean and unit variance which minimizes the index


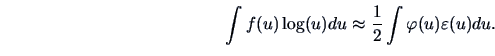
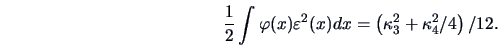
![% latex2html id marker 77827
\includegraphics[width=1\defpicwidth]{ppexample.ps}](mvahtmlimg4258.gif)