6.2 The Cramer-Rao Lower Bound
As pointed out above, an important question in estimation theory is whether an
estimator
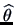 has certain desired properties,
in particular, if it
converges to the unknown parameter
has certain desired properties,
in particular, if it
converges to the unknown parameter  it is supposed to
estimate. One typical property we want for an estimator is unbiasedness,
meaning that on the average, the estimator hits its target:
it is supposed to
estimate. One typical property we want for an estimator is unbiasedness,
meaning that on the average, the estimator hits its target:
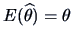 . We have seen for instance (see Example 6.2) that
. We have seen for instance (see Example 6.2) that
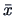 is an unbiased estimator of
is an unbiased estimator of 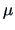 and
and 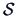 is a biased
estimator of
is a biased
estimator of 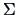 in finite samples.
If we restrict ourselves to unbiased estimation then the natural question is
whether the estimator shares some optimality properties in terms of its
sampling variance. Since
we focus on unbiasedness, we look for an estimator with the smallest possible
variance.
in finite samples.
If we restrict ourselves to unbiased estimation then the natural question is
whether the estimator shares some optimality properties in terms of its
sampling variance. Since
we focus on unbiasedness, we look for an estimator with the smallest possible
variance.
In this context, the Cramer-Rao lower bound will give the minimal achievable
variance for any unbiased estimator. This result is valid under very general
regularity conditions (discussed below). One of the most important
applications of the Cramer-Rao lower bound is that it provides
the asymptotic optimality property of maximum likelihood
estimators. The Cramer-Rao theorem involves the score function and its
properties which will be derived first.
The score function
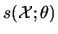 is the derivative of the
log likelihood function w.r.t.
is the derivative of the
log likelihood function w.r.t.
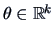
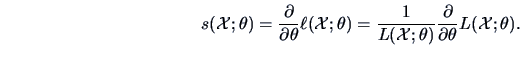 |
(6.9) |
The covariance matrix
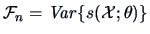 is called the
Fisher information matrix.
In what follows, we will give some interesting properties of score functions.
is called the
Fisher information matrix.
In what follows, we will give some interesting properties of score functions.
THEOREM 6.1
If
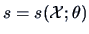
is the score function and if
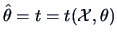
is any function of

and

, then
under regularity conditions
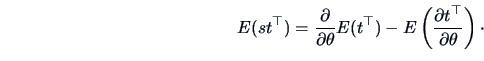 |
(6.10) |
The proof is left as an exercise (see Exercise 6.9).
The regularity conditions required for this theorem
are rather technical and ensure that the expressions
(expectations and derivations) appearing in (6.10) are well defined.
In particular, the support of the density 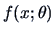 should not
depend on
should not
depend on  . The next corollary is a direct consequence.
. The next corollary is a direct consequence.
COROLLARY 6.1
If
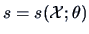
is the score
function, and
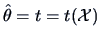
is any unbiased estimator of

(i.e.,
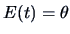
), then
 |
(6.11) |
Note that the score function has mean zero
(see Exercise 6.10).
 |
(6.12) |
Hence,
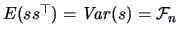 and by setting
and by setting 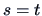 in Theorem 6.1 it follows that
in Theorem 6.1 it follows that
REMARK 6.1
If
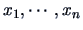
are i.i.d.,
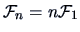
where
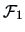
is
the Fisher information matrix for sample size n=1.
EXAMPLE 6.4
Consider an i.i.d. sample
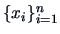
from
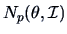
.
In this case the parameter

is the mean
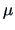
.
It follows from (
6.3) that:
Hence, the information matrix
is
How well can we estimate  ? The answer is given in the
following theorem which is due to Cramer and Rao. As pointed out above, this
theorem gives a lower bound for unbiased estimators. Hence, all estimators,
which are unbiased and attain this lower bound,
are minimum variance estimators.
? The answer is given in the
following theorem which is due to Cramer and Rao. As pointed out above, this
theorem gives a lower bound for unbiased estimators. Hence, all estimators,
which are unbiased and attain this lower bound,
are minimum variance estimators.
THEOREM 6.2 (Cramer-Rao
)
If
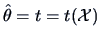
is any unbiased estimator
for

, then under regularity conditions
 |
(6.13) |
where
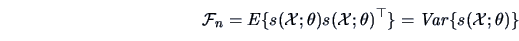 |
(6.14) |
is the Fisher information matrix
.
PROOF:
Consider the correlation  between
between 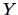 and
and 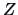 where
where 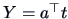 ,
,
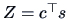 .
Here
.
Here 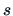 is the score and the vectors
is the score and the vectors 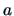 ,
,
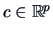 .
By Corollary 6.1
.
By Corollary 6.1
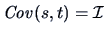 and thus
and thus
Hence,
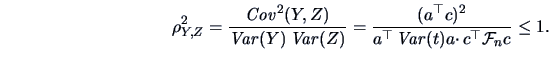 |
(6.15) |
In particular, this holds for any 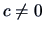 . Therefore it holds also for
the maximum of the left-hand side of (6.15) with respect to
. Therefore it holds also for
the maximum of the left-hand side of (6.15) with respect to 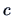 . Since
. Since
and
by our maximization Theorem 2.5 we have
i.e.,
which is equivalent to
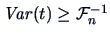 .
.

Maximum likelihood estimators (MLE's) attain the lower bound if the
sample size 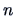 goes to infinity. The next Theorem 6.3
states this and, in addition,
gives the asymptotic sampling distribution
of the maximum likelihood estimation,
which turns out to be multinormal.
goes to infinity. The next Theorem 6.3
states this and, in addition,
gives the asymptotic sampling distribution
of the maximum likelihood estimation,
which turns out to be multinormal.
THEOREM 6.3
Suppose that the sample
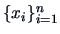
is i.i.d.
If
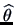
is the MLE for
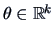
, i.e.,
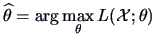
,
then under some regularity conditions, as
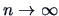
:
 |
(6.16) |
where
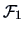
denotes the Fisher information
for sample size
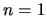
.
As a consequence of Theorem 6.3 we see that under regularity
conditions the MLE is asymptotically unbiased, efficient (minimum variance)
and normally distributed.
Also it is a consistent estimator of  .
.
Note that from property (5.4) of the multinormal it follows
that asymptotically
 |
(6.17) |
If
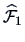 is a consistent estimator of
is a consistent estimator of
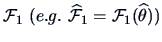 , we have equivalently
, we have equivalently
 |
(6.18) |
This expression is sometimes useful in testing hypotheses about  and in constructing confidence regions for
and in constructing confidence regions for  in a very general setup.
These issues will be raised in more details in the next chapter but
from (6.18) it can be seen, for instance, that when
in a very general setup.
These issues will be raised in more details in the next chapter but
from (6.18) it can be seen, for instance, that when 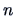 is large,
is large,
where
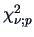 denotes the
denotes the 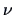 -quantile of a
-quantile of a 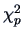 random variable. So, the ellipsoid
random variable. So, the ellipsoid
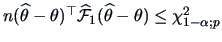 provides in
provides in 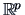 an asymptotic
an asymptotic 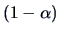 -confidence region for
-confidence region for  .
.
Summary

-
The score function is the derivative
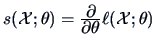 of the log-likelihood with
respect to
of the log-likelihood with
respect to  . The covariance matrix of
. The covariance matrix of
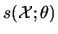 is
the Fisher information matrix.
is
the Fisher information matrix.

-
The score function has mean zero:
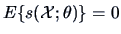 .
.

-
The Cramer-Rao bound says that any unbiased estimator
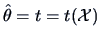 has a variance that is bounded
from below by the inverse of the Fisher information. Thus, an unbiased
estimator, which attains this lower bound, is a minimum variance estimator.
has a variance that is bounded
from below by the inverse of the Fisher information. Thus, an unbiased
estimator, which attains this lower bound, is a minimum variance estimator.

-
For i.i.d. data
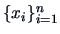 the Fisher information matrix is:
the Fisher information matrix is:
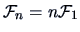 .
.

-
MLE's attain the lower bound in an asymptotic sense, i.e.,
if
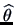 is the MLE for
is the MLE for
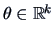 ,
i.e.,
,
i.e.,
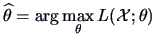 .
.
![]() has certain desired properties,
in particular, if it
converges to the unknown parameter
has certain desired properties,
in particular, if it
converges to the unknown parameter ![]() it is supposed to
estimate. One typical property we want for an estimator is unbiasedness,
meaning that on the average, the estimator hits its target:
it is supposed to
estimate. One typical property we want for an estimator is unbiasedness,
meaning that on the average, the estimator hits its target:
![]() . We have seen for instance (see Example 6.2) that
. We have seen for instance (see Example 6.2) that
![]() is an unbiased estimator of
is an unbiased estimator of ![]() and
and ![]() is a biased
estimator of
is a biased
estimator of ![]() in finite samples.
If we restrict ourselves to unbiased estimation then the natural question is
whether the estimator shares some optimality properties in terms of its
sampling variance. Since
we focus on unbiasedness, we look for an estimator with the smallest possible
variance.
in finite samples.
If we restrict ourselves to unbiased estimation then the natural question is
whether the estimator shares some optimality properties in terms of its
sampling variance. Since
we focus on unbiasedness, we look for an estimator with the smallest possible
variance.
![]() is the derivative of the
log likelihood function w.r.t.
is the derivative of the
log likelihood function w.r.t.
![]()
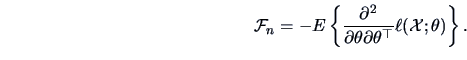
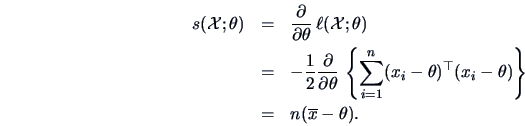
![]() ? The answer is given in the
following theorem which is due to Cramer and Rao. As pointed out above, this
theorem gives a lower bound for unbiased estimators. Hence, all estimators,
which are unbiased and attain this lower bound,
are minimum variance estimators.
? The answer is given in the
following theorem which is due to Cramer and Rao. As pointed out above, this
theorem gives a lower bound for unbiased estimators. Hence, all estimators,
which are unbiased and attain this lower bound,
are minimum variance estimators.
![]() between
between ![]() and
and ![]() where
where ![]() ,
,
![]() .
Here
.
Here ![]() is the score and the vectors
is the score and the vectors ![]() ,
,
![]() .
By Corollary 6.1
.
By Corollary 6.1
![]() and thus
and thus
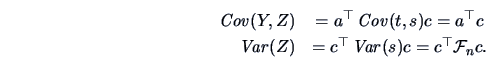
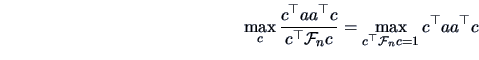

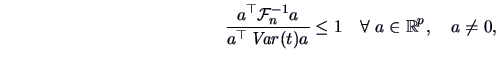
![]() goes to infinity. The next Theorem 6.3
states this and, in addition,
gives the asymptotic sampling distribution
of the maximum likelihood estimation,
which turns out to be multinormal.
goes to infinity. The next Theorem 6.3
states this and, in addition,
gives the asymptotic sampling distribution
of the maximum likelihood estimation,
which turns out to be multinormal.