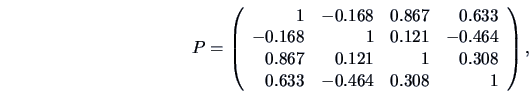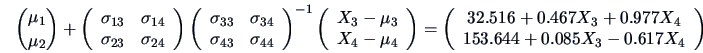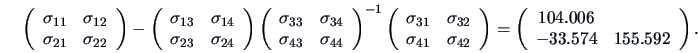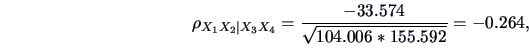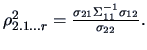Let us first summarize some properties which were
already derived in the previous chapter.
Often it is interesting to partition  into sub-vectors
into sub-vectors
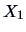 and
and 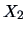 . The following theorem tells us how to correct
. The following theorem tells us how to correct
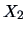 to obtain a vector which is independent of
to obtain a vector which is independent of 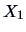 .
.
THEOREM 5.1
Let
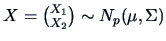
,
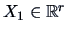
,
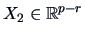
. Define
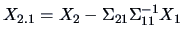
from the partitioned covariance matrix
Then
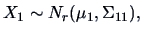 |
|
|
(5.5) |
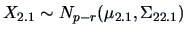 |
|
|
(5.6) |
are independent with
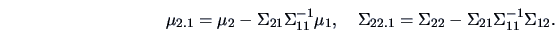 |
(5.7) |
PROOF:
Then, by (5.2)  and
and 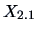 are both normal. Note that
are both normal. Note that
Recall that
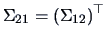 .
Hence
.
Hence
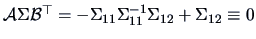 !
!
Using (5.2) again we also have the joint distribution of (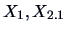 ), namely
), namely
With this block diagonal structure of the covariance matrix, the joint pdf of
(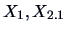 ) can easily be factorized into
) can easily be factorized into
from which the independence between  and
and 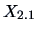 follows.
follows.
The next two corollaries are direct consequences of Theorem 5.1.
The independence of two linear transforms of a multinormal  can be
shown via the following corollary.
can be
shown via the following corollary.
COROLLARY 5.2
If
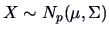
and given some matrices
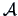
and
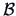
, then
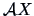
and
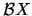
are independent if and only if
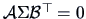
.
The following theorem is also useful. It generalizes Theorem 4.6.
The proof is left as an exercise.
THEOREM 5.2
If
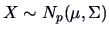
,
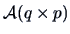
,
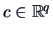
and
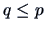
, then
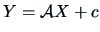
is a
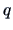
-variate Normal, i.e.,
The conditional distribution of
 given
given  is given by the next theorem.
is given by the next theorem.
THEOREM 5.3
The conditional distribution
of

given
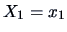
is normal with mean
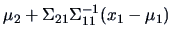
and covariance
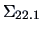
, i.e.,
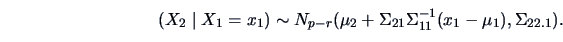 |
(5.8) |
PROOF:
Since
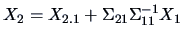 ,
for a fixed value of
,
for a fixed value of 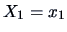 ,
,  is equivalent to
is equivalent to 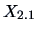 plus
a constant term:
plus
a constant term:
which has the normal distribution
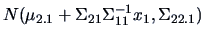 .
.
Note that the conditional mean of 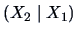 is a linear function of
is a linear function of
 and that the conditional variance does not depend on the particular
value of
and that the conditional variance does not depend on the particular
value of  . In the following example we consider a specific distribution.
. In the following example we consider a specific distribution.
EXAMPLE 5.1
Suppose that
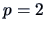
,

,
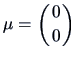
and
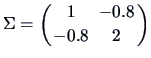
.
Then
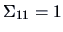
,

and
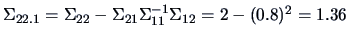
.
Hence the marginal pdf of

is
and the conditional pdf of
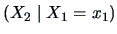
is given by
As mentioned above, the conditional mean of
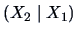
is linear in
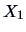
. The shift in the density of
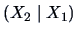
can be seen in
Figure
5.1.
Sometimes it will be useful to reconstruct a joint distribution from
the marginal distribution of  and the conditional distribution
and the conditional distribution 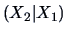 . The following theorem
shows under which conditions this can be easily done in the multinormal
framework.
. The following theorem
shows under which conditions this can be easily done in the multinormal
framework.
THEOREM 5.4
If
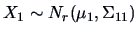
and
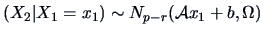
where
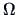
does not depend on
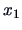
, then
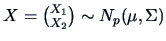
, where
EXAMPLE 5.2
Consider the following random variables
Using Theorem (
5.4), where
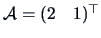
,
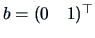
and
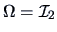
, we easily obtain the following result:
In particular, the marginal distribution of

is
thus conditional on

, the two components of

are independent but
marginally they are not!
Note that the marginal mean vector and covariance matrix of  could have
also been computed directly by using (4.28)-(4.29).
Using the derivation above, however, provides us with useful properties:
we have multinormality!
could have
also been computed directly by using (4.28)-(4.29).
Using the derivation above, however, provides us with useful properties:
we have multinormality!
Conditional Approximations
As we saw in Chapter 4 (Theorem 4.3), the
conditional expectation 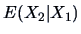 is the mean squared error (MSE) best
approximation of
is the mean squared error (MSE) best
approximation of  by a function of
by a function of  . We have in this case that
. We have in this case that
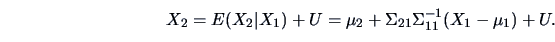 |
(5.9) |
Hence, the best approximation of
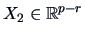 by
by
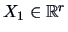 is the
linear approximation that can be written as:
is the
linear approximation that can be written as:
 |
(5.10) |
with
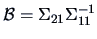 ,
,
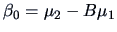 and
and
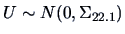 .
.
Consider now the particular case where 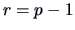 . Now
. Now
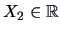 and
and
 is a row vector
is a row vector 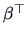 of dimension
of dimension 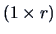
 |
(5.11) |
This means, geometrically speaking, that
the best MSE approximation of  by a function of
by a function of  is hyperplane.
The marginal variance of
is hyperplane.
The marginal variance of  can be decomposed via (5.11):
can be decomposed via (5.11):
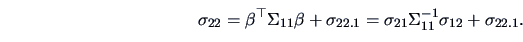 |
(5.12) |
The ratio
 |
(5.13) |
is known as the square of the multiple correlation between  and the
and the 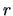 variables
variables  . It is the percentage of the variance of
. It is the percentage of the variance of  which is
explained by the linear approximation
which is
explained by the linear approximation
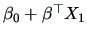 . The last
term in (5.12) is the residual variance of
. The last
term in (5.12) is the residual variance of  . The square of the
multiple correlation corresponds to the coefficient of determination
introduced in Section 3.4, see (3.39), but here it is defined
in terms of the r.v.
. The square of the
multiple correlation corresponds to the coefficient of determination
introduced in Section 3.4, see (3.39), but here it is defined
in terms of the r.v.  and
and  . It can be shown that
. It can be shown that
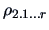 is also the
maximum correlation attainable between
is also the
maximum correlation attainable between  and a linear combination of the
elements of
and a linear combination of the
elements of  , the optimal linear combination being precisely given by
, the optimal linear combination being precisely given by
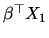 . Note, that when
. Note, that when  , the multiple
correlation
, the multiple
correlation 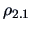 coincides with the usual simple correlation
coincides with the usual simple correlation
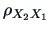 between
between  and
and  .
.
EXAMPLE 5.3
Consider the ``classic blue'' pullover example (Example
3.15) and suppose
that

(sales),

(price),
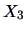
(advertisement) and
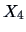
(sales
assistants) are normally distributed with
(These are in fact the sample mean and the sample covariance matrix but in this
example we pretend that they are the true parameter values.)
The conditional distribution of  given
given
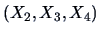 is thus an
univariate normal with mean
is thus an
univariate normal with mean
and variance
The linear approximation of the sales
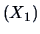
by the price
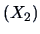
,
advertisement
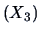
and sales assistants
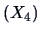
is provided by the
conditional mean above.(Note that this coincides with the results of Example
3.15 due to the particular choice of
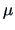
and
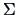
). The quality of the
approximation is given by the multiple correlation
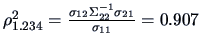
. (Note again that this coincides with the coefficient of determination
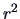
found in Example
3.15).
This example also illustrates the concept of partial
correlation. The correlation matrix between the 4 variables is given by
so that the correlation between

(sales) and

(price) is
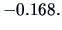
We can compute the conditional distribution of
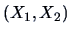
given
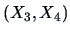
, which is a bivariate normal with mean:
and covariance matrix:
In particular, the last covariance matrix allows the partial
correlation between

and

to be computed
for a fixed level of
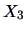
and
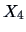
:
so that in this particular example with a fixed level of advertisement and sales
assistance, the negative correlation between price and sales is more important than the marginal one.
Summary

-
If
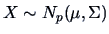 , then a linear transformation
, then a linear transformation
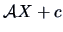 ,
,
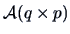 , where
, where
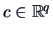 ,
has distribution
,
has distribution
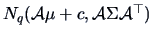 .
.

-
Two linear transformations
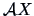 and
and 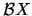 with
with
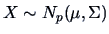 are independent if and only if
are independent if and only if
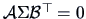 .
.

-
If
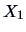 and
and 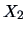 are partitions of
are partitions of
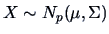 ,
then the conditional distribution of
,
then the conditional distribution of 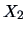 given
given 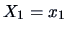 is
again normal.
is
again normal.

-
In the multivariate normal case,
 is independent of
is independent of  if and
only if
if and
only if 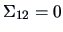 .
.

-
The conditional expectation of
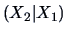 is a linear function if
is a linear function if
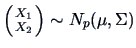 .
.

-
The multiple correlation coefficient is defined as
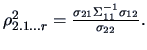

-
The multiple correlation coefficient is the percentage of the variance of
 explained by
the linear approximation
explained by
the linear approximation
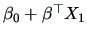 .
.
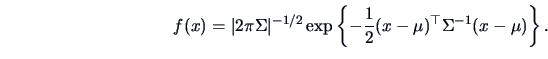
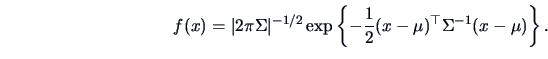
![]() into sub-vectors
into sub-vectors
![]() and
and ![]() . The following theorem tells us how to correct
. The following theorem tells us how to correct
![]() to obtain a vector which is independent of
to obtain a vector which is independent of ![]() .
.

![\begin{eqnarray*}
X_1&=&\data{A}X\quad \textrm{ with } \quad \data{A}=[\ \data{I...
...\data{B}=[\ -\Sigma_{21}
\Sigma_{11}^{-1}\ ,\ \data{I}_{p-r}\ ].
\end{eqnarray*}](mvahtmlimg1630.gif)
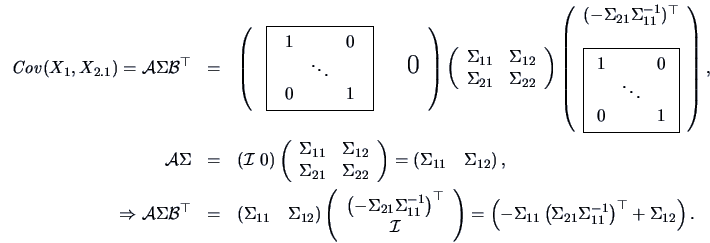
![]() ), namely
), namely
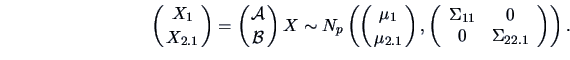
![]() ) can easily be factorized into
) can easily be factorized into
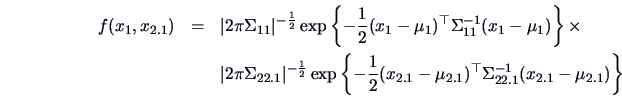
![]() can be
shown via the following corollary.
can be
shown via the following corollary.
![]() given
given ![]() is given by the next theorem.
is given by the next theorem.
![]() ,
for a fixed value of
,
for a fixed value of ![]() ,
, ![]() is equivalent to
is equivalent to ![]() plus
a constant term:
plus
a constant term:
![]() is a linear function of
is a linear function of
![]() and that the conditional variance does not depend on the particular
value of
and that the conditional variance does not depend on the particular
value of ![]() . In the following example we consider a specific distribution.
. In the following example we consider a specific distribution.
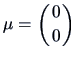 and
and
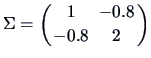 .
Then
.
Then
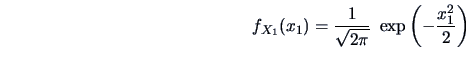
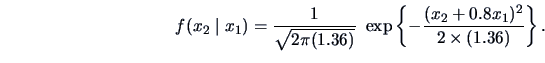
![]() and the conditional distribution
and the conditional distribution ![]() . The following theorem
shows under which conditions this can be easily done in the multinormal
framework.
. The following theorem
shows under which conditions this can be easily done in the multinormal
framework.
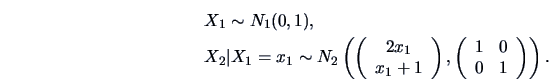
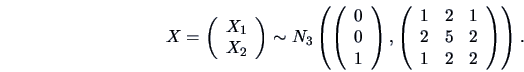
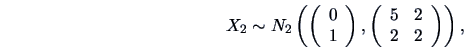
![]() could have
also been computed directly by using (4.28)-(4.29).
Using the derivation above, however, provides us with useful properties:
we have multinormality!
could have
also been computed directly by using (4.28)-(4.29).
Using the derivation above, however, provides us with useful properties:
we have multinormality!
![]() is the mean squared error (MSE) best
approximation of
is the mean squared error (MSE) best
approximation of ![]() by a function of
by a function of ![]() . We have in this case that
. We have in this case that
![]() . Now
. Now
![]() and
and
![]() is a row vector
is a row vector ![]() of dimension
of dimension ![]()

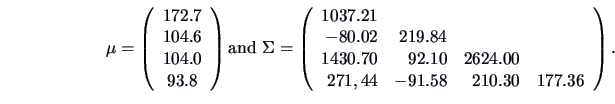
![]() given
given
![]() is thus an
univariate normal with mean
is thus an
univariate normal with mean
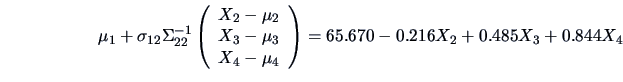
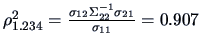 . (Note again that this coincides with the coefficient of determination
. (Note again that this coincides with the coefficient of determination