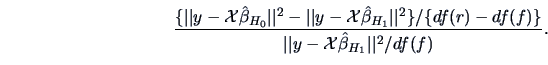3.6 Multiple Linear Model
The simple linear model and the analysis of variance model
can be viewed as a particular case of a more general linear model where
the variations of one variable 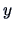 are explained by
are explained by 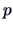 explanatory variables
explanatory variables 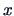 respectively.
Let
respectively.
Let
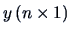 and
and
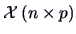 be a vector of observations on the response variable and a data matrix on
the
be a vector of observations on the response variable and a data matrix on
the 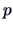 explanatory variables. An important application of the developed
theory is the least squares fitting. The idea is to
approximate
explanatory variables. An important application of the developed
theory is the least squares fitting. The idea is to
approximate 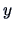 by a linear combination
by a linear combination 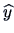 of columns of
of columns of 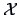 ,
i.e.,
,
i.e.,
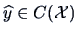 .
The problem is to find
.
The problem is to find
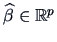 such that
such that
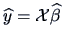 is the best fit of
is the best fit of 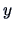 in the
least-squares sense. The linear model can be written as
in the
least-squares sense. The linear model can be written as
 |
(3.50) |
where  are the errors. The least squares solution is given by
are the errors. The least squares solution is given by
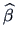 :
:
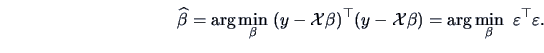 |
(3.51) |
Suppose that
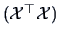 is of full rank and thus invertible.
Minimizing the expression (3.51) with respect to
is of full rank and thus invertible.
Minimizing the expression (3.51) with respect to 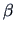 yields:
yields:
 |
(3.52) |
The fitted value
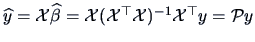 is the projection of
is the projection of 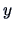 onto
onto 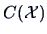 as
computed in (2.47).
as
computed in (2.47).
The least squares residuals are
The vector 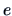 is the projection
of
is the projection
of 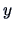 onto the orthogonal complement of
onto the orthogonal complement of 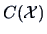 .
.
REMARK 3.5
A linear model with an intercept
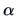
can also be written in this framework.
The approximating equation is:
This can be written as:
where
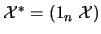
(we add a column of ones to the data).
We have by (
3.52):
EXAMPLE 3.15
Let us come back to the ``classic blue'' pullovers example. In Example
3.11, we considered the regression fit of the sales
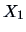
on the price
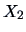
and concluded that there was only a small
influence of sales by changing the prices. A linear model
incorporating all three variables
allows us to approximate sales as a linear
function of price (
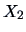
), advertisement
(
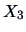
) and presence of sales assistants (
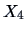
) simultaneously.
Adding a column of ones to the data (in order to estimate
the intercept
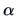
) leads to
The coefficient of determination is computed as before in (
3.40) and is:
We conclude that the variation of
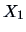
is well
approximated by the linear relation.
REMARK 3.6
The coefficient of determination
is
influenced by the number of regressors. For a given sample size
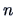
, the
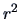
value will increase by adding more regressors into the linear model. The value
of
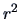
may therefore be high even if possibly
irrelevant regressors are included. A
corrected coefficient of determination
for
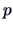
regressors and a constant intercept (
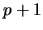
parameters) is
 |
(3.53) |
EXAMPLE 3.16
The corrected coefficient of determination for Example
3.15
is
This means that
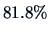
of the variation of the response variable
is explained by the explanatory variables.
Note that the linear model (3.50) is very flexible and
can model nonlinear relationships between the response 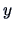 and the
explanatory variables
and the
explanatory variables 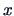 . For example, a quadratic relation in one
variable
. For example, a quadratic relation in one
variable 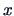 could be included.
Then
could be included.
Then
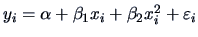 could be written in matrix notation as in (3.50),
could be written in matrix notation as in (3.50),
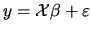 where
where
When 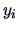 is the
is the 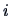 -th observation of a random variable
-th observation of a random variable 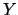 ,
the errors are also random. Under standard assumptions
(independence, zero mean and constant variance
,
the errors are also random. Under standard assumptions
(independence, zero mean and constant variance 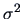 ),
inference can be conducted on
),
inference can be conducted on 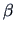 . Using the properties of
Chapter 4, it is easy to prove:
. Using the properties of
Chapter 4, it is easy to prove:
The analogue of the 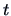 -test for the multivariate linear regression situation is
-test for the multivariate linear regression situation is
The standard error of each coefficient
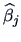 is
given by the square root of the diagonal elements of the matrix
is
given by the square root of the diagonal elements of the matrix
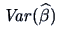 .
In standard situations, the variance
.
In standard situations, the variance 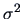 of the error
of the error  is not known. One may estimate it by
is not known. One may estimate it by
where 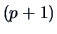 is the dimension of
is the dimension of 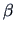 . In testing
. In testing 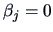 we reject the hypothesis at the significance level
we reject the hypothesis at the significance level 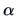 if
if
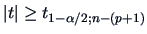 . More general issues on testing linear
models are addressed in Chapter 7.
. More general issues on testing linear
models are addressed in Chapter 7.
The simple ANOVA problem (Section 3.5)
may also be rewritten in matrix terms.
Recall the definition of a vector of ones from (2.1) and
define a vector of zeros as 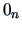 .
Then construct the following (
.
Then construct the following (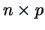 ) matrix, (here
) matrix, (here 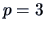 ),
),
 |
(3.54) |
where  . Equation (3.41) then reads as follows.
. Equation (3.41) then reads as follows.
The parameter vector is
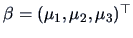 . The data
set from Example 3.14 can therefore be written as a linear
model
. The data
set from Example 3.14 can therefore be written as a linear
model
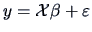 where
where
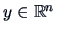 with
with
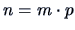 is the stacked vector of the columns of Table
3.1. The projection into the column space
is the stacked vector of the columns of Table
3.1. The projection into the column space 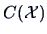 of
(3.54) yields the least-squares estimator
of
(3.54) yields the least-squares estimator
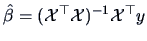 .
Note that
.
Note that
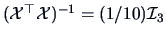 and that
and that
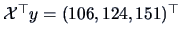 is the sum
is the sum
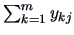 for each factor, i.e., the 3 column sums of Table 3.1.
The least squares estimator is therefore the
vector
for each factor, i.e., the 3 column sums of Table 3.1.
The least squares estimator is therefore the
vector
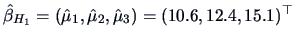 of sample means for each factor level
of sample means for each factor level
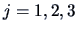 .
Under the null hypothesis of equal mean values
.
Under the null hypothesis of equal mean values
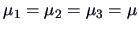 ,
we estimate the parameters under the same constraints.
This can be put into the form of a linear constraint:
,
we estimate the parameters under the same constraints.
This can be put into the form of a linear constraint:
This can be written as
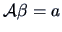 , where
, where
and
The constrained
least-squares solution can be shown (Exercise 3.24) to be given by:
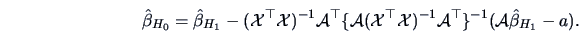 |
(3.55) |
It turns out that (3.55) amounts to simply calculating
the overall mean 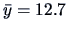 of the response
variable
of the response
variable 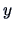 :
:
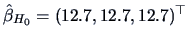 .
.
The F-test that has already been applied in
Example 3.14 can be written as
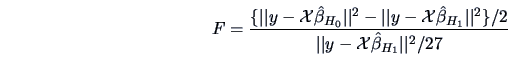 |
(3.56) |
which gives the same significant value 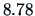 . Note that again we compare
the
. Note that again we compare
the 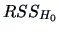 of the reduced model to the
of the reduced model to the 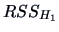 of the
full model. It corresponds to comparing the lengths of projections
into different column spaces.
This general approach in testing linear models is
described in detail in Chapter 7.
of the
full model. It corresponds to comparing the lengths of projections
into different column spaces.
This general approach in testing linear models is
described in detail in Chapter 7.
Summary

-
The relation
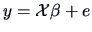 models a linear relation
between a one-dimensional variable
models a linear relation
between a one-dimensional variable 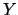 and a
and a 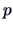 -dimensional
variable
-dimensional
variable 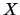 .
.
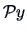 gives the best linear regression fit of the vector
gives the best linear regression fit of the vector 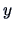 onto
onto
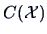 . The least squares parameter estimator is
. The least squares parameter estimator is
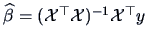 .
.

-
The simple ANOVA model can be written as a linear model.

-
The ANOVA model can be tested by comparing the length of the projection
vectors.

-
The test statistic of the F-Test can be written as

-
The adjusted coefficient of determination is
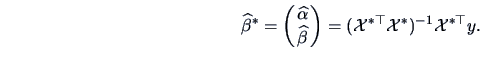

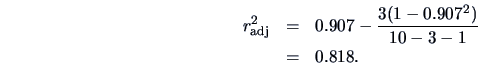
![]() and the
explanatory variables
and the
explanatory variables ![]() . For example, a quadratic relation in one
variable
. For example, a quadratic relation in one
variable ![]() could be included.
Then
could be included.
Then
![]() could be written in matrix notation as in (3.50),
could be written in matrix notation as in (3.50),
![]() where
where

![]() is the
is the ![]() -th observation of a random variable
-th observation of a random variable ![]() ,
the errors are also random. Under standard assumptions
(independence, zero mean and constant variance
,
the errors are also random. Under standard assumptions
(independence, zero mean and constant variance ![]() ),
inference can be conducted on
),
inference can be conducted on ![]() . Using the properties of
Chapter 4, it is easy to prove:
. Using the properties of
Chapter 4, it is easy to prove:

![]() -test for the multivariate linear regression situation is
-test for the multivariate linear regression situation is

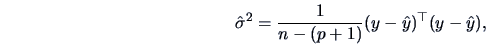
![]() .
Then construct the following (
.
Then construct the following (![]() ) matrix, (here
) matrix, (here ![]() ),
),
![]() . The data
set from Example 3.14 can therefore be written as a linear
model
. The data
set from Example 3.14 can therefore be written as a linear
model
![]() where
where
![]() with
with
![]() is the stacked vector of the columns of Table
3.1. The projection into the column space
is the stacked vector of the columns of Table
3.1. The projection into the column space ![]() of
(3.54) yields the least-squares estimator
of
(3.54) yields the least-squares estimator
![]() .
Note that
.
Note that
![]() and that
and that
![]() is the sum
is the sum
![]() for each factor, i.e., the 3 column sums of Table 3.1.
The least squares estimator is therefore the
vector
for each factor, i.e., the 3 column sums of Table 3.1.
The least squares estimator is therefore the
vector
![]() of sample means for each factor level
of sample means for each factor level
![]() .
Under the null hypothesis of equal mean values
.
Under the null hypothesis of equal mean values
![]() ,
we estimate the parameters under the same constraints.
This can be put into the form of a linear constraint:
,
we estimate the parameters under the same constraints.
This can be put into the form of a linear constraint:



![]() of the response
variable
of the response
variable ![]() :
:
![]() .
.