Let
![]() . A distance
. A distance ![]() is defined as a function
is defined as a function
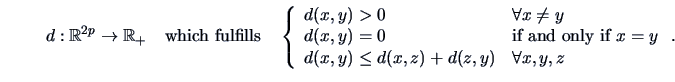
A Euclidean distance
![]() between two points
between two points ![]() and
and ![]() is defined as
is defined as
Note that the sets
![]() ,
i.e., the spheres with radius
,
i.e., the spheres with radius ![]() and
center
and
center ![]() , are the Euclidean
, are the Euclidean ![]() iso-distance
curves from the point
iso-distance
curves from the point ![]() (see Figure 2.2).
(see Figure 2.2).
The more general distance (2.32) with a positive definite matrix
![]() leads to the iso-distance curves
leads to the iso-distance curves
Let
![]() be the orthonormal eigenvectors of
be the orthonormal eigenvectors of
![]() corresponding to the eigenvalues
corresponding to the eigenvalues
![]() .
The resulting observations are given in the next theorem.
.
The resulting observations are given in the next theorem.
It is easy to find the coordinates of the tangency points between the
ellipsoid and its surrounding rectangle parallel to the coordinate
axes. Let us find the coordinates of the tangency point that are in the
direction of the ![]() -th coordinate axis (positive direction).
-th coordinate axis (positive direction).
For ease of notation, we suppose the ellipsoid is centered around the
origin ![]() . If not, the rectangle will be shifted by the value
of
. If not, the rectangle will be shifted by the value
of
![]() .
.
The coordinate of the tangency point is given by the solution to the
following problem:
 |
(2.35) |
The solution is computed via the Lagrangian
![]() which
by (2.23) leads to the following system of
equations:
which
by (2.23) leads to the following system of
equations:
Premultiplying (2.36) by ![]() , we
have from (2.37):
, we
have from (2.37):
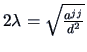 . We choose
the positive value of the square root because we are maximizing
. We choose
the positive value of the square root because we are maximizing
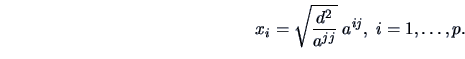 |
(2.39) |
The particular case where ![]() provides statement
provides statement ![]() in
Theorem 2.7.
in
Theorem 2.7.
Theorem 2.7 will prove to be particularly useful in many subsequent chapters. First, it provides a helpful tool for graphing an ellipse in two dimensions. Indeed, knowing the slope of the principal axes of the ellipse, their half-lengths and drawing the rectangle inscribing the ellipse allows one to quickly draw a rough picture of the shape of the ellipse.
In Chapter 7,
it is shown that the confidence region for the vector ![]() of a
multivariate normal population is given by a particular ellipsoid whose
parameters depend on sample characteristics. The rectangle inscribing the
ellipsoid (which is much easier to obtain) will provide the simultaneous
confidence intervals for all of the components in
of a
multivariate normal population is given by a particular ellipsoid whose
parameters depend on sample characteristics. The rectangle inscribing the
ellipsoid (which is much easier to obtain) will provide the simultaneous
confidence intervals for all of the components in ![]() .
.
In addition it will be shown that the contour surfaces of the
multivariate normal density are provided by ellipsoids whose parameters
depend on the mean vector and on the covariance matrix.
We will see that the tangency points between the contour
ellipsoids and the surrounding rectangle are determined by
regressing one component on the
![]() other components. For instance,
in the direction of the
other components. For instance,
in the direction of the ![]() -th axis, the tangency points are given by the
intersections of the ellipsoid contours with the regression line of the vector
of
-th axis, the tangency points are given by the
intersections of the ellipsoid contours with the regression line of the vector
of ![]() variables (all components except the
variables (all components except the ![]() -th) on the
-th) on the ![]() -th component.
-th component.
Consider a vector
![]() . The norm or length of
. The norm or length of ![]() (with respect to
the metric
(with respect to
the metric ![]() ) is defined as
) is defined as
Consider two vectors ![]() and
and
![]() . The angle
. The angle ![]() between
between ![]() and
and ![]() is defined by the cosine of
is defined by the cosine of ![]() :
:
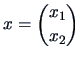 and
and
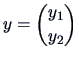 ,
we have
,
we have
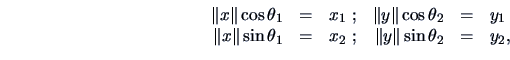 |
(2.41) |
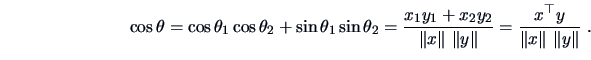
The angle can also be defined with respect to a general metric
![]()
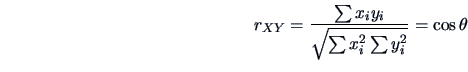
When we consider a point
![]() , we generally use a
, we generally use a ![]() -coordinate
system to obtain its geometric representation, like in Figure 2.1
for instance. There will be situations in multivariate techniques where we
will want to rotate this system of coordinates by the angle
-coordinate
system to obtain its geometric representation, like in Figure 2.1
for instance. There will be situations in multivariate techniques where we
will want to rotate this system of coordinates by the angle ![]() .
.
Consider for example the point ![]() with coordinates
with coordinates
![]() in
in
![]() with respect to a given set of orthogonal axes. Let
with respect to a given set of orthogonal axes. Let ![]() be a
be a
![]() orthogonal matrix where
orthogonal matrix where
 |
(2.44) |
| (2.45) |
| (2.46) |
More generally, premultiplying a vector ![]() by an orthogonal matrix
by an orthogonal matrix ![]() geometrically corresponds to a rotation of the system of axes, so that the
first new axis is determined by the first row of
geometrically corresponds to a rotation of the system of axes, so that the
first new axis is determined by the first row of ![]() .
This geometric point of view will be exploited in
Chapters 9 and 10.
.
This geometric point of view will be exploited in
Chapters 9 and 10.
Define for
![]()
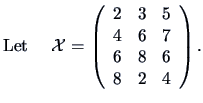 It is easy to show (e.g. by calculating the determinant of
It is easy to show (e.g. by calculating the determinant of
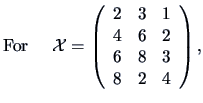 the third column is a multiple of the first one and the matrix
the third column is a multiple of the first one and the matrix ![]() cannot be of full rank. Noticing that the first two columns of
cannot be of full rank. Noticing that the first two columns of ![]() are independent, we see that
are independent, we see that
![]() .
In this case, the dimension of the columns space is 2 and the dimension of the
null space is 1.
.
In this case, the dimension of the columns space is 2 and the dimension of the
null space is 1.
A matrix
![]() is called an (orthogonal) projection
matrix in
is called an (orthogonal) projection
matrix in ![]() if
and only if
if
and only if
![]() (
(![]() is idempotent).
Let
is idempotent).
Let
![]() . Then
. Then ![]() is the projection of
is the projection of ![]() on
on
![]() .
.
Consider
![]() and let
and let
| (2.48) |
PROOF:
(i) holds, since
![]() ,
where
,
where
![]() .
.
(ii) follows from
![]() and
and
![]() .
.
![]()
