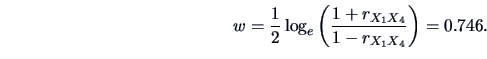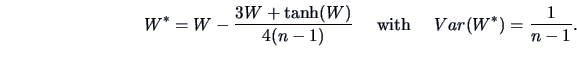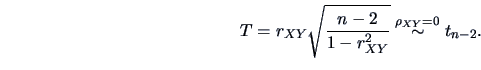3.2 Correlation
The correlation between two variables  and
and 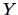 is defined from the covariance as the following:
is defined from the covariance as the following:
 |
(3.7) |
The advantage of the correlation is that it is independent of the scale, i.e.,
changing the variables' scale of measurement does not change the
value of the correlation. Therefore, the correlation is more useful as a
measure of association between two random variables than the covariance.
The empirical version of 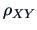 is as follows:
is as follows:
 |
(3.8) |
The correlation is in absolute value always less than 1. It is zero
if the covariance is zero and vice-versa.
For  -dimensional vectors
-dimensional vectors
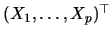 we have the
theoretical correlation matrix
we have the
theoretical correlation matrix
and its empirical version, the empirical correlation matrix which can
be calculated from the observations,
EXAMPLE 3.3
We obtain the following correlation matrix for the genuine bank notes:
 |
(3.9) |
and for the counterfeit bank notes:
 |
(3.10) |
As noted before for
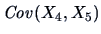
, the correlation between
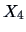
(distance of the frame to the lower border)
and
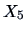
(distance of the frame to the upper border)
is negative. This is natural, since the covariance and correlation always
have the same sign (see also Exercise
3.17).
Why is the correlation an interesting statistic to study?
It is related to independence of random variables, which we shall
define more formally later on. For the moment we may think of
independence as the fact that one variable has no influence on
another.
1mm
![\begin{picture}(2.00,2.00)
\par\linethickness{1.0pt}\put(0.00,0.00){\line(1,0){1...
...\line(1,-2){5.00}}
\put(5.00,4.00){\makebox(0,0)[cc]{\LARGE\bf !}}
\end{picture}](mvahtmlimg711.gif)
In general, the converse is not true, as the following example
shows.
EXAMPLE 3.4
Consider a standard normally-distributed random variable

and a
random variable
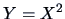
, which is surely not independent of

. Here we have
(because
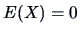
and
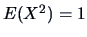
). Therefore
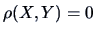
, as well.
This example also shows that correlations and covariances measure only
linear dependence. The quadratic dependence of
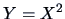
on

is not
reflected by these measures of dependence.
REMARK 3.1
For two normal random variables,
the converse of Theorem
3.1 is true:
zero covariance for two normally-distributed random variables
implies independence. This will be shown later in Corollary
5.2.
Theorem 3.1 enables us to check for independence
between the components of a bivariate normal random variable.
That is, we can use the correlation and test whether it is zero.
The distribution of  for an
arbitrary
for an
arbitrary  is unfortunately complicated.
The distribution of
is unfortunately complicated.
The distribution of 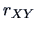 will be more accessible if
will be more accessible if 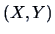 are jointly normal (see Chapter 5).
If we transform the correlation by Fisher's
are jointly normal (see Chapter 5).
If we transform the correlation by Fisher's  -transformation,
-transformation,
 |
(3.11) |
we obtain a variable that has a more accessible distribution.
Under the hypothesis that 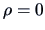 ,
, 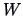 has an asymptotic normal
distribution.
Approximations of the expectation and variance of
has an asymptotic normal
distribution.
Approximations of the expectation and variance of 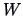 are given by the following:
are given by the following:
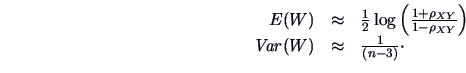 |
(3.12) |
The distribution is given in Theorem 3.2.
The symbol ``
 '' denotes convergence in
distribution, which will be explained in more detail in Chapter 4.
'' denotes convergence in
distribution, which will be explained in more detail in Chapter 4.
Theorem 3.2 allows us to test different hypotheses on correlation.
We can fix the level of significance 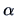 (the probability of rejecting
a true hypothesis) and reject the hypothesis if the difference
between the hypothetical value and the calculated value of
(the probability of rejecting
a true hypothesis) and reject the hypothesis if the difference
between the hypothetical value and the calculated value of 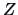 is
greater than the corresponding critical value of the normal distribution.
The following example illustrates the procedure.
is
greater than the corresponding critical value of the normal distribution.
The following example illustrates the procedure.
EXAMPLE 3.5
Let's study the correlation between mileage (

) and weight
(
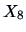
) for the car data set (
B.3) where
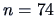
.
We have
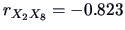
. Our conclusions from
the boxplot in Figure
1.3 (``Japanese cars
generally have better mileage than the others'') needs to be revised.
From Figure
3.3 and
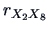
, we can see that
mileage is highly correlated with weight, and that the Japanese cars
in the sample are in fact all lighter than the others!
If we want to know whether
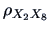 is significantly different
from
is significantly different
from 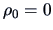 , we apply Fisher's
, we apply Fisher's 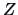 -transform (3.11).
This gives us
-transform (3.11).
This gives us
i.e., a highly significant value to reject the hypothesis that
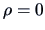
(the 2.5% and 97.5% quantiles of the normal distribution are
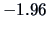
and
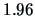
, respectively).
If we want to test the hypothesis that, say,
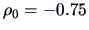
, we obtain:
This is a nonsignificant value at the
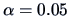
level for
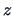
since
it is between the critical values
at the 5% significance level (i.e.,
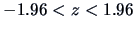
).
Figure 3.3:
Mileage (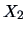 ) vs. weight (
) vs. weight (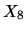 ) of U.S. (star),
European (plus signs) and Japanese (circle) cars.
) of U.S. (star),
European (plus signs) and Japanese (circle) cars.
 MVAscacar.xpl
MVAscacar.xpl
|
|
EXAMPLE 3.6
Let us consider again the pullovers data set from example
3.2.
Consider the correlation between the presence of the sales
assistants (
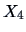
) vs. the number of sold pullovers (
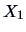
)
(see Figure
3.4). Here we compute the correlation as
Figure 3.4:
Hours of sales assistants (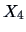 )
vs. sales (
)
vs. sales ( ) of pullovers.
) of pullovers.
 MVAscapull2.xpl
MVAscapull2.xpl
|
|
The 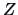 -transform of this value is
-transform of this value is
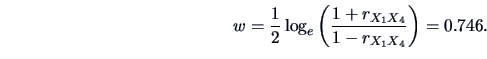 |
(3.14) |
The sample size is
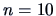
, so for the hypothesis
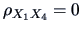
,
the statistic to consider is:
 |
(3.15) |
which is just statistically significant at the
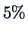
level (i.e., 1.974 is just a little larger than 1.96).
REMARK 3.2
The normalizing and variance stabilizing properties of
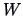
are asymptotic.
In addition the use of
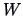
in small samples (for
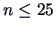
) is improved by
Hotelling's transform (
Hotelling; 1953):
The transformed variable
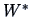
is asymptotically distributed as a normal distribution.
EXAMPLE 3.7
From the preceding remark, we obtain
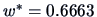
and
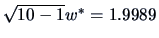
for the preceding Example
3.6. This value is significant
at the
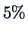
level.
REMARK 3.3
Note that the Fisher's Z-transform is the inverse
of the hyperbolic tangent function:
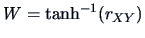
; equivalently
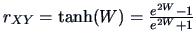
.
REMARK 3.4
Under the assumptions of normality of

and
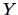
, we may
test their independence (
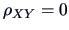
) using the exact
-distribution of
the statistic
Setting the probability of the first error type to
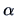
,
we reject the null hypothesis
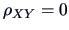
if
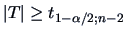
.
Summary

- The correlation is a standardized measure of dependence.

- The absolute value of the correlation is always less
than one.

- Correlation measures only linear dependence.

- There are nonlinear dependencies that have zero
correlation.

- Zero correlation does not imply independence.

- Independence implies zero correlation.

-
Negative correlation corresponds to downward-sloping
scatterplots.

- Positive correlation corresponds to upward-sloping
scatterplots.

- Fisher's Z-transform helps us in testing hypotheses on
correlation.

- For small samples, Fisher's Z-transform can be improved by
the transformation
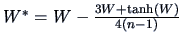 .
.

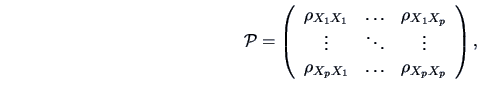

![]()
![]() for an
arbitrary
for an
arbitrary ![]() is unfortunately complicated.
The distribution of
is unfortunately complicated.
The distribution of ![]() will be more accessible if
will be more accessible if ![]() are jointly normal (see Chapter 5).
If we transform the correlation by Fisher's
are jointly normal (see Chapter 5).
If we transform the correlation by Fisher's ![]() -transformation,
-transformation,
![]() '' denotes convergence in
distribution, which will be explained in more detail in Chapter 4.
'' denotes convergence in
distribution, which will be explained in more detail in Chapter 4.
![]() (the probability of rejecting
a true hypothesis) and reject the hypothesis if the difference
between the hypothetical value and the calculated value of
(the probability of rejecting
a true hypothesis) and reject the hypothesis if the difference
between the hypothetical value and the calculated value of ![]() is
greater than the corresponding critical value of the normal distribution.
The following example illustrates the procedure.
is
greater than the corresponding critical value of the normal distribution.
The following example illustrates the procedure.
![]() is significantly different
from
is significantly different
from ![]() , we apply Fisher's
, we apply Fisher's ![]() -transform (3.11).
This gives us
-transform (3.11).
This gives us
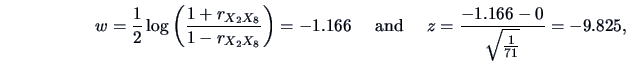
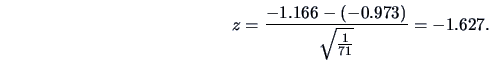
![\includegraphics[width=1\defpicwidth]{scacar.ps}](mvahtmlimg739.gif)
![]() -transform of this value is
-transform of this value is