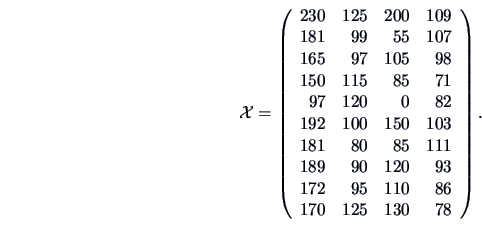3.1 Covariance
Covariance is a measure of dependency between random variables.
Given two (random) variables 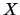 and
and 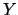 the (theoretical) covariance
is defined by:
the (theoretical) covariance
is defined by:
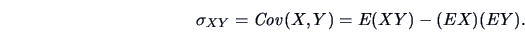 |
(3.1) |
The precise definition of expected values is given in Chapter 4.
If 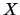 and
and 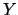 are independent
of each other, the covariance
are independent
of each other, the covariance
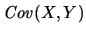 is necessarily equal to zero, see Theorem 3.1.
The converse is not true.
The covariance of
is necessarily equal to zero, see Theorem 3.1.
The converse is not true.
The covariance of 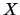 with itself is the variance:
with itself is the variance:
If the variable 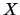 is
is 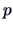 -dimensional multivariate, e.g.,
-dimensional multivariate, e.g.,
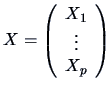 , then the
theoretical covariances among all the elements are put into matrix form,
i.e., the covariance matrix:
, then the
theoretical covariances among all the elements are put into matrix form,
i.e., the covariance matrix:
Properties of covariance matrices will be detailed in Chapter 4.
Empirical versions of these quantities are:
For small 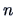 , say
, say 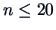 , we should replace the factor
, we should replace the factor 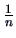 in (3.2) and (3.3)
by
in (3.2) and (3.3)
by 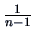 in order to correct for a small bias.
For a
in order to correct for a small bias.
For a 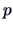 -dimensional random variable, one obtains the empirical
covariance matrix (see Section 3.3 for properties and details)
-dimensional random variable, one obtains the empirical
covariance matrix (see Section 3.3 for properties and details)
For a scatterplot of two variables the covariances measure ``how close
the scatter is to a line''. Mathematical details follow but it should
already be understood here that in this sense covariance measures only
``linear dependence''.
EXAMPLE 3.1
If
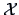
is the entire bank data set, one obtains the covariance
matrix
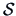
as indicated below:
 |
(3.4) |
The empirical covariance between
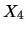
and
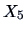
, i.e.,
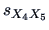
,
is found in row 4 and column 5. The value is
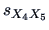
= 0.16.
Is it obvious that this value is positive? In Exercise
3.1 we will
discuss this question further.
If 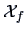 denotes the counterfeit bank notes, we obtain:
denotes the counterfeit bank notes, we obtain:
 |
(3.5) |
For the genuine,
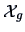
, we have:
 |
(3.6) |
Note that the covariance between 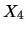 (distance of the frame to the lower
border) and
(distance of the frame to the lower
border) and 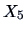 (distance of the frame to the upper border) is negative in
both (3.5) and (3.6)! Why would this happen?
In Exercise 3.2 we will discuss this question in more detail.
(distance of the frame to the upper border) is negative in
both (3.5) and (3.6)! Why would this happen?
In Exercise 3.2 we will discuss this question in more detail.
At first sight, the matrices
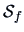 and
and
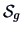 look different, but they create
almost the same scatterplots (see the discussion in Section 1.4).
Similarly, the common principal component analysis in
Chapter 9 suggests a joint analysis of the covariance structure
as in Flury and Riedwyl (1988).
look different, but they create
almost the same scatterplots (see the discussion in Section 1.4).
Similarly, the common principal component analysis in
Chapter 9 suggests a joint analysis of the covariance structure
as in Flury and Riedwyl (1988).
Figure 3.1:
Scatterplot of variables 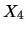 vs.
vs. 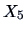 of the entire bank data set.
of the entire bank data set.
 MVAscabank45.xpl
MVAscabank45.xpl
|
|
Scatterplots with point clouds that are ``upward-sloping'', like the one
in the upper left of Figure 1.14, show variables with positive
covariance.
Scatterplots with ``downward-sloping'' structure have negative covariance.
In Figure 3.1 we show the scatterplot of
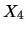 vs.
vs. 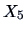 of the entire bank data set.
The point cloud is upward-sloping. However, the two sub-clouds of
counterfeit and genuine bank notes are downward-sloping.
of the entire bank data set.
The point cloud is upward-sloping. However, the two sub-clouds of
counterfeit and genuine bank notes are downward-sloping.
EXAMPLE 3.2
A textile shop manager is studying the sales of ``classic blue''
pullovers
over 10 different periods.
He observes the number of pullovers sold
(
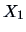
), variation in price (
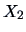
, in EUR), the advertisement
costs in local newspapers (
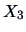
, in EUR) and the presence of a sales
assistant (
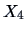
, in hours per period). Over the periods, he observes
the following data matrix:
He is convinced that the price must have a large influence on the
number of pullovers sold. So he makes a scatterplot of
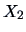
vs.
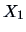
, see Figure
3.2.
Figure 3.2:
Scatterplot of variables 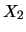 vs.
vs. 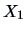 of the
pullovers data set.
of the
pullovers data set.
 MVAscapull1.xpl
MVAscapull1.xpl
|
|
A rough impression is that the cloud is somewhat downward-sloping. A
computation of the empirical covariance yields
a negative value as expected.
Note: The covariance function is scale dependent. Thus, if the prices in this example were in Japanese Yen (JPY), we would obtain
a different answer (see Exercise 3.16).
A measure of (linear) dependence independent of the scale is the correlation,
which we introduce in the next section.
Summary

- The covariance is a measure of dependence.

- Covariance measures only linear dependence.

- Covariance is scale dependent.

- There are nonlinear dependencies that have zero
covariance.

- Zero covariance does not imply independence.

- Independence implies zero covariance.

-
Negative covariance corresponds to downward-sloping
scatterplots.

- Positive covariance corresponds to upward-sloping
scatterplots.

- The covariance of a variable with itself is its variance
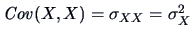 .
.

- For small
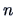 , we should replace the factor
, we should replace the factor 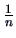 in the
computation of the covariance by
in the
computation of the covariance by 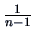 .
.
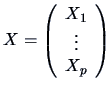 , then the
theoretical covariances among all the elements are put into matrix form,
i.e., the covariance matrix:
, then the
theoretical covariances among all the elements are put into matrix form,
i.e., the covariance matrix:
![]() denotes the counterfeit bank notes, we obtain:
denotes the counterfeit bank notes, we obtain:
![]() (distance of the frame to the lower
border) and
(distance of the frame to the lower
border) and ![]() (distance of the frame to the upper border) is negative in
both (3.5) and (3.6)! Why would this happen?
In Exercise 3.2 we will discuss this question in more detail.
(distance of the frame to the upper border) is negative in
both (3.5) and (3.6)! Why would this happen?
In Exercise 3.2 we will discuss this question in more detail.
![]() and
and
![]() look different, but they create
almost the same scatterplots (see the discussion in Section 1.4).
Similarly, the common principal component analysis in
Chapter 9 suggests a joint analysis of the covariance structure
as in Flury and Riedwyl (1988).
look different, but they create
almost the same scatterplots (see the discussion in Section 1.4).
Similarly, the common principal component analysis in
Chapter 9 suggests a joint analysis of the covariance structure
as in Flury and Riedwyl (1988).
![]() vs.
vs. ![]() of the entire bank data set.
The point cloud is upward-sloping. However, the two sub-clouds of
counterfeit and genuine bank notes are downward-sloping.
of the entire bank data set.
The point cloud is upward-sloping. However, the two sub-clouds of
counterfeit and genuine bank notes are downward-sloping.