Suppose that
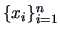 is an i.i.d. sample from a population
with pdf
is an i.i.d. sample from a population
with pdf 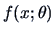 . The aim is to estimate
. The aim is to estimate
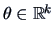 which
is a vector of unknown parameters.
The likelihood function is defined as the
joint density
which
is a vector of unknown parameters.
The likelihood function is defined as the
joint density
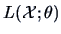 of the observations
of the observations 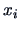 considered as a function
of
considered as a function
of 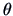 :
:
 |
(6.1) |
where 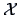 denotes the sample of the data matrix with the observations
denotes the sample of the data matrix with the observations
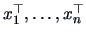 in each row.
The maximum likelihood estimator (MLE) of
in each row.
The maximum likelihood estimator (MLE) of 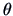 is defined as
is defined as
Often it is easier to maximize the log-likelihood
function
 |
(6.2) |
which is equivalent since the logarithm is a monotone one-to-one
function. Hence
The following examples illustrate cases where the maximization process can be
performed analytically, i.e., we will obtain an explicit analytical
expression for
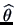 . Unfortunately, in other situations, the
maximization process can be more intricate, involving nonlinear optimization
techniques. In the latter case, given a sample
. Unfortunately, in other situations, the
maximization process can be more intricate, involving nonlinear optimization
techniques. In the latter case, given a sample 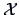 and the likelihood
function, numerical methods will be used to determine the value of
and the likelihood
function, numerical methods will be used to determine the value of 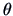 maximizing
maximizing
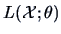 or
or
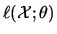 . These numerical methods
are typically based on Newton-Raphson iterative techniques.
. These numerical methods
are typically based on Newton-Raphson iterative techniques.
EXAMPLE 6.1
Consider a sample
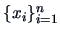
from
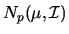
,
i.e., from the pdf
where
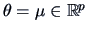
is the mean vector parameter. The log-likelihood
is in this case
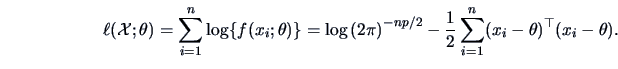 |
(6.3) |
The term
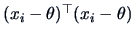
equals
Summing this term over
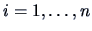
we see that
Hence
Only the last term depends on
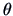
and is obviously maximized for
Thus
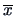
is the MLE of
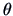
for this family of
pdfs
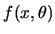
.
A more complex example is the following one where we derive
the MLE's for 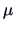 and
and 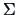 .
.
EXAMPLE 6.2
Suppose
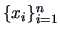
is a sample from a normal
distribution
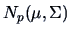
.
Here
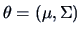
with
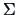
interpreted as a vector.
Due to the symmetry of
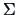
the unknown parameter
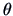
is in fact
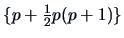
-dimensional. Then
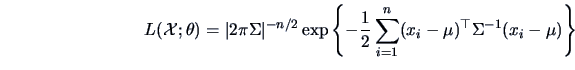 |
(6.4) |
and
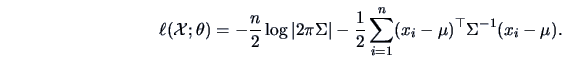 |
(6.5) |
The term
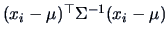 equals
equals
Summing this term over
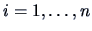
we see that
Note that from (
2.14)
Therefore, by summing over the index
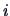
we finally arrive at
Thus the log-likelihood function for
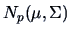
is
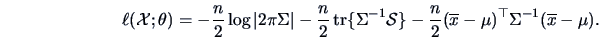 |
(6.6) |
We can easily see that the third term is maximized by
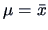
. In fact the MLE's are given by
The derivation of
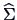
is a lot more complicated.
It involves derivatives with respect to matrices with their
notational complexities and will not be presented here:
for a more elaborate proof see
Mardia et al. (1979, p.103-104).
Note that the unbiased covariance estimator
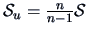
is not the MLE of
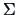
!
EXAMPLE 6.3
Consider the linear regression model
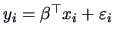
for
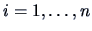
, where
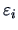
is i.i.d.
and
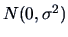
and where
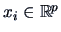
. Here
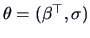
is a
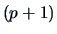
-dimensional parameter vector. Denote
Then
and
Differentiating w.r.t. the parameters yields
Note that
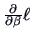
denotes the vector of
the derivatives w.r.t. all components of
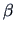
(the gradient).
Since the first equation only depends on
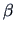
, we start with
deriving
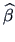
.
Plugging
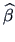
into the second equation gives
where
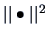
denotes the Euclidean vector norm from Section
2.6. We see that the MLE
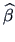
is
identical with the least squares estimator (
3.52). The variance
estimator
is nothing else than the residual sum of squares (RSS) from
(
3.37) generalized to the case of multivariate
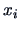
.
Note that when the 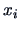 are considered
to be fixed we have
are considered
to be fixed we have
Then, using the properties of moments from Section
4.2 we have
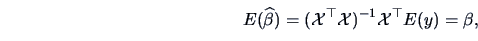 |
(6.7) |
 |
(6.8) |
Summary

-
If
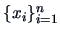 is an i.i.d. sample from a distribution with
pdf
is an i.i.d. sample from a distribution with
pdf 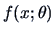 , then
, then
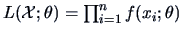 is the likelihood function.
The maximum likelihood estimator (MLE) is that value of
is the likelihood function.
The maximum likelihood estimator (MLE) is that value of 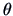 which maximizes
which maximizes
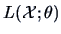 . Equivalently one can maximize the
log-likelihood
. Equivalently one can maximize the
log-likelihood
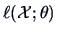 .
.

-
The MLE's of
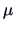 and
and 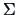 from a
from a
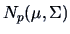 distribution are
distribution are
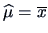 and
and
 . Note that the MLE of
. Note that the MLE of 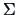 is not
unbiased.
is not
unbiased.

-
The MLE's of
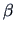 and
and 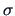 in the linear model
in the linear model
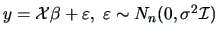 are given by the least squares estimator
are given by the least squares estimator
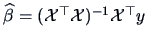 and
and
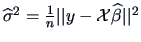 .
.
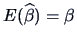 and
and
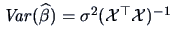 .
.
![]() is an i.i.d. sample from a population
with pdf
is an i.i.d. sample from a population
with pdf ![]() . The aim is to estimate
. The aim is to estimate
![]() which
is a vector of unknown parameters.
The likelihood function is defined as the
joint density
which
is a vector of unknown parameters.
The likelihood function is defined as the
joint density
![]() of the observations
of the observations ![]() considered as a function
of
considered as a function
of ![]() :
:


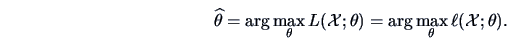
![]() . Unfortunately, in other situations, the
maximization process can be more intricate, involving nonlinear optimization
techniques. In the latter case, given a sample
. Unfortunately, in other situations, the
maximization process can be more intricate, involving nonlinear optimization
techniques. In the latter case, given a sample ![]() and the likelihood
function, numerical methods will be used to determine the value of
and the likelihood
function, numerical methods will be used to determine the value of ![]() maximizing
maximizing
![]() or
or
![]() . These numerical methods
are typically based on Newton-Raphson iterative techniques.
. These numerical methods
are typically based on Newton-Raphson iterative techniques.
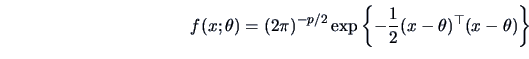
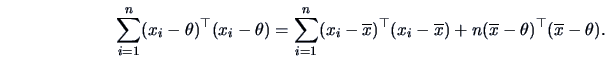
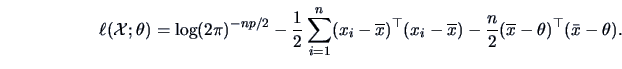
![]() and
and ![]() .
.
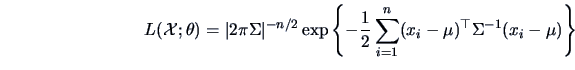
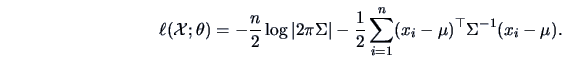
![]() equals
equals
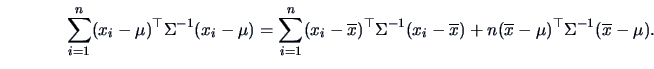
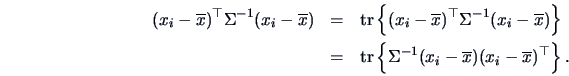
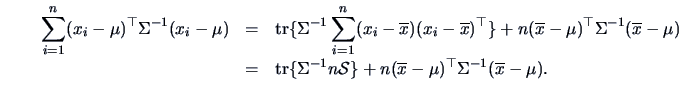
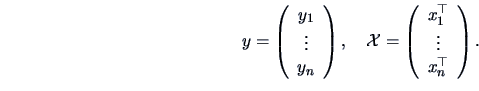
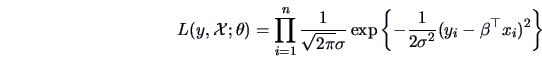
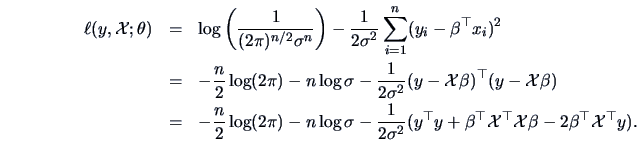
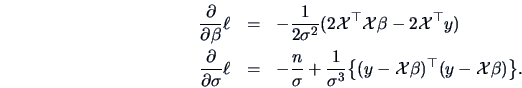
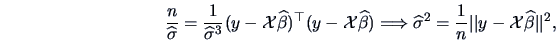

![]() are considered
to be fixed we have
are considered
to be fixed we have