9.1 Standardized Linear Combinations

The main objective of principal components analysis (PC) is to reduce the dimension of the observations. The simplest way of dimension reduction is to take just one element of the observed vector and to discard all others. This is not a very reasonable approach, as we have seen in the earlier chapters, since strength may be lost in interpreting the data. In the bank notes example we have seen that just one variable (e.g. $X_1$ = length) had no discriminatory power in distinguishing counterfeit from genuine bank notes. An alternative method is to weight all variables equally, i.e., to consider the simple average $p^{-1}\sum^p_{j=1}X_j$ of all the elements in the vector $X=(X_1,\ldots ,X_p)^{\top}$. This again is undesirable, since all of the elements of $X$ are considered with equal importance (weight).

A more flexible approach is to study a weighted average, namely

$$\delta ^{\top}X=\sum ^p_{j=1}\delta _jX_j\quad \ \textrm{so that}\quad \sum^p_{j=1} \delta ^2_j=1.$$ (9.1)

The weighting vector $\delta =(\delta _1,\ldots ,\delta _p)^{\top}$ can then be optimized to investigate and to detect specific features. We call (9.1) a standardized linear combination (SLC). Which SLC should we choose? One aim is to maximize the variance of the projection $\delta^{\top}X$, i.e., to choose $\delta$ according to

$$\max_{\{\delta :\Vert\delta \Vert=1\}}\mathop{\mathit{Var}}(... ..._{\{\delta :\Vert\delta \Vert=1\}}\delta^{\top}\Var(X)\delta.$$ (9.2)

The interesting ``directions" of $\delta$ are found through the spectral decomposition of the covariance matrix. Indeed, from Theorem 2.5, the direction $\delta$ is given by the eigenvector $\gamma_{1}$ corresponding to the largest eigenvalue $\lambda_{1}$ of the covariance matrix $\Sigma=\Var(X)$.

Figures 9.1 and 9.2 show two such projections (SLCs) of the same data set with zero mean. In Figure 9.1 an arbitrary projection is displayed. The upper window shows the data point cloud and the line onto which the data are projected. The middle window shows the projected values in the selected direction. The lower window shows the variance of the actual projection and the percentage of the total variance that is explained.

Figure 9.1: An arbitrary SLC. MVApcasimu.xpl

Figure 9.2: The most interesting SLC. MVApcasimu.xpl

Figure 9.2 shows the projection that captures the majority of the variance in the data. This direction is of interest and is located along the main direction of the point cloud. The same line of thought can be applied to all data orthogonal to this direction leading to the second eigenvector. The SLC with the highest variance obtained from maximizing (9.2) is the first principal component (PC) $y_1=\gamma_1^{\top} X$. Orthogonal to the direction $\gamma_1$ we find the SLC with the second highest variance: $y_2=\gamma_2^{\top} X$, the second PC.

Proceeding in this way and writing in matrix notation, the result for a random variable $X$ with $E(X)= \mu$ and $\Var(X) = \Sigma =\Gamma\Lambda \Gamma^{\top}$ is the PC transformation which is defined as

$$\undertilde Y = \Gamma^{\top}(\undertilde X-\mu ).$$ (9.3)

Here we have centered the variable $X$ in order to obtain a zero mean PC variable $Y$.

EXAMPLE 9.1   Consider a bivariate normal distribution $N(0,\Sigma)$ with $\Sigma=\left( {\tst 1\atop\tst\rho} {\tst \rho\atop\tst 1} \right)$ and $\rho > 0$ (see Example 3.13). Recall that the eigenvalues of this matrix are $\lambda _1=1+\rho$ and $\lambda _2=1-\rho$ with corresponding eigenvectors

$$\gamma _1=\frac{1}{\sqrt{2}}\left( {1 \atop 1 } \right), \qua... ...a _2=\frac{1}{\sqrt{2}}\left( {\phantom{-}1 \atop -1 } \right).$$

The PC transformation is thus

$$\begin{eqnarray*} Y &=& \Gamma^{\top}(X-\mu )=\frac{1}{\sqrt{2}}\left(\begin{arr... ...\left(\begin{array}{c} X_1+X_2 \\ X_1-X_2 \end{array} \right) . \end{eqnarray*}$$

So the first principal component is

$$Y_1=\frac{1 }{ \sqrt 2}(X_1+X_2)$$

and the second is

$$Y_2=\frac{1 }{ \sqrt 2}(X_1-X_2).$$

Let us compute the variances of these PCs using formulas (4.22)-(4.26):

$$\begin{eqnarray*} \mathop{\mathit{Var}}(Y_1) &=& \mathop{\mathit{Var}}\left\{ \f... ...}\\ &=& \frac{1 }{ 2}(1+1+2\rho )=1+\rho \\ &=& \lambda _1. \end{eqnarray*}$$

Similarly we find that

$$\mathop{\mathit{Var}}(Y_2) = \lambda _2.$$

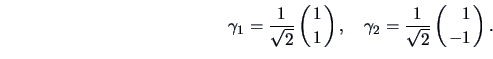
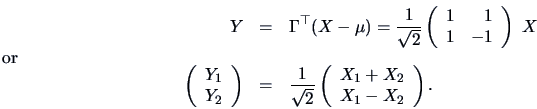
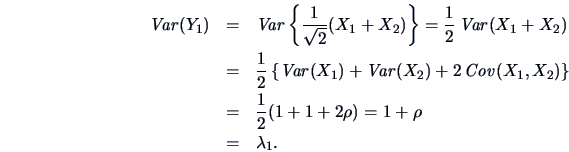
This can be expressed more generally and is given in the next theorem.

THEOREM 9.1   For a given $X\sim(\mu,\Sigma)$ let $Y = \Gamma^{\top}(X-\mu )$ be the PC transformation. Then

$$EY_j=0,\quad j = 1,\ldots ,p$$ (9.4)

$$\mathop{\mathit{Var}}(Y_j)= \lambda _j,\qquad \quad j=1,\ldots ,p$$ (9.5)

$$\mathop{\mathit{Cov}}(Y_i,Y_j) = 0, \qquad i\neq j$$ (9.6)

$$\mathop{\mathit{Var}}(Y_1)\ge \mathop{\mathit{Var}}(Y_2)\ge \cdots\ge\mathop{\mathit{Var}}(Y_p)\ge 0$$ (9.7)

$$\sum ^p_{j=1}\mathop{\mathit{Var}}(Y_j)=\mathop{\hbox{tr}}(\Sigma )$$ (9.8)

$$\prod ^p_{j=1}\mathop{\mathit{Var}}(Y_j)=\vert\Sigma \vert.$$ (9.9)

The connection between the PC transformation and the search for the best SLC is made in the following theorem, which follows directly from (9.2) and Theorem 2.5.

THEOREM 9.2   There exists no SLC that has larger variance than $\lambda _1=\mathop{\mathit{Var}}(Y_1)$.

THEOREM 9.3   If $Y =a^{\top}X$ is a SLC that is not correlated with the first $k$ PCs of $X$, then the variance of $Y$ is maximized by choosing it to be the $(k+1)$-st PC.

Summary

$\ast$

A standardized linear combination (SLC) is a weighted average $\delta^{\top}X=\sum_{j=1}^p \delta_{j} X_{j}$ where $\delta$ is a vector of length $1$.

$\ast$

Maximizing the variance of $\delta^{\top}X$ leads to the choice $\delta=\gamma_{1}$, the eigenvector corresponding to the largest eigenvalue $\lambda_{1}$ of $\Sigma=\Var(X)$.
This is a projection of $X$ into the one-dimensional space, where the components of $X$ are weighted by the elements of $\gamma_{1}$. $Y_{1}=\gamma_{1}^{\top}(X-\mu)$
is called the first principal component (PC).

$\ast$

This projection can be generalized for higher dimensions. The PC transformation is the linear transformation $Y = \Gamma^{\top}(X-\mu )$, where $\Sigma=\Var(X)=\Gamma\Lambda\Gamma^{\top}$ and $\mu=E X$.
$Y_{1},Y_{2}, \ldots ,Y_{p}$ are called the first, second,..., and $p$-th PCs.

$\ast$

The PCs have zero means, variance $\mathop{\mathit{Var}}(Y_{j})=\lambda_{j}$, and zero covariances. From $\lambda_{1}\ge\ldots\ge\lambda_{p}$ it follows that $\mathop{\mathit{Var}}(Y_{1})\ge\ldots\ge\mathop{\mathit{Var}}(Y_{p})$. It holds that $\sum ^p_{j=1}\mathop{\mathit{Var}}(Y_j)=\mathop{\hbox{tr}}(\Sigma )$ and $\prod ^p_{j=1}\mathop{\mathit{Var}}(Y_j)=\vert\Sigma \vert$.

$\ast$

If $Y =a^{\top}X$ is a SLC which is not correlated with the first $k$ PCs of $X$ then the variance of $Y$ is maximized by choosing it to be the $(k+1)$-st PC.